Para calcular el área de un triángulo necesita saber su altura. Para encontrar la altura, siga estas instrucciones. Al menos debe tener una base para encontrar la altura.
Método uno de tres:
Usar la base y el área para encontrar la altura
-
 1 Recuerde la fórmula para el área de un triángulo. La fórmula para el área de un triángulo es A = 1 / 2bh. [1]
1 Recuerde la fórmula para el área de un triángulo. La fórmula para el área de un triángulo es A = 1 / 2bh. [1] - UN = Área del triángulo
- segundo = Longitud de la base del triángulo
- h = Altura de la base del triángulo
-
 2 Mire su triángulo y determine qué variables conoce. Usted ya conoce el área, así que asigne ese valor a UN. También debe conocer el valor de una longitud lateral; asigne ese valor a "'b'". Cualquier lado de un triángulo puede ser la base, independientemente de cómo se dibuje el triángulo. Para visualizar esto, solo imagine girar el triángulo hasta que la longitud del lado conocido esté en la parte inferior. Ejemplo
2 Mire su triángulo y determine qué variables conoce. Usted ya conoce el área, así que asigne ese valor a UN. También debe conocer el valor de una longitud lateral; asigne ese valor a "'b'". Cualquier lado de un triángulo puede ser la base, independientemente de cómo se dibuje el triángulo. Para visualizar esto, solo imagine girar el triángulo hasta que la longitud del lado conocido esté en la parte inferior. Ejemplo
Si sabes que el área de un triángulo es 20, y un lado es 4, entonces:
A = 20 y b = 4.
-
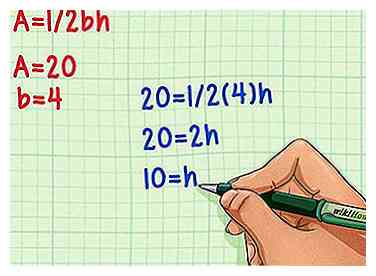 3 Enchufe sus valores en la ecuación A = 1 / 2bh y haz los cálculos. Primero, multiplique la base (b) por 1/2, luego divida el área (A) por el producto. ¡El valor resultante será la altura de tu triángulo! Ejemplo
3 Enchufe sus valores en la ecuación A = 1 / 2bh y haz los cálculos. Primero, multiplique la base (b) por 1/2, luego divida el área (A) por el producto. ¡El valor resultante será la altura de tu triángulo! Ejemplo
20 = 1/2 (4) h Enchufe los números en la ecuación.
20 = 2h Multiplica 4 por 1/2.
10 = h Divide por 2 para encontrar el valor de altura.
Método dos de tres:
Encontrar la altura de un triángulo equilátero
-
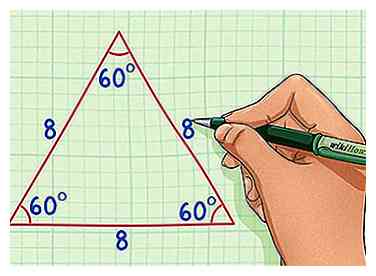 1 Recuerde las propiedades de un triángulo equilátero. Un triángulo equilátero tiene tres lados iguales y tres ángulos iguales cada uno de 60 grados. Si cortas un triángulo equilátero por la mitad, terminarás con dos triángulos rectángulos congruentes. [2]
1 Recuerde las propiedades de un triángulo equilátero. Un triángulo equilátero tiene tres lados iguales y tres ángulos iguales cada uno de 60 grados. Si cortas un triángulo equilátero por la mitad, terminarás con dos triángulos rectángulos congruentes. [2] - En este ejemplo, utilizaremos un triángulo equilátero con longitudes laterales de 8.
-
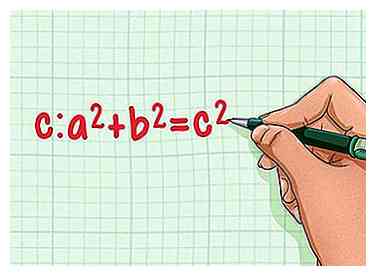 2 Recuerda el teorema de Pitágoras. El teorema de Pitágoras establece que para cualquier triángulo rectángulo con lados de longitud un y segundoy hipotenusa de longitud do: un2 + b2 = c2. ¡Podemos usar este teorema para encontrar la altura de nuestro triángulo equilátero![3]
2 Recuerda el teorema de Pitágoras. El teorema de Pitágoras establece que para cualquier triángulo rectángulo con lados de longitud un y segundoy hipotenusa de longitud do: un2 + b2 = c2. ¡Podemos usar este teorema para encontrar la altura de nuestro triángulo equilátero![3] -
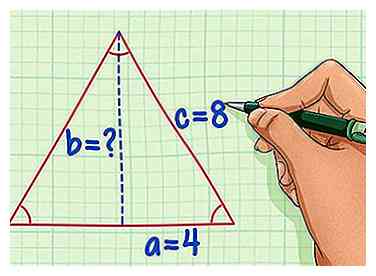 3 Rompe el triángulo equilátero por la mitad y asigna valores a las variables un, segundoy do. La hipotenusa do será igual a la longitud del lado original. Lado un será igual a 1/2 de la longitud lateral, y lateral segundo es la altura del triángulo que tenemos que resolver.
3 Rompe el triángulo equilátero por la mitad y asigna valores a las variables un, segundoy do. La hipotenusa do será igual a la longitud del lado original. Lado un será igual a 1/2 de la longitud lateral, y lateral segundo es la altura del triángulo que tenemos que resolver. - Usando nuestro ejemplo de triángulo equilátero con lados de 8, c = 8 y a = 4.
-
 4 Enchufe los valores en el Teorema de Pitágoras y resuelva para b2. Primer cuadrado do y un al multiplicar cada número por sí mismo. Luego resta una2 desde C2. Ejemplo
4 Enchufe los valores en el Teorema de Pitágoras y resuelva para b2. Primer cuadrado do y un al multiplicar cada número por sí mismo. Luego resta una2 desde C2. Ejemplo
42 + b2 = 82 Enchufe los valores para a y c.
16 + b2 = 64 Cuadrado ay c.
segundo2 = 48 Reste un2 desde C2.
-
 5 Encuentra la raíz cuadrada de b2 para obtener la altura de tu triángulo! Usa la función de raíz cuadrada en tu calculadora para encontrar Sqrt (2. ¡La respuesta es la altura de tu triángulo equilátero!
5 Encuentra la raíz cuadrada de b2 para obtener la altura de tu triángulo! Usa la función de raíz cuadrada en tu calculadora para encontrar Sqrt (2. ¡La respuesta es la altura de tu triángulo equilátero! - b = Sqrt (48) = 6.93
Método tres de tres:
Determinación de la altura con ángulos y lados
-
 1 Determine qué variables conoce. La altura de un triángulo se puede encontrar si tiene 2 lados y el ángulo entre ellos, o los tres lados. Llamaremos a los lados del triángulo a, b, y c, y los ángulos, A, B y C.
1 Determine qué variables conoce. La altura de un triángulo se puede encontrar si tiene 2 lados y el ángulo entre ellos, o los tres lados. Llamaremos a los lados del triángulo a, b, y c, y los ángulos, A, B y C. - Si tiene los tres lados, usará la fórmula de Heron y la fórmula para el área de un triángulo.
- Si tiene dos lados y un ángulo, usará la fórmula para el área dada con dos ángulos y un lado. A = 1 / 2ab (sin C).[4]
-
 2 Usa la fórmula de Heron si tienes los tres lados. La fórmula de Heron tiene dos partes. Primero, debes encontrar la variable s, que es igual a la mitad del perímetro del triángulo. Esto se hace con esta fórmula: s = (a + b + c) / 2.[5] Ejemplo de fórmula de Heron
2 Usa la fórmula de Heron si tienes los tres lados. La fórmula de Heron tiene dos partes. Primero, debes encontrar la variable s, que es igual a la mitad del perímetro del triángulo. Esto se hace con esta fórmula: s = (a + b + c) / 2.[5] Ejemplo de fórmula de Heron
Para un triángulo con lados a = 4, b = 3 yc = 5:
s = (4 + 3 + 5) / 2
s = (12) / 2
s = 6
Luego usa la segunda parte de la fórmula de Heron, Área = sqr (s (s-a) (s-b) (s-c). Reemplaza el área en la ecuación con su equivalente en la fórmula del área: 1 / 2bh (o 1 / 2ah o 1 / 2ch).
Resuelve para h. Para nuestro ejemplo de triángulo, esto se ve así:
1/2 (3) h = sqr (6 (6-4) (6-3) (6-5).
3 / 2h = sqr (6 (2) (3) (1)
3 / 2h = sqr (36)
Usa una calculadora para calcular la raíz cuadrada, que en este caso lo hace 3 / 2h = 6.
Por lo tanto, la altura es igual a 4, usando el lado b como base.
-
 3 Usa el área de dos lados y una fórmula de ángulo si tienes un lado y un ángulo. Reemplace el área en la fórmula con su equivalente en el área de una fórmula triangular: 1 / 2bh. Esto le da una fórmula que se ve como 1 / 2bh = 1 / 2ab (sin C). Esto se puede simplificar a h = a (sen C), eliminando así una de las variables laterales.[6] Encontrar altura con 1 lado y 1 ángulo de ejemplo
3 Usa el área de dos lados y una fórmula de ángulo si tienes un lado y un ángulo. Reemplace el área en la fórmula con su equivalente en el área de una fórmula triangular: 1 / 2bh. Esto le da una fórmula que se ve como 1 / 2bh = 1 / 2ab (sin C). Esto se puede simplificar a h = a (sen C), eliminando así una de las variables laterales.[6] Encontrar altura con 1 lado y 1 ángulo de ejemplo
Por ejemplo, con a = 3 y C = 40 grados, la ecuación se ve así:
h = 3 (sen 40)
Usa tu calculadora para terminar la ecuación, lo que hace h aproximadamente 1.928.
 Minotauromaquia
Minotauromaquia
 1 Recuerde la fórmula para el área de un triángulo. La fórmula para el área de un triángulo es A = 1 / 2bh. [1]
1 Recuerde la fórmula para el área de un triángulo. La fórmula para el área de un triángulo es A = 1 / 2bh. [1]  2 Mire su triángulo y determine qué variables conoce. Usted ya conoce el área, así que asigne ese valor a UN. También debe conocer el valor de una longitud lateral; asigne ese valor a "'b'". Cualquier lado de un triángulo puede ser la base, independientemente de cómo se dibuje el triángulo. Para visualizar esto, solo imagine girar el triángulo hasta que la longitud del lado conocido esté en la parte inferior.
2 Mire su triángulo y determine qué variables conoce. Usted ya conoce el área, así que asigne ese valor a UN. También debe conocer el valor de una longitud lateral; asigne ese valor a "'b'". Cualquier lado de un triángulo puede ser la base, independientemente de cómo se dibuje el triángulo. Para visualizar esto, solo imagine girar el triángulo hasta que la longitud del lado conocido esté en la parte inferior. 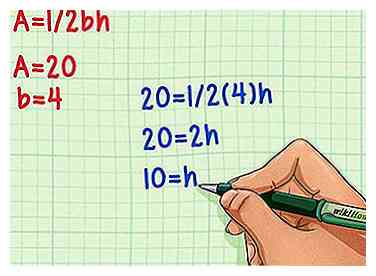 3 Enchufe sus valores en la ecuación A = 1 / 2bh y haz los cálculos. Primero, multiplique la base (b) por 1/2, luego divida el área (A) por el producto. ¡El valor resultante será la altura de tu triángulo!
3 Enchufe sus valores en la ecuación A = 1 / 2bh y haz los cálculos. Primero, multiplique la base (b) por 1/2, luego divida el área (A) por el producto. ¡El valor resultante será la altura de tu triángulo!  1 Recuerde las propiedades de un triángulo equilátero. Un triángulo equilátero tiene tres lados iguales y tres ángulos iguales cada uno de 60 grados. Si cortas un triángulo equilátero por la mitad, terminarás con dos triángulos rectángulos congruentes. [2]
1 Recuerde las propiedades de un triángulo equilátero. Un triángulo equilátero tiene tres lados iguales y tres ángulos iguales cada uno de 60 grados. Si cortas un triángulo equilátero por la mitad, terminarás con dos triángulos rectángulos congruentes. [2] 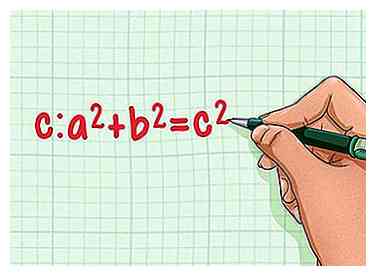 2 Recuerda el teorema de Pitágoras. El teorema de Pitágoras establece que para cualquier triángulo rectángulo con lados de longitud un y segundoy hipotenusa de longitud do: un2 + b2 = c2. ¡Podemos usar este teorema para encontrar la altura de nuestro triángulo equilátero![3]
2 Recuerda el teorema de Pitágoras. El teorema de Pitágoras establece que para cualquier triángulo rectángulo con lados de longitud un y segundoy hipotenusa de longitud do: un2 + b2 = c2. ¡Podemos usar este teorema para encontrar la altura de nuestro triángulo equilátero![3]  3 Rompe el triángulo equilátero por la mitad y asigna valores a las variables un, segundoy do. La hipotenusa do será igual a la longitud del lado original. Lado un será igual a 1/2 de la longitud lateral, y lateral segundo es la altura del triángulo que tenemos que resolver.
3 Rompe el triángulo equilátero por la mitad y asigna valores a las variables un, segundoy do. La hipotenusa do será igual a la longitud del lado original. Lado un será igual a 1/2 de la longitud lateral, y lateral segundo es la altura del triángulo que tenemos que resolver.  4 Enchufe los valores en el Teorema de Pitágoras y resuelva para b2. Primer cuadrado do y un al multiplicar cada número por sí mismo. Luego resta una2 desde C2.
4 Enchufe los valores en el Teorema de Pitágoras y resuelva para b2. Primer cuadrado do y un al multiplicar cada número por sí mismo. Luego resta una2 desde C2.  5 Encuentra la raíz cuadrada de b2 para obtener la altura de tu triángulo! Usa la función de raíz cuadrada en tu calculadora para encontrar Sqrt (2. ¡La respuesta es la altura de tu triángulo equilátero!
5 Encuentra la raíz cuadrada de b2 para obtener la altura de tu triángulo! Usa la función de raíz cuadrada en tu calculadora para encontrar Sqrt (2. ¡La respuesta es la altura de tu triángulo equilátero!  1 Determine qué variables conoce. La altura de un triángulo se puede encontrar si tiene 2 lados y el ángulo entre ellos, o los tres lados. Llamaremos a los lados del triángulo a, b, y c, y los ángulos, A, B y C.
1 Determine qué variables conoce. La altura de un triángulo se puede encontrar si tiene 2 lados y el ángulo entre ellos, o los tres lados. Llamaremos a los lados del triángulo a, b, y c, y los ángulos, A, B y C.  2 Usa la fórmula de Heron si tienes los tres lados. La fórmula de Heron tiene dos partes. Primero, debes encontrar la variable s, que es igual a la mitad del perímetro del triángulo. Esto se hace con esta fórmula: s = (a + b + c) / 2.[5]
2 Usa la fórmula de Heron si tienes los tres lados. La fórmula de Heron tiene dos partes. Primero, debes encontrar la variable s, que es igual a la mitad del perímetro del triángulo. Esto se hace con esta fórmula: s = (a + b + c) / 2.[5]  3 Usa el área de dos lados y una fórmula de ángulo si tienes un lado y un ángulo. Reemplace el área en la fórmula con su equivalente en el área de una fórmula triangular: 1 / 2bh. Esto le da una fórmula que se ve como 1 / 2bh = 1 / 2ab (sin C). Esto se puede simplificar a h = a (sen C), eliminando así una de las variables laterales.[6]
3 Usa el área de dos lados y una fórmula de ángulo si tienes un lado y un ángulo. Reemplace el área en la fórmula con su equivalente en el área de una fórmula triangular: 1 / 2bh. Esto le da una fórmula que se ve como 1 / 2bh = 1 / 2ab (sin C). Esto se puede simplificar a h = a (sen C), eliminando así una de las variables laterales.[6]