En geometría, el término "perímetro" generalmente se refiere al distancia total alrededor del exterior de un polígono, una forma bidimensional de 3 o más lados y ángulos. En otras palabras, el perímetro de una forma dada es la suma de las longitudes de todos sus lados. La facilidad con la que se puede encontrar el perímetro de una forma depende de varios factores, a saber, si el polígono es un regular polígono (un polígono cuyos lados y ángulos son todos iguales) y, si no, si todas las longitudes de los lados en la forma son conocidas. Si ninguna de estas condiciones es verdadera, la dificultad de encontrar el perímetro de la forma depende de cuánta información se conozca sobre la forma.
Pasos
-
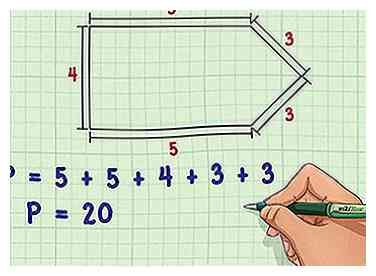 1 Encuentra y agrega las longitudes de todos los lados del polígono. El perímetro de alguna El polígono se puede calcular encontrando la longitud de cada lado individualmente, luego sumando todas estas longitudes juntas. Esta es la forma más directa de encontrar el perímetro de un polígono y, en las formas en las que no hay dos lados iguales, suele ser la única forma precisa de hacerlo.
1 Encuentra y agrega las longitudes de todos los lados del polígono. El perímetro de alguna El polígono se puede calcular encontrando la longitud de cada lado individualmente, luego sumando todas estas longitudes juntas. Esta es la forma más directa de encontrar el perímetro de un polígono y, en las formas en las que no hay dos lados iguales, suele ser la única forma precisa de hacerlo. - Como ejemplo simple, un polígono irregular con longitudes laterales de 5, 5, 4, 3 y 3 tendría un perímetro de 5 + 5 + 4 + 3 + 3 = 20
- Si se desconoce uno o más de los lados de su polígono, el proceso de cálculo del perímetro puede ser difícil y puede requerir un conocimiento más avanzado de la geometría. Por ejemplo, si su polígono es un triángulo rectángulo (o puede dividirse en triángulos rectos, la trigonometría puede ser una herramienta útil para encontrar las longitudes de lados desconocidos que le impiden encontrar el perímetro de la forma en sí.
-
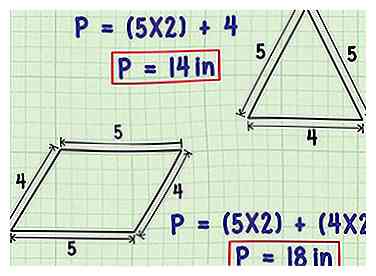 2 Multiplique las longitudes de lados iguales por el número de lados iguales. Ciertos tipos de polígonos tienen dos o más lados iguales. Por ejemplo, los triángulos isósceles y los trapecios isósceles tienen 2 de los lados de la misma longitud, mientras que los paralelogramos y rectángulos tienen 2 pares de lados opuestos con la misma longitud. En estos casos, si conoce la longitud de uno de los lados idénticos, puede multiplicar esta longitud por el número de lados que comparten esta longitud, luego agregue las longitudes de los lados desiguales para encontrar el perímetro de la forma general.
2 Multiplique las longitudes de lados iguales por el número de lados iguales. Ciertos tipos de polígonos tienen dos o más lados iguales. Por ejemplo, los triángulos isósceles y los trapecios isósceles tienen 2 de los lados de la misma longitud, mientras que los paralelogramos y rectángulos tienen 2 pares de lados opuestos con la misma longitud. En estos casos, si conoce la longitud de uno de los lados idénticos, puede multiplicar esta longitud por el número de lados que comparten esta longitud, luego agregue las longitudes de los lados desiguales para encontrar el perímetro de la forma general. - Por ejemplo, consideremos un triángulo isósceles que tiene dos lados con una longitud de 5 pulgadas (12.7 cm) y un lado con una longitud de 4 pulgadas (10.2 cm). Aquí, para encontrar el perímetro, tomamos la longitud de los lados iguales (5) y la multiplicamos por el número de lados iguales (2), luego agregamos las longitudes del lado desigual restante. (5 × 2) + 4 = 10 + 4 = 14 pulgadas (35.6 cm).
- Como ejemplo de una forma con múltiples pares de lados iguales, consideremos un paralelogramo con 2 lados con una longitud de 5 pulgadas (12.7 cm) y 2 con una longitud de 4. Para encontrar el perímetro, multiplicaríamos la longitud del lado más largo por 2 y la longitud del lado más corto, luego agregue los productos juntos. (2 × 5) + (2 × 4) = 10 + 8 = 18 pulgadas (45,7 cm).
- Tenga en cuenta que este método también se puede utilizar para cuadrados y rombos, que, junto con los rectángulos, son casos especiales de paralelogramos.
-
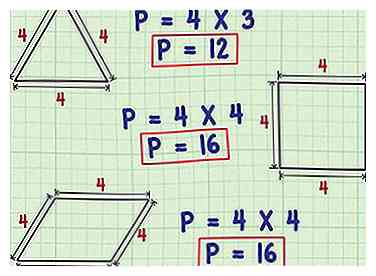 3 Multiplique la longitud del lado de un polígono regular por el número de lados. Polígonos cuyos lados son todas de igual longitud y cuyos ángulos son todas el mismo tamaño se llaman polígonos regulares. Por ejemplo, los cuadrados y triángulos equiláteros son polígonos regulares, al igual que los pentágonos perfectos (como se ejemplifica con el logotipo de Chrysler) y los octágonos (como se ejemplifica con los signos de alto). Si una forma es un polígono regular, encontrar su perímetro es una simple cuestión de multiplicar la longitud de un lado por el número de lados en la forma.
3 Multiplique la longitud del lado de un polígono regular por el número de lados. Polígonos cuyos lados son todas de igual longitud y cuyos ángulos son todas el mismo tamaño se llaman polígonos regulares. Por ejemplo, los cuadrados y triángulos equiláteros son polígonos regulares, al igual que los pentágonos perfectos (como se ejemplifica con el logotipo de Chrysler) y los octágonos (como se ejemplifica con los signos de alto). Si una forma es un polígono regular, encontrar su perímetro es una simple cuestión de multiplicar la longitud de un lado por el número de lados en la forma. - Por ejemplo, el perímetro de un cuadrado perfecto con una longitud lateral de 4 pulgadas (10,2 cm) es 4 × 4 (porque un cuadrado tiene 4 lados), o 16 pulgadas (40.6 cm), mientras que el perímetro de un triángulo equilátero con una longitud lateral de 4 pulgadas (10.2 cm) es 4 × 3, o 12 pulgadas (30.5 cm).
- Este mismo proceso básico también funciona para polígonos no regulares cuyos lados tienen la misma longitud. Por ejemplo, aunque un rombo no es un polígono regular porque sus ángulos no son todos del mismo tamaño, puedes encontrar su perímetro multiplicando la longitud de un lado por el número de lados porque los 4 lados tienen la misma longitud.
-
 4 Alternativamente, use el área y apotema de un polígono regular para encontrar su perímetro. Aunque la forma más sencilla de encontrar su perímetro es simplemente multiplicar la longitud de uno de los lados de un polígono regular por el número de lados del polígono, no es la única manera. La distancia desde el centro del polígono al centro exacto de uno de sus lados, llamado apotema, es parte de una ecuación que le permite encontrar su perímetro, siempre que también conozca el área del polígono. Insertar valores conocidos para área y apotema en la ecuación (Área) = (Perímetro) × (Apothem) / 2 le permite resolver el área del polígono usando álgebra simple.
4 Alternativamente, use el área y apotema de un polígono regular para encontrar su perímetro. Aunque la forma más sencilla de encontrar su perímetro es simplemente multiplicar la longitud de uno de los lados de un polígono regular por el número de lados del polígono, no es la única manera. La distancia desde el centro del polígono al centro exacto de uno de sus lados, llamado apotema, es parte de una ecuación que le permite encontrar su perímetro, siempre que también conozca el área del polígono. Insertar valores conocidos para área y apotema en la ecuación (Área) = (Perímetro) × (Apothem) / 2 le permite resolver el área del polígono usando álgebra simple. - Por ejemplo, el cuadrado con una longitud lateral de 4 pulgadas (10,2 cm) en el ejemplo anterior tiene un área de 16 pulgadas2 y una apotema de 2 pulgadas (5.1 cm). Usando nuestra nueva ecuación, resolvemos para el perímetro de la siguiente manera:
- 16 = (perímetro) × 2/2
- 16 = (perímetro) × 1
- 16 = perímetro. El perímetro del cuadrado es 16 pulgadas (40.6 cm) - Esta es la misma respuesta que obtuvimos arriba con el método estándar.
- Por ejemplo, el cuadrado con una longitud lateral de 4 pulgadas (10,2 cm) en el ejemplo anterior tiene un área de 16 pulgadas2 y una apotema de 2 pulgadas (5.1 cm). Usando nuestra nueva ecuación, resolvemos para el perímetro de la siguiente manera:
 Minotauromaquia
Minotauromaquia
 1 Encuentra y agrega las longitudes de todos los lados del polígono. El perímetro de alguna El polígono se puede calcular encontrando la longitud de cada lado individualmente, luego sumando todas estas longitudes juntas. Esta es la forma más directa de encontrar el perímetro de un polígono y, en las formas en las que no hay dos lados iguales, suele ser la única forma precisa de hacerlo.
1 Encuentra y agrega las longitudes de todos los lados del polígono. El perímetro de alguna El polígono se puede calcular encontrando la longitud de cada lado individualmente, luego sumando todas estas longitudes juntas. Esta es la forma más directa de encontrar el perímetro de un polígono y, en las formas en las que no hay dos lados iguales, suele ser la única forma precisa de hacerlo.  2 Multiplique las longitudes de lados iguales por el número de lados iguales. Ciertos tipos de polígonos tienen dos o más lados iguales. Por ejemplo, los triángulos isósceles y los trapecios isósceles tienen 2 de los lados de la misma longitud, mientras que los paralelogramos y rectángulos tienen 2 pares de lados opuestos con la misma longitud. En estos casos, si conoce la longitud de uno de los lados idénticos, puede multiplicar esta longitud por el número de lados que comparten esta longitud, luego agregue las longitudes de los lados desiguales para encontrar el perímetro de la forma general.
2 Multiplique las longitudes de lados iguales por el número de lados iguales. Ciertos tipos de polígonos tienen dos o más lados iguales. Por ejemplo, los triángulos isósceles y los trapecios isósceles tienen 2 de los lados de la misma longitud, mientras que los paralelogramos y rectángulos tienen 2 pares de lados opuestos con la misma longitud. En estos casos, si conoce la longitud de uno de los lados idénticos, puede multiplicar esta longitud por el número de lados que comparten esta longitud, luego agregue las longitudes de los lados desiguales para encontrar el perímetro de la forma general.  3 Multiplique la longitud del lado de un polígono regular por el número de lados. Polígonos cuyos lados son todas de igual longitud y cuyos ángulos son todas el mismo tamaño se llaman polígonos regulares. Por ejemplo, los cuadrados y triángulos equiláteros son polígonos regulares, al igual que los pentágonos perfectos (como se ejemplifica con el logotipo de Chrysler) y los octágonos (como se ejemplifica con los signos de alto). Si una forma es un polígono regular, encontrar su perímetro es una simple cuestión de multiplicar la longitud de un lado por el número de lados en la forma.
3 Multiplique la longitud del lado de un polígono regular por el número de lados. Polígonos cuyos lados son todas de igual longitud y cuyos ángulos son todas el mismo tamaño se llaman polígonos regulares. Por ejemplo, los cuadrados y triángulos equiláteros son polígonos regulares, al igual que los pentágonos perfectos (como se ejemplifica con el logotipo de Chrysler) y los octágonos (como se ejemplifica con los signos de alto). Si una forma es un polígono regular, encontrar su perímetro es una simple cuestión de multiplicar la longitud de un lado por el número de lados en la forma.  4 Alternativamente, use el área y apotema de un polígono regular para encontrar su perímetro. Aunque la forma más sencilla de encontrar su perímetro es simplemente multiplicar la longitud de uno de los lados de un polígono regular por el número de lados del polígono, no es la única manera. La distancia desde el centro del polígono al centro exacto de uno de sus lados, llamado apotema, es parte de una ecuación que le permite encontrar su perímetro, siempre que también conozca el área del polígono. Insertar valores conocidos para área y apotema en la ecuación (Área) = (Perímetro) × (Apothem) / 2 le permite resolver el área del polígono usando álgebra simple.
4 Alternativamente, use el área y apotema de un polígono regular para encontrar su perímetro. Aunque la forma más sencilla de encontrar su perímetro es simplemente multiplicar la longitud de uno de los lados de un polígono regular por el número de lados del polígono, no es la única manera. La distancia desde el centro del polígono al centro exacto de uno de sus lados, llamado apotema, es parte de una ecuación que le permite encontrar su perímetro, siempre que también conozca el área del polígono. Insertar valores conocidos para área y apotema en la ecuación (Área) = (Perímetro) × (Apothem) / 2 le permite resolver el área del polígono usando álgebra simple.