Este método de multiplicación y división fue utilizado por Descartes y proviene de los "Elementos" de Euclides, Libro VI, Proposición 12. Se basa en triángulos similares. ¡Bien podría ser la forma en que la Madre Naturaleza logra la Multiplicación y la División! Uno imagina que la naturaleza podría crear líneas rectas a través de la emisión de vibraciones rápidas a través de partículas o moléculas apretadas. Vea el artículo Centre a Circle y piense cómo podría funcionar al revés para lograr solo este requisito. Sin embargo, esto es solo una teoría, una posibilidad; La ciencia sabe que la naturaleza logra maravillas matemáticas, como la filotaxis, y patrones de crecimiento muy parecidos a los patrones iterativos fractales, ¡pero aún está debatiendo cómo logra eso! Vale la pena pensar e idear experimentos y pruebas empíricas para probarlo.
Pasos
- Familiarícese con la imagen del concepto básico:
 Triángulos similares
Triángulos similares
Parte uno de tres:
El tutorial
-
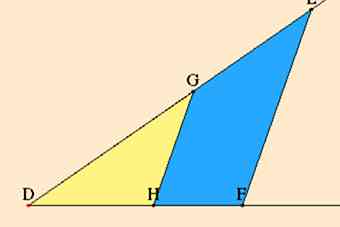
 1 Mire estos triángulos similares, y por lo tanto la proporción DG / DH = DE / DF.
1 Mire estos triángulos similares, y por lo tanto la proporción DG / DH = DE / DF.  Triángulos similares Puedes usarlo para realizar multiplicaciones y divisiones. Abra un nuevo libro de trabajo en Excel y copie el dibujo.
Triángulos similares Puedes usarlo para realizar multiplicaciones y divisiones. Abra un nuevo libro de trabajo en Excel y copie el dibujo. - 2 Para multiplicar x veces y, haga una línea horizontal DH de longitud 1, extienda DF de longitud x desde DH y eleve DG de longitud y en un ángulo por encima de DF horizontal. Dibuje HG y construya una línea a través de F paralela a HG. Deje que cruce DG en E. Entonces, DE tendrá longitud xy.
- 3 Para dividir y por x, haga DH de longitud 1, DF de longitud xy DE de longitud y. Dibuje EF y construya una línea a través de H paralela a EF. Deje que intersecte DE en G. Entonces DG tendrá longitud y / x.
- 4 Supongamos que un tallo u hoja subyacente a otro, en su sombra. ¿Sería posiblemente una forma de mantener el tiempo y "saber cuándo apartarse" para obtener una mejor luz, directamente, para la hoja o el tallo inferior?
- 5 Supongamos que cruzan las raíces (lo que hacen) y suponen cierta sensibilidad entre ellas. ¿Podría ser esta una forma en que las plantas realizan operaciones matemáticas y envían nutrientes vitales de manera oportuna a las plantas? Después de todo, las raíces están en la oscuridad, ¿cómo saben qué hora es o calculan la proporción de una mezcla química dada para enviar?
- 6 Supongamos que las neuronas se bifurcan en varios ángulos en el cerebro (lo que hacen) - podría ser una forma de cálculo de p / n = A.E.N. (Casi cualquier número)? Es decir, casi cualquier número se puede expresar como un cociente de otros dos números, p. 36/2 = 18 y 625/256 = 2.44140625, o 5 ^ 4/4 ^ 4 o 5/4 ^ (1 / (5/4 - 1)). Vea los artículos Comience a Trabajar con Fracciones Continuas y Resuelva aB = a ^ B en Operaciones Neutrales Usando Algebra donde discute E = mc ^ n cuando n se aproxima a 2. ¿Es posible "ver ayer" en la memoria al ver más lento que el Tiempo detenido a la velocidad de la luz al cuadrado? ¿El "Pasado" está en el lado opuesto de todos los electrones y el "Futuro" girando desde esa posición opuesta para saludarme también? Eso haría que el pasado inmediato se pareciera mucho al futuro inmediato, lo que daría como resultado un presente bastante estable. Y geométricamente, todos los rayos de todas las partículas que llegan a través de las vibraciones se multiplicarán y dividirán constantemente, siempre que uno esté bastante quieto o en un entorno relativamente estable. Llame a esto "La suposición sobre las neuronas y los neutrones" si lo desea.
- 7Descartes también usó la siguiente proposición, VI.13, para tomar raíces cuadradas geométricamente.
Parte dos de tres:
Mantente curioso
- 1 Si se puede hacer geométricamente, ¿puede la Madre Naturaleza realizarlo dentro de tolerancias razonables? Es decir, ¿puede obtener estimaciones razonables de la raíz cuadrada o de cualquier raíz de un número? Uno supone "cualquier raíz" desde el supuesto de un proceso iterativo (que aparentemente no le ocurrió a Euclides, Descartes o Newton-Raphson).
- 2 Imagen final:
 Triángulos similares
Triángulos similares
Parte tres de tres:
Orientación útil
- 1 Haga uso de artículos auxiliares cuando proceda a través de este tutorial:
- Para obtener una lista de artículos relacionados con Excel, arte geométrico y / o trigonométrico, gráficos / diagramas y formulación algebraica, vea el artículo Cómo crear una ruta de partículas espirales o una forma de collar o borde esférico.
- Para obtener gráficos y gráficos más artísticos, también puede hacer clic en Categoría: Imágenes de Microsoft Excel, Categoría: Matemáticas, Categoría: Hojas de cálculo o Categoría: Gráficos para ver muchas hojas de cálculo y tablas de Excel donde Trigonometría, Geometría y Cálculo se han convertido en Arte. o simplemente haga clic en la categoría que aparece en la parte superior derecha blanca de esta página, o en la parte inferior izquierda de la página.
 Minotauromaquia
Minotauromaquia

 1 Mire estos triángulos similares, y por lo tanto la proporción DG / DH = DE / DF.
1 Mire estos triángulos similares, y por lo tanto la proporción DG / DH = DE / DF.