Triángulos similares son dos triángulos que tienen los mismos ángulos y lados correspondientes que tienen proporciones iguales.[1] Probar triángulos similares se refiere a un proceso geométrico mediante el cual usted proporciona evidencia para determinar que dos triángulos tienen suficiente en común para ser considerados similares. Usando teoremas geométricos simples, podrá probar fácilmente que dos triángulos son similares.
Parte uno de cuatro:
Usando el teorema de ángulo y ángulo
-
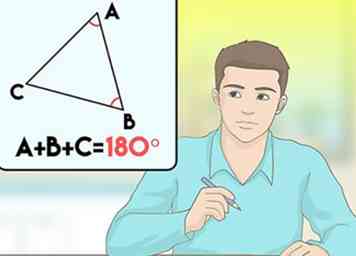 1 Defina el teorema del ángulo-ángulo (AA). Dos triángulos pueden ser probados de manera similar por el teorema de ángulo y ángulo que establece: si dos triángulos tienen dos ángulos congruentes, entonces esos triángulos son similares.
1 Defina el teorema del ángulo-ángulo (AA). Dos triángulos pueden ser probados de manera similar por el teorema de ángulo y ángulo que establece: si dos triángulos tienen dos ángulos congruentes, entonces esos triángulos son similares. - Este teorema también se llama teorema ángulo-ángulo-ángulo (AAA) porque si dos ángulos del triángulo son congruentes, el tercer ángulo también debe ser congruente. Esto se debe a que los ángulos de un triángulo deben sumar 180 °.[2]
-
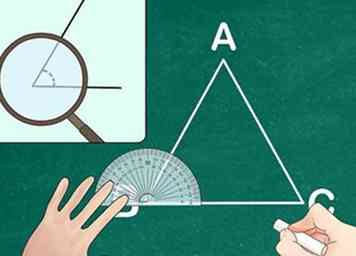 2 Identifica la medida de al menos dos ángulos en uno de los triángulos. Usando un transportador, mida el grado de al menos dos ángulos en el primer triángulo. Rotula los ángulos en el triángulo para hacer un seguimiento de ellos.
2 Identifica la medida de al menos dos ángulos en uno de los triángulos. Usando un transportador, mida el grado de al menos dos ángulos en el primer triángulo. Rotula los ángulos en el triángulo para hacer un seguimiento de ellos. - Elija cualquier dos ángulos en el triángulo para medir.
- Ejemplo: El triángulo ABC tiene dos ángulos que miden 30 ° y 70 °.
-
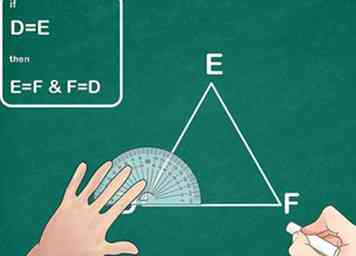 3 Mide al menos dos de los ángulos en el segundo triángulo. Nuevamente, use un transportador para medir dos de los ángulos en el segundo triángulo. Si ambos ángulos son idénticos en ambos triángulos, entonces los triángulos son similares entre sí.
3 Mide al menos dos de los ángulos en el segundo triángulo. Nuevamente, use un transportador para medir dos de los ángulos en el segundo triángulo. Si ambos ángulos son idénticos en ambos triángulos, entonces los triángulos son similares entre sí. - Recuerde, si dos ángulos de un triángulo son iguales, entonces los tres son iguales.
- Ejemplo: El segundo triángulo, DEF, también tiene dos ángulos que miden 30 ° y 70 °.
-
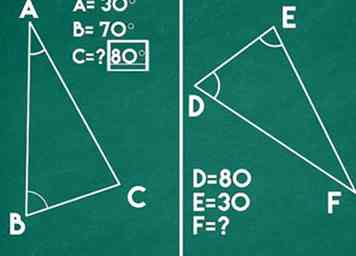 4 Usa el teorema de ángulo-ángulo para similitud. Una vez que haya identificado los ángulos congruentes, puede usar este teorema para demostrar que los triángulos son similares. Establezca que las medidas de los ángulos entre los dos triángulos son idénticas y cite el teorema del ángulo-ángulo como prueba de su similitud.[3]
4 Usa el teorema de ángulo-ángulo para similitud. Una vez que haya identificado los ángulos congruentes, puede usar este teorema para demostrar que los triángulos son similares. Establezca que las medidas de los ángulos entre los dos triángulos son idénticas y cite el teorema del ángulo-ángulo como prueba de su similitud.[3] - Es posible que un triángulo con tres ángulos idénticos también sea congruente, pero también deberían tener longitudes de lados idénticas.
- Ejemplo: Debido a que ambos triángulos tienen dos ángulos idénticos, son similares.
- Nota: si los dos triángulos no tienen ángulos idénticos, no serían similares. Por ejemplo: el triángulo ABC tiene ángulos que miden 30 ° y 70 ° y el triángulo DEF tiene ángulos que miden 35 ° y 70 °. Debido a que 30 ° no es igual a 35 °, los triángulos no son similares.
Parte dos de cuatro:
Usando el teorema del lado del ángulo
-
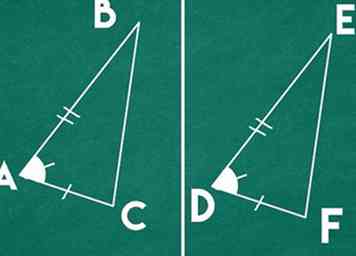 1 Defina el teorema del lado del ángulo (SAS) por similitud. Cuando un triángulo tiene dos lados que están en la misma proporción a otro triángulo y su ángulo incluido es igual, estos triángulos son similares.[4]
1 Defina el teorema del lado del ángulo (SAS) por similitud. Cuando un triángulo tiene dos lados que están en la misma proporción a otro triángulo y su ángulo incluido es igual, estos triángulos son similares.[4] - Tenga cuidado de no confundir este teorema con el teorema del lado del ángulo para congruencia. Para congruencia, los dos lados con su ángulo incluido deben ser idénticos; para similitud, las proporciones de los lados deben ser iguales y el ángulo debe ser idéntico.
- Por ejemplo: triángulo ABC y DEF son similares es el ángulo A = ángulo D y AB / DE = AC / DF.
-
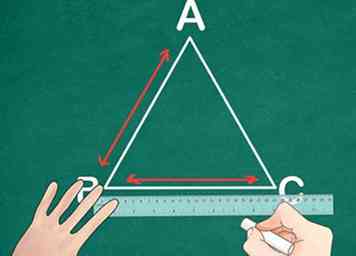 2 Mida los mismos dos lados de cada triángulo. Usando una regla, mida dos lados del triángulo ABC y etiquételos con esa medida. Asegúrese de que el triángulo DEF esté orientado en la misma dirección y mida los mismos dos lados. Etiquete estos lados también.
2 Mida los mismos dos lados de cada triángulo. Usando una regla, mida dos lados del triángulo ABC y etiquételos con esa medida. Asegúrese de que el triángulo DEF esté orientado en la misma dirección y mida los mismos dos lados. Etiquete estos lados también. - Ejemplo: medidas del triángulo ABC; lado AB = 4 cm y lado AC = 8 cm. Medidas del triángulo DEF; lado DE = 2 cm y lado DF = 4 cm.
-
 3 Identifica la medida del ángulo entre esos dos lados. Usando un transportador, mida el ángulo incluido o el ángulo entre los dos lados que ya midió. Para este teorema, la medida del ángulo debe ser idéntica en ambos triángulos.
3 Identifica la medida del ángulo entre esos dos lados. Usando un transportador, mida el ángulo incluido o el ángulo entre los dos lados que ya midió. Para este teorema, la medida del ángulo debe ser idéntica en ambos triángulos. - Ejemplo: el ángulo A en el triángulo ABC es 26 °. El ángulo D en el triángulo DEF también es de 26 °.
-
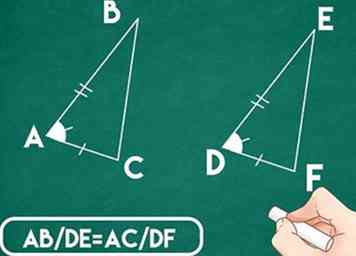 4 Calcule la proporción de las longitudes laterales entre los dos triángulos. Para usar el teorema SAS, los lados de los triángulos deben ser proporcionales entre sí. Para calcular esto, simplemente use la fórmula AB / DE = AC / DF.
4 Calcule la proporción de las longitudes laterales entre los dos triángulos. Para usar el teorema SAS, los lados de los triángulos deben ser proporcionales entre sí. Para calcular esto, simplemente use la fórmula AB / DE = AC / DF. - Ejemplo: AB / DE = AC / DF; 4/2 = 8/4; 2 = 2. Las proporciones de los dos triángulos son iguales.
-
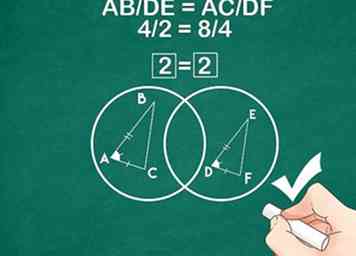 5 Aplica el Teorema del lado del ángulo para demostrar similitud. Una vez que haya determinado que las proporciones de dos lados de un triángulo y su ángulo incluido son iguales, puede usar el teorema SAS en su prueba.
5 Aplica el Teorema del lado del ángulo para demostrar similitud. Una vez que haya determinado que las proporciones de dos lados de un triángulo y su ángulo incluido son iguales, puede usar el teorema SAS en su prueba. - Ejemplo: Debido a que AB / DE = AAC / DF y el ángulo A = ángulo D, el triángulo ABC es similar al triángulo DEF.
- Nota: Si el ángulo A no era igual al ángulo D, los triángulos no serían similares. Además, si las proporciones no fueran iguales, los triángulos no serían similares.
Parte tres de cuatro:
Usando el teorema del lado del lado
-
 1 Defina el teorema del lado del lado (SSS) para la similitud. Dos triángulos se considerarían similares si los tres lados de ambos triángulos son de la misma proporción. Los lados que miden 2: 4: 6 y 4: 8: 12 proporcionarían una prueba de similitud.
1 Defina el teorema del lado del lado (SSS) para la similitud. Dos triángulos se considerarían similares si los tres lados de ambos triángulos son de la misma proporción. Los lados que miden 2: 4: 6 y 4: 8: 12 proporcionarían una prueba de similitud. - Tenga cuidado de no confundir este teorema con el teorema del lado del lado de la congruencia: cuando dos triángulos tienen tres lados idénticos, son congruentes. El teorema de similitud trata estrictamente las proporciones de los tres lados.
- Por ejemplo: en el triángulo ABC y DEF, los triángulos son similares si AB / DE = AC / DF = BC / EF.
-
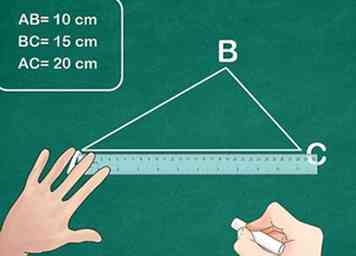 2 Mida los lados de cada triángulo. Usando una regla, mida los tres lados de cada triángulo. Etiquete cada lado para realizar un seguimiento de todas las mediciones. Asegúrese de usar las mismas unidades para cada medición de los lados del triángulo.
2 Mida los lados de cada triángulo. Usando una regla, mida los tres lados de cada triángulo. Etiquete cada lado para realizar un seguimiento de todas las mediciones. Asegúrese de usar las mismas unidades para cada medición de los lados del triángulo. - Ejemplo: el triángulo ABC tiene lados AB = 10 cm, BC = 15 cm, AC = 20 cm y el triángulo DEF tiene lados DE = 2 cm, EF = 3 cm y DF = 4 cm.
-
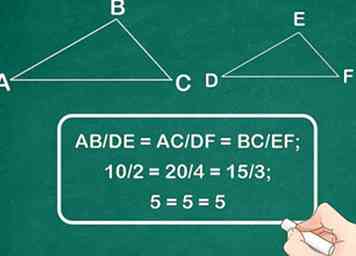 3 Calcula las proporciones entre los lados de cada triángulo. Para que el teorema de SSS sea aplicable, los tres lados de cada triángulo deben ser proporcionales entre sí. Usando las medidas laterales, calcule las proporciones usando la fórmula AB / DE = AC / DF = BC / EF.[5]
3 Calcula las proporciones entre los lados de cada triángulo. Para que el teorema de SSS sea aplicable, los tres lados de cada triángulo deben ser proporcionales entre sí. Usando las medidas laterales, calcule las proporciones usando la fórmula AB / DE = AC / DF = BC / EF.[5] - Ejemplo: AB / DE = AC / DF = BC / EF; 10/2 = 20/4 = 15/3; 5 = 5 = 5.
-
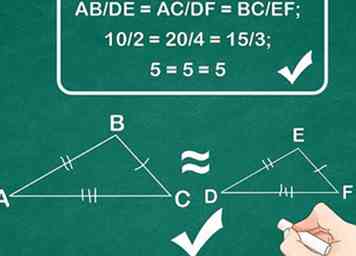 4 Aplica el teorema del lado del costado para probar la similitud. Si ha determinado que las proporciones de los tres lados de los triángulos son iguales entre sí, puede usar el teorema de SSS para demostrar que estos triángulos son similares.[6]
4 Aplica el teorema del lado del costado para probar la similitud. Si ha determinado que las proporciones de los tres lados de los triángulos son iguales entre sí, puede usar el teorema de SSS para demostrar que estos triángulos son similares.[6] - Ejemplo: Debido a que AB / DE = AC / DF = BC / EF, el triángulo ABC y el triángulo DEF son similares.
- Nota: Si AB / DE ≠ AC / DF ≠ BC / EF, entonces los triángulos no serían similares.
Parte cuatro de cuatro:
Escribir una prueba
-
 1 Estudie el formato de una prueba formal. Una prueba comienza con una declaración de información dada que se conoce como la declaración de hipótesis. Tendrá que proporcionar una lista de información relevante, así como evidencia para apoyar cada declaración.
1 Estudie el formato de una prueba formal. Una prueba comienza con una declaración de información dada que se conoce como la declaración de hipótesis. Tendrá que proporcionar una lista de información relevante, así como evidencia para apoyar cada declaración. -
 2 Desarrolle una hipótesis para resolver el problema o complete la prueba. Tendrá que hacer un gráfico, que generalmente tiene dos columnas. Esta primera columna contendrá sus declaraciones, mientras que la segunda proporcionará su evidencia.[7]
2 Desarrolle una hipótesis para resolver el problema o complete la prueba. Tendrá que hacer un gráfico, que generalmente tiene dos columnas. Esta primera columna contendrá sus declaraciones, mientras que la segunda proporcionará su evidencia.[7] - Asegúrese de que la última línea en su columna de extracto siempre coincide con la declaración de la hipótesis. Las filas del medio serán donde muestre su trabajo mientras resuelve el problema. Todas las declaraciones que proporcione, así como su evidencia de respaldo, siempre deben referirse a las cifras que se describen en la declaración de hipótesis.
-
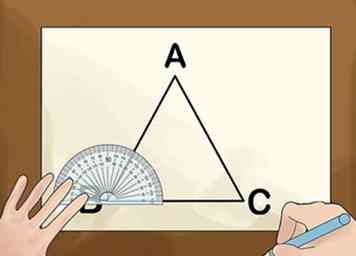 3 Dibuje un diagrama de las figuras que se describen en la hipótesis, si todavía no se ha proporcionado una ilustración. Use todos los detalles que proporciona la hipótesis. Asegúrese de dibujar la figura lo suficientemente grande para que pueda distinguir fácilmente estos detalles. Etiquete todos los puntos que se describen y asegúrese de incluir cualquier información de la declaración con respecto a líneas paralelas o ángulos congruentes.
3 Dibuje un diagrama de las figuras que se describen en la hipótesis, si todavía no se ha proporcionado una ilustración. Use todos los detalles que proporciona la hipótesis. Asegúrese de dibujar la figura lo suficientemente grande para que pueda distinguir fácilmente estos detalles. Etiquete todos los puntos que se describen y asegúrese de incluir cualquier información de la declaración con respecto a líneas paralelas o ángulos congruentes. -
 4 Escriba la información dada. Para cualquier problema, se le dará cierta información sobre las medidas de los ángulos y los lados de los dos triángulos que está tratando de demostrar similar. El primer paso para identificar el teorema correcto es escribir la información que ya conoce.
4 Escriba la información dada. Para cualquier problema, se le dará cierta información sobre las medidas de los ángulos y los lados de los dos triángulos que está tratando de demostrar similar. El primer paso para identificar el teorema correcto es escribir la información que ya conoce. - Si no se proporciona ningún diagrama, dibuje los triángulos y luego etiquete sus ángulos y lados con la información dada.
-
 5 Elija el teorema que se ajuste a la información dada. Una vez que haya anotado la información dada y haya aprendido los tres posibles teoremas que podrían aplicarse, elija el que coincida con la información proporcionada. Está bien si se aplican múltiples teoremas, simplemente elija uno para su prueba.
5 Elija el teorema que se ajuste a la información dada. Una vez que haya anotado la información dada y haya aprendido los tres posibles teoremas que podrían aplicarse, elija el que coincida con la información proporcionada. Está bien si se aplican múltiples teoremas, simplemente elija uno para su prueba. - Si ninguno de estos teoremas concuerda con la información dada, entonces los triángulos no son similares.
-
 6 Escribe la prueba. Diseña una estrategia para resolver la prueba. Hay tres postulados diferentes, o teorías matemáticas, que se aplican a triángulos similares. Cualquiera de estos proporcionará suficiente evidencia para demostrar que los triángulos en cuestión son similares.
6 Escribe la prueba. Diseña una estrategia para resolver la prueba. Hay tres postulados diferentes, o teorías matemáticas, que se aplican a triángulos similares. Cualquiera de estos proporcionará suficiente evidencia para demostrar que los triángulos en cuestión son similares. - Reúna sus datos y teoremas relevantes y escriba la prueba paso a paso.
 Minotauromaquia
Minotauromaquia
 1 Defina el teorema del ángulo-ángulo (AA). Dos triángulos pueden ser probados de manera similar por el teorema de ángulo y ángulo que establece: si dos triángulos tienen dos ángulos congruentes, entonces esos triángulos son similares.
1 Defina el teorema del ángulo-ángulo (AA). Dos triángulos pueden ser probados de manera similar por el teorema de ángulo y ángulo que establece: si dos triángulos tienen dos ángulos congruentes, entonces esos triángulos son similares.  2 Identifica la medida de al menos dos ángulos en uno de los triángulos. Usando un transportador, mida el grado de al menos dos ángulos en el primer triángulo. Rotula los ángulos en el triángulo para hacer un seguimiento de ellos.
2 Identifica la medida de al menos dos ángulos en uno de los triángulos. Usando un transportador, mida el grado de al menos dos ángulos en el primer triángulo. Rotula los ángulos en el triángulo para hacer un seguimiento de ellos.  3 Mide al menos dos de los ángulos en el segundo triángulo. Nuevamente, use un transportador para medir dos de los ángulos en el segundo triángulo. Si ambos ángulos son idénticos en ambos triángulos, entonces los triángulos son similares entre sí.
3 Mide al menos dos de los ángulos en el segundo triángulo. Nuevamente, use un transportador para medir dos de los ángulos en el segundo triángulo. Si ambos ángulos son idénticos en ambos triángulos, entonces los triángulos son similares entre sí.  4 Usa el teorema de ángulo-ángulo para similitud. Una vez que haya identificado los ángulos congruentes, puede usar este teorema para demostrar que los triángulos son similares. Establezca que las medidas de los ángulos entre los dos triángulos son idénticas y cite el teorema del ángulo-ángulo como prueba de su similitud.[3]
4 Usa el teorema de ángulo-ángulo para similitud. Una vez que haya identificado los ángulos congruentes, puede usar este teorema para demostrar que los triángulos son similares. Establezca que las medidas de los ángulos entre los dos triángulos son idénticas y cite el teorema del ángulo-ángulo como prueba de su similitud.[3]  1 Defina el teorema del lado del ángulo (SAS) por similitud. Cuando un triángulo tiene dos lados que están en la misma proporción a otro triángulo y su ángulo incluido es igual, estos triángulos son similares.[4]
1 Defina el teorema del lado del ángulo (SAS) por similitud. Cuando un triángulo tiene dos lados que están en la misma proporción a otro triángulo y su ángulo incluido es igual, estos triángulos son similares.[4]  2 Mida los mismos dos lados de cada triángulo. Usando una regla, mida dos lados del triángulo ABC y etiquételos con esa medida. Asegúrese de que el triángulo DEF esté orientado en la misma dirección y mida los mismos dos lados. Etiquete estos lados también.
2 Mida los mismos dos lados de cada triángulo. Usando una regla, mida dos lados del triángulo ABC y etiquételos con esa medida. Asegúrese de que el triángulo DEF esté orientado en la misma dirección y mida los mismos dos lados. Etiquete estos lados también.  3 Identifica la medida del ángulo entre esos dos lados. Usando un transportador, mida el ángulo incluido o el ángulo entre los dos lados que ya midió. Para este teorema, la medida del ángulo debe ser idéntica en ambos triángulos.
3 Identifica la medida del ángulo entre esos dos lados. Usando un transportador, mida el ángulo incluido o el ángulo entre los dos lados que ya midió. Para este teorema, la medida del ángulo debe ser idéntica en ambos triángulos.  4 Calcule la proporción de las longitudes laterales entre los dos triángulos. Para usar el teorema SAS, los lados de los triángulos deben ser proporcionales entre sí. Para calcular esto, simplemente use la fórmula AB / DE = AC / DF.
4 Calcule la proporción de las longitudes laterales entre los dos triángulos. Para usar el teorema SAS, los lados de los triángulos deben ser proporcionales entre sí. Para calcular esto, simplemente use la fórmula AB / DE = AC / DF.  5 Aplica el Teorema del lado del ángulo para demostrar similitud. Una vez que haya determinado que las proporciones de dos lados de un triángulo y su ángulo incluido son iguales, puede usar el teorema SAS en su prueba.
5 Aplica el Teorema del lado del ángulo para demostrar similitud. Una vez que haya determinado que las proporciones de dos lados de un triángulo y su ángulo incluido son iguales, puede usar el teorema SAS en su prueba.  1 Defina el teorema del lado del lado (SSS) para la similitud. Dos triángulos se considerarían similares si los tres lados de ambos triángulos son de la misma proporción. Los lados que miden 2: 4: 6 y 4: 8: 12 proporcionarían una prueba de similitud.
1 Defina el teorema del lado del lado (SSS) para la similitud. Dos triángulos se considerarían similares si los tres lados de ambos triángulos son de la misma proporción. Los lados que miden 2: 4: 6 y 4: 8: 12 proporcionarían una prueba de similitud.  2 Mida los lados de cada triángulo. Usando una regla, mida los tres lados de cada triángulo. Etiquete cada lado para realizar un seguimiento de todas las mediciones. Asegúrese de usar las mismas unidades para cada medición de los lados del triángulo.
2 Mida los lados de cada triángulo. Usando una regla, mida los tres lados de cada triángulo. Etiquete cada lado para realizar un seguimiento de todas las mediciones. Asegúrese de usar las mismas unidades para cada medición de los lados del triángulo.  3 Calcula las proporciones entre los lados de cada triángulo. Para que el teorema de SSS sea aplicable, los tres lados de cada triángulo deben ser proporcionales entre sí. Usando las medidas laterales, calcule las proporciones usando la fórmula AB / DE = AC / DF = BC / EF.[5]
3 Calcula las proporciones entre los lados de cada triángulo. Para que el teorema de SSS sea aplicable, los tres lados de cada triángulo deben ser proporcionales entre sí. Usando las medidas laterales, calcule las proporciones usando la fórmula AB / DE = AC / DF = BC / EF.[5]  4 Aplica el teorema del lado del costado para probar la similitud. Si ha determinado que las proporciones de los tres lados de los triángulos son iguales entre sí, puede usar el teorema de SSS para demostrar que estos triángulos son similares.[6]
4 Aplica el teorema del lado del costado para probar la similitud. Si ha determinado que las proporciones de los tres lados de los triángulos son iguales entre sí, puede usar el teorema de SSS para demostrar que estos triángulos son similares.[6]  1 Estudie el formato de una prueba formal. Una prueba comienza con una declaración de información dada que se conoce como la declaración de hipótesis. Tendrá que proporcionar una lista de información relevante, así como evidencia para apoyar cada declaración.
1 Estudie el formato de una prueba formal. Una prueba comienza con una declaración de información dada que se conoce como la declaración de hipótesis. Tendrá que proporcionar una lista de información relevante, así como evidencia para apoyar cada declaración.  2 Desarrolle una hipótesis para resolver el problema o complete la prueba. Tendrá que hacer un gráfico, que generalmente tiene dos columnas. Esta primera columna contendrá sus declaraciones, mientras que la segunda proporcionará su evidencia.[7]
2 Desarrolle una hipótesis para resolver el problema o complete la prueba. Tendrá que hacer un gráfico, que generalmente tiene dos columnas. Esta primera columna contendrá sus declaraciones, mientras que la segunda proporcionará su evidencia.[7]  3 Dibuje un diagrama de las figuras que se describen en la hipótesis, si todavía no se ha proporcionado una ilustración. Use todos los detalles que proporciona la hipótesis. Asegúrese de dibujar la figura lo suficientemente grande para que pueda distinguir fácilmente estos detalles. Etiquete todos los puntos que se describen y asegúrese de incluir cualquier información de la declaración con respecto a líneas paralelas o ángulos congruentes.
3 Dibuje un diagrama de las figuras que se describen en la hipótesis, si todavía no se ha proporcionado una ilustración. Use todos los detalles que proporciona la hipótesis. Asegúrese de dibujar la figura lo suficientemente grande para que pueda distinguir fácilmente estos detalles. Etiquete todos los puntos que se describen y asegúrese de incluir cualquier información de la declaración con respecto a líneas paralelas o ángulos congruentes.  4 Escriba la información dada. Para cualquier problema, se le dará cierta información sobre las medidas de los ángulos y los lados de los dos triángulos que está tratando de demostrar similar. El primer paso para identificar el teorema correcto es escribir la información que ya conoce.
4 Escriba la información dada. Para cualquier problema, se le dará cierta información sobre las medidas de los ángulos y los lados de los dos triángulos que está tratando de demostrar similar. El primer paso para identificar el teorema correcto es escribir la información que ya conoce.  5 Elija el teorema que se ajuste a la información dada. Una vez que haya anotado la información dada y haya aprendido los tres posibles teoremas que podrían aplicarse, elija el que coincida con la información proporcionada. Está bien si se aplican múltiples teoremas, simplemente elija uno para su prueba.
5 Elija el teorema que se ajuste a la información dada. Una vez que haya anotado la información dada y haya aprendido los tres posibles teoremas que podrían aplicarse, elija el que coincida con la información proporcionada. Está bien si se aplican múltiples teoremas, simplemente elija uno para su prueba.  6 Escribe la prueba. Diseña una estrategia para resolver la prueba. Hay tres postulados diferentes, o teorías matemáticas, que se aplican a triángulos similares. Cualquiera de estos proporcionará suficiente evidencia para demostrar que los triángulos en cuestión son similares.
6 Escribe la prueba. Diseña una estrategia para resolver la prueba. Hay tres postulados diferentes, o teorías matemáticas, que se aplican a triángulos similares. Cualquiera de estos proporcionará suficiente evidencia para demostrar que los triángulos en cuestión son similares.