El radio de una esfera (abreviado como la variable r o R) es la distancia desde el centro exacto de la esfera a un punto en el borde exterior de esa esfera. Al igual que con los círculos, el radio de una esfera es a menudo una pieza esencial de información de inicio para calcular el diámetro, la circunferencia, el área de superficie y / o el volumen de la forma. Sin embargo, también puede trabajar hacia atrás desde el diámetro, la circunferencia, etc. para encontrar el radio de la esfera. Usa la fórmula que funciona con la información que tienes.
Método uno de tres:
Uso de fórmulas de cálculo de radio
-
 1 Encuentra el radio si conoces el diámetro. El radio es la mitad del diámetro, así que usa la fórmula r = D / 2. Esto es idéntico al método utilizado para calcular el radio de un círculo a partir de su diámetro.[1]
1 Encuentra el radio si conoces el diámetro. El radio es la mitad del diámetro, así que usa la fórmula r = D / 2. Esto es idéntico al método utilizado para calcular el radio de un círculo a partir de su diámetro.[1] - Si tiene una esfera con un diámetro de 16 cm, encuentre el radio dividiendo 16/2 para obtener 8 cm. Si el diámetro es 42, entonces el radio es 21.
-
 2 Encuentra el radio si conoces la circunferencia. Usa la fórmula C / 2π. Como la circunferencia es igual a πD, que es igual a 2πr, dividir la circunferencia por 2π dará el radio.[2]
2 Encuentra el radio si conoces la circunferencia. Usa la fórmula C / 2π. Como la circunferencia es igual a πD, que es igual a 2πr, dividir la circunferencia por 2π dará el radio.[2] - Si tienes una esfera con una circunferencia de 20 m, encuentra el radio dividiendo 20 / 2π = 3.183 m.
- Usa la misma fórmula para convertir el radio y la circunferencia de un círculo.
-
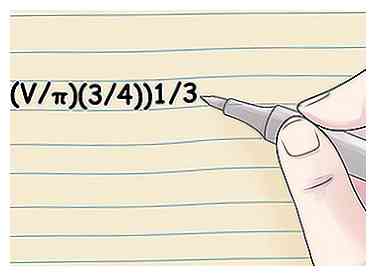 3 Calcula el radio si conoces el volumen de una esfera. Usa la fórmula ((V / π) (3/4))1/3.[3] El volumen de una esfera se deriva de la ecuación V = (4/3) πr3. La solución para la variable r en esta ecuación obtiene ((V / π) (3/4))1/3 = r, lo que significa que el radio de una esfera es igual al volumen dividido por π, multiplicado por 3/4, todos tomados a la potencia de 1/3 (o la raíz cúbica).[4]
3 Calcula el radio si conoces el volumen de una esfera. Usa la fórmula ((V / π) (3/4))1/3.[3] El volumen de una esfera se deriva de la ecuación V = (4/3) πr3. La solución para la variable r en esta ecuación obtiene ((V / π) (3/4))1/3 = r, lo que significa que el radio de una esfera es igual al volumen dividido por π, multiplicado por 3/4, todos tomados a la potencia de 1/3 (o la raíz cúbica).[4] - Si tienes una esfera con un volumen de 100 pulgadas3, resuelve el radio de la siguiente manera:
- ((V / π) (3/4))1/3 = r
- ((100/π)(3/4))1/3 = r
- ((31.83)(3/4))1/3 = r
- (23.87)1/3 = r
- 2.88 in = r
- Si tienes una esfera con un volumen de 100 pulgadas3, resuelve el radio de la siguiente manera:
-
 4 Encuentra el radio del área de la superficie. Usa la fórmula r = √ (A / (4π)). El área de superficie de una esfera se deriva de la ecuación A = 4πr2. La resolución de la variable r arroja √ (A / (4π)) = r, lo que significa que el radio de una esfera es igual a la raíz cuadrada de la superficie dividida por 4π. También puede tomar (A / (4π)) a la potencia 1/2 para el mismo resultado.[5]
4 Encuentra el radio del área de la superficie. Usa la fórmula r = √ (A / (4π)). El área de superficie de una esfera se deriva de la ecuación A = 4πr2. La resolución de la variable r arroja √ (A / (4π)) = r, lo que significa que el radio de una esfera es igual a la raíz cuadrada de la superficie dividida por 4π. También puede tomar (A / (4π)) a la potencia 1/2 para el mismo resultado.[5] - Si tienes una esfera con una superficie de 1,200 cm2, resuelve el radio de la siguiente manera:
- √ (A / (4π)) = r
- √ (1200 / (4π)) = r
- √ (300 / (π)) = r
- √ (95.49) = r
- 9.77 cm = r
- Si tienes una esfera con una superficie de 1,200 cm2, resuelve el radio de la siguiente manera:
Método dos de tres:
Definir conceptos clave
-
 1 Identifica las medidas básicas de una esfera. El radio (r) es la distancia desde el centro exacto de la esfera a cualquier punto en la superficie de la esfera. En términos generales, puede encontrar el radio de una esfera si conoce el diámetro, la circunferencia, el volumen o el área de la superficie.
1 Identifica las medidas básicas de una esfera. El radio (r) es la distancia desde el centro exacto de la esfera a cualquier punto en la superficie de la esfera. En términos generales, puede encontrar el radio de una esfera si conoce el diámetro, la circunferencia, el volumen o el área de la superficie. - Diámetro (D): la distancia a través de la esfera: el doble del radio. El diámetro es la longitud de una línea que atraviesa el centro de la esfera: desde un punto en el exterior de la esfera hasta un punto correspondiente directamente enfrente de él. En otras palabras, la mayor distancia posible entre dos puntos en la esfera.
- Circunferencia (C): la distancia unidimensional alrededor de la esfera en su punto más ancho. En otras palabras, el perímetro de una sección transversal esférica cuyo plano pasa por el centro de la esfera.
- Volumen (V): el espacio tridimensional contenido dentro de la esfera. Es el "espacio que ocupa la esfera".[6]
- Área de superficie (A): el área bidimensional en la superficie exterior de la esfera. La cantidad de espacio plano que cubre el exterior de la esfera.
- Pi (π): una constante que expresa la relación entre la circunferencia del círculo y el diámetro del círculo. Los primeros diez dígitos de Pi son siempre 3.141592653, aunque por lo general se redondea a 3.14.
-
 2 Usa varias medidas para encontrar el radio. Puede usar el diámetro, la circunferencia, el volumen y el área de superficie para calcular el radio de una esfera. También puede calcular cada uno de estos números si conoce la longitud del radio mismo. Por lo tanto, para encontrar el radio, intente invertir las fórmulas para los cálculos de estos componentes. Aprenda las fórmulas que usan el radio para encontrar el diámetro, la circunferencia, el volumen y el área de la superficie.
2 Usa varias medidas para encontrar el radio. Puede usar el diámetro, la circunferencia, el volumen y el área de superficie para calcular el radio de una esfera. También puede calcular cada uno de estos números si conoce la longitud del radio mismo. Por lo tanto, para encontrar el radio, intente invertir las fórmulas para los cálculos de estos componentes. Aprenda las fórmulas que usan el radio para encontrar el diámetro, la circunferencia, el volumen y el área de la superficie. - D = 2r. Al igual que con los círculos, el diámetro de una esfera es el doble del radio.
- C = πD o 2πr. Al igual que con los círculos, la circunferencia de una esfera es igual a π por el diámetro. Dado que el diámetro es dos veces el radio, también podemos decir que la circunferencia es dos veces el radio multiplicado por π.
- V = (4/3) πr3. El volumen de una esfera es el radio en cubos (multiplicado por dos veces), multiplicado por π, multiplicado por 4/3.[7]
- A = 4πr2. El área de superficie de una esfera es el radio al cuadrado (multiplicado por el tiempo), multiplicado por π, multiplicado por 4. Dado que el área de un círculo es πr2, también se puede decir que el área de superficie de una esfera es cuatro veces el área del círculo formado por su circunferencia.
Método tres de tres:
Encontrar el radio como la distancia entre dos puntos
-
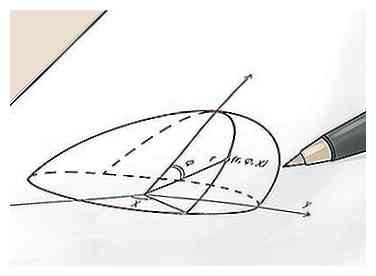 1 Encuentra las coordenadas (x, y, z) del punto central de la esfera. Una forma de pensar en el radio de una esfera es como la distancia entre el punto en el centro de la esfera y cualquier punto en la superficie de la esfera. Como esto es cierto, si conoce las coordenadas del punto en el centro de la esfera y de cualquier punto en la superficie, puede encontrar el radio de la esfera simplemente calculando la distancia entre los dos puntos con una variante de la base fórmula de distancia. Para comenzar, encuentre las coordenadas del punto central de la esfera. Tenga en cuenta que debido a que las esferas son tridimensionales, este será un punto (x, y, z) en lugar de un punto (x, y).
1 Encuentra las coordenadas (x, y, z) del punto central de la esfera. Una forma de pensar en el radio de una esfera es como la distancia entre el punto en el centro de la esfera y cualquier punto en la superficie de la esfera. Como esto es cierto, si conoce las coordenadas del punto en el centro de la esfera y de cualquier punto en la superficie, puede encontrar el radio de la esfera simplemente calculando la distancia entre los dos puntos con una variante de la base fórmula de distancia. Para comenzar, encuentre las coordenadas del punto central de la esfera. Tenga en cuenta que debido a que las esferas son tridimensionales, este será un punto (x, y, z) en lugar de un punto (x, y). - Este proceso es más fácil de entender siguiendo junto con un ejemplo. Para nuestros propósitos, digamos que tenemos una esfera centrada en el punto (x, y, z) (4, -1, 12). En los siguientes pasos, utilizaremos este punto para ayudar a encontrar el radio.
-
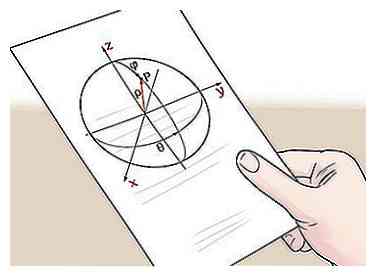 2 Encuentra las coordenadas de un punto en la superficie de la esfera. A continuación, deberá encontrar las coordenadas (x, y, z) de un punto en la superficie de la esfera. Esto puede ser alguna punto en la superficie de la esfera. Debido a que los puntos en la superficie de una esfera son equidistantes del punto central por definición, cualquier punto funcionará para determinar el radio.
2 Encuentra las coordenadas de un punto en la superficie de la esfera. A continuación, deberá encontrar las coordenadas (x, y, z) de un punto en la superficie de la esfera. Esto puede ser alguna punto en la superficie de la esfera. Debido a que los puntos en la superficie de una esfera son equidistantes del punto central por definición, cualquier punto funcionará para determinar el radio. - A los efectos de nuestro problema de ejemplo, digamos que sabemos que el punto (3, 3, 0) se encuentra en la superficie de la esfera. Al calcular la distancia entre este punto y el punto central, podemos encontrar el radio.
-
 3 Encuentra el radio con la fórmula d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). Ahora que conoce el centro de la esfera y un punto en la superficie, al calcular la distancia entre los dos encontrará el radio. Use la fórmula de distancia tridimensional d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2), donde d es igual a la distancia, (x1, y1, z1) es igual a las coordenadas del punto central, y (x2, y2, z2) es igual a las coordenadas del punto en la superficie para encontrar la distancia entre los dos puntos.
3 Encuentra el radio con la fórmula d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). Ahora que conoce el centro de la esfera y un punto en la superficie, al calcular la distancia entre los dos encontrará el radio. Use la fórmula de distancia tridimensional d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2), donde d es igual a la distancia, (x1, y1, z1) es igual a las coordenadas del punto central, y (x2, y2, z2) es igual a las coordenadas del punto en la superficie para encontrar la distancia entre los dos puntos. - En nuestro ejemplo, conectaríamos (4, -1, 12) para (x1, y1, z1) y (3, 3, 0) para (x2, y2, z2), resolviendo de la siguiente manera:
- d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2)
- d = √ ((3 - 4)2 + (3 - -1)2 + (0 - 12)2)
- d = √ ((- 1)2 + (4)2 + (-12)2)
- d = √ (1 + 16 + 144)
- d = √ (161)
- d = 12.69. Este es el radio de nuestra esfera.
- En nuestro ejemplo, conectaríamos (4, -1, 12) para (x1, y1, z1) y (3, 3, 0) para (x2, y2, z2), resolviendo de la siguiente manera:
-
 4 Sepa que, en casos generales, r = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). En una esfera, cada punto en la superficie de la esfera está a la misma distancia del punto central. Si tomamos la fórmula de distancia tridimensional anterior y reemplazamos la variable "d" con la variable "r" por radio, obtenemos una forma de la ecuación que puede encontrar el radio dado a cualquier punto central (x1, y1, z1) y cualquier punto de superficie correspondiente (x2, y2, z2).
4 Sepa que, en casos generales, r = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). En una esfera, cada punto en la superficie de la esfera está a la misma distancia del punto central. Si tomamos la fórmula de distancia tridimensional anterior y reemplazamos la variable "d" con la variable "r" por radio, obtenemos una forma de la ecuación que puede encontrar el radio dado a cualquier punto central (x1, y1, z1) y cualquier punto de superficie correspondiente (x2, y2, z2). - Al cuadrar ambos lados de esta ecuación, obtenemos r2 = (x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2. Tenga en cuenta que esto es esencialmente igual a la ecuación básica de la esfera r2 = x2 + y2 + z2 que asume un punto central de (0,0,0).
 Minotauromaquia
Minotauromaquia
 1 Encuentra el radio si conoces el diámetro. El radio es la mitad del diámetro, así que usa la fórmula r = D / 2. Esto es idéntico al método utilizado para calcular el radio de un círculo a partir de su diámetro.[1]
1 Encuentra el radio si conoces el diámetro. El radio es la mitad del diámetro, así que usa la fórmula r = D / 2. Esto es idéntico al método utilizado para calcular el radio de un círculo a partir de su diámetro.[1]  2 Encuentra el radio si conoces la circunferencia. Usa la fórmula C / 2π. Como la circunferencia es igual a πD, que es igual a 2πr, dividir la circunferencia por 2π dará el radio.[2]
2 Encuentra el radio si conoces la circunferencia. Usa la fórmula C / 2π. Como la circunferencia es igual a πD, que es igual a 2πr, dividir la circunferencia por 2π dará el radio.[2] 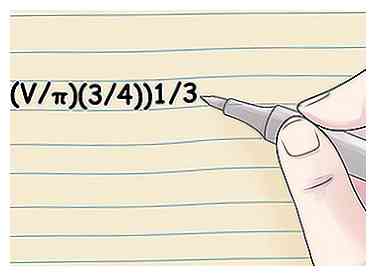 3 Calcula el radio si conoces el volumen de una esfera. Usa la fórmula ((V / π) (3/4))1/3.[3] El volumen de una esfera se deriva de la ecuación V = (4/3) πr3. La solución para la variable r en esta ecuación obtiene ((V / π) (3/4))1/3 = r, lo que significa que el radio de una esfera es igual al volumen dividido por π, multiplicado por 3/4, todos tomados a la potencia de 1/3 (o la raíz cúbica).[4]
3 Calcula el radio si conoces el volumen de una esfera. Usa la fórmula ((V / π) (3/4))1/3.[3] El volumen de una esfera se deriva de la ecuación V = (4/3) πr3. La solución para la variable r en esta ecuación obtiene ((V / π) (3/4))1/3 = r, lo que significa que el radio de una esfera es igual al volumen dividido por π, multiplicado por 3/4, todos tomados a la potencia de 1/3 (o la raíz cúbica).[4]  4 Encuentra el radio del área de la superficie. Usa la fórmula r = √ (A / (4π)). El área de superficie de una esfera se deriva de la ecuación A = 4πr2. La resolución de la variable r arroja √ (A / (4π)) = r, lo que significa que el radio de una esfera es igual a la raíz cuadrada de la superficie dividida por 4π. También puede tomar (A / (4π)) a la potencia 1/2 para el mismo resultado.[5]
4 Encuentra el radio del área de la superficie. Usa la fórmula r = √ (A / (4π)). El área de superficie de una esfera se deriva de la ecuación A = 4πr2. La resolución de la variable r arroja √ (A / (4π)) = r, lo que significa que el radio de una esfera es igual a la raíz cuadrada de la superficie dividida por 4π. También puede tomar (A / (4π)) a la potencia 1/2 para el mismo resultado.[5]  1 Identifica las medidas básicas de una esfera. El radio (r) es la distancia desde el centro exacto de la esfera a cualquier punto en la superficie de la esfera. En términos generales, puede encontrar el radio de una esfera si conoce el diámetro, la circunferencia, el volumen o el área de la superficie.
1 Identifica las medidas básicas de una esfera. El radio (r) es la distancia desde el centro exacto de la esfera a cualquier punto en la superficie de la esfera. En términos generales, puede encontrar el radio de una esfera si conoce el diámetro, la circunferencia, el volumen o el área de la superficie.  2 Usa varias medidas para encontrar el radio. Puede usar el diámetro, la circunferencia, el volumen y el área de superficie para calcular el radio de una esfera. También puede calcular cada uno de estos números si conoce la longitud del radio mismo. Por lo tanto, para encontrar el radio, intente invertir las fórmulas para los cálculos de estos componentes. Aprenda las fórmulas que usan el radio para encontrar el diámetro, la circunferencia, el volumen y el área de la superficie.
2 Usa varias medidas para encontrar el radio. Puede usar el diámetro, la circunferencia, el volumen y el área de superficie para calcular el radio de una esfera. También puede calcular cada uno de estos números si conoce la longitud del radio mismo. Por lo tanto, para encontrar el radio, intente invertir las fórmulas para los cálculos de estos componentes. Aprenda las fórmulas que usan el radio para encontrar el diámetro, la circunferencia, el volumen y el área de la superficie.  1 Encuentra las coordenadas (x, y, z) del punto central de la esfera. Una forma de pensar en el radio de una esfera es como la distancia entre el punto en el centro de la esfera y cualquier punto en la superficie de la esfera. Como esto es cierto, si conoce las coordenadas del punto en el centro de la esfera y de cualquier punto en la superficie, puede encontrar el radio de la esfera simplemente calculando la distancia entre los dos puntos con una variante de la base fórmula de distancia. Para comenzar, encuentre las coordenadas del punto central de la esfera. Tenga en cuenta que debido a que las esferas son tridimensionales, este será un punto (x, y, z) en lugar de un punto (x, y).
1 Encuentra las coordenadas (x, y, z) del punto central de la esfera. Una forma de pensar en el radio de una esfera es como la distancia entre el punto en el centro de la esfera y cualquier punto en la superficie de la esfera. Como esto es cierto, si conoce las coordenadas del punto en el centro de la esfera y de cualquier punto en la superficie, puede encontrar el radio de la esfera simplemente calculando la distancia entre los dos puntos con una variante de la base fórmula de distancia. Para comenzar, encuentre las coordenadas del punto central de la esfera. Tenga en cuenta que debido a que las esferas son tridimensionales, este será un punto (x, y, z) en lugar de un punto (x, y).  2 Encuentra las coordenadas de un punto en la superficie de la esfera. A continuación, deberá encontrar las coordenadas (x, y, z) de un punto en la superficie de la esfera. Esto puede ser alguna punto en la superficie de la esfera. Debido a que los puntos en la superficie de una esfera son equidistantes del punto central por definición, cualquier punto funcionará para determinar el radio.
2 Encuentra las coordenadas de un punto en la superficie de la esfera. A continuación, deberá encontrar las coordenadas (x, y, z) de un punto en la superficie de la esfera. Esto puede ser alguna punto en la superficie de la esfera. Debido a que los puntos en la superficie de una esfera son equidistantes del punto central por definición, cualquier punto funcionará para determinar el radio.  3 Encuentra el radio con la fórmula d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). Ahora que conoce el centro de la esfera y un punto en la superficie, al calcular la distancia entre los dos encontrará el radio. Use la fórmula de distancia tridimensional d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2), donde d es igual a la distancia, (x1, y1, z1) es igual a las coordenadas del punto central, y (x2, y2, z2) es igual a las coordenadas del punto en la superficie para encontrar la distancia entre los dos puntos.
3 Encuentra el radio con la fórmula d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). Ahora que conoce el centro de la esfera y un punto en la superficie, al calcular la distancia entre los dos encontrará el radio. Use la fórmula de distancia tridimensional d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2), donde d es igual a la distancia, (x1, y1, z1) es igual a las coordenadas del punto central, y (x2, y2, z2) es igual a las coordenadas del punto en la superficie para encontrar la distancia entre los dos puntos.  4 Sepa que, en casos generales, r = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). En una esfera, cada punto en la superficie de la esfera está a la misma distancia del punto central. Si tomamos la fórmula de distancia tridimensional anterior y reemplazamos la variable "d" con la variable "r" por radio, obtenemos una forma de la ecuación que puede encontrar el radio dado a cualquier punto central (x1, y1, z1) y cualquier punto de superficie correspondiente (x2, y2, z2).
4 Sepa que, en casos generales, r = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). En una esfera, cada punto en la superficie de la esfera está a la misma distancia del punto central. Si tomamos la fórmula de distancia tridimensional anterior y reemplazamos la variable "d" con la variable "r" por radio, obtenemos una forma de la ecuación que puede encontrar el radio dado a cualquier punto central (x1, y1, z1) y cualquier punto de superficie correspondiente (x2, y2, z2).