Las pruebas matemáticas pueden ser difíciles, pero se pueden conquistar con el conocimiento de fondo adecuado tanto de las matemáticas como del formato de una prueba. Desafortunadamente, no hay una manera rápida y fácil de aprender a construir una prueba. Debe tener una base básica en el tema para llegar a los teoremas y las definiciones adecuadas para diseñar lógicamente su prueba. Al leer ejemplos de pruebas y practicar por su cuenta, podrá cultivar la habilidad de escribir una prueba matemática.
Método uno de tres:
Comprender el problema
-
 1 Identifica la pregunta. Primero debes determinar exactamente qué es lo que intentas probar. Esta pregunta también servirá como la declaración final en la prueba. En este paso, también desea definir las suposiciones con las que trabajará. Identificar la pregunta y las suposiciones necesarias le da un punto de partida para comprender el problema y trabajar la prueba.
1 Identifica la pregunta. Primero debes determinar exactamente qué es lo que intentas probar. Esta pregunta también servirá como la declaración final en la prueba. En este paso, también desea definir las suposiciones con las que trabajará. Identificar la pregunta y las suposiciones necesarias le da un punto de partida para comprender el problema y trabajar la prueba. -
 2 Dibujar diagramas Al intentar comprender el funcionamiento interno de un problema matemático, a veces la forma más fácil es dibujar un diagrama de lo que está sucediendo. Los diagramas son particularmente importantes en las pruebas de geometría, ya que te ayudan a visualizar lo que en realidad estás tratando de probar.
2 Dibujar diagramas Al intentar comprender el funcionamiento interno de un problema matemático, a veces la forma más fácil es dibujar un diagrama de lo que está sucediendo. Los diagramas son particularmente importantes en las pruebas de geometría, ya que te ayudan a visualizar lo que en realidad estás tratando de probar. - Use la información dada en el problema para esbozar un dibujo de la prueba. Etiquete los conocimientos y las incógnitas.
- A medida que trabaje con la prueba, dibuje en la información necesaria que proporciona evidencia para la prueba.
-
 3 Estudie pruebas de teoremas relacionados. Las pruebas son difíciles de aprender a escribir, pero una excelente forma de aprender pruebas es estudiar teoremas relacionados y cómo se probaron.
3 Estudie pruebas de teoremas relacionados. Las pruebas son difíciles de aprender a escribir, pero una excelente forma de aprender pruebas es estudiar teoremas relacionados y cómo se probaron. - Tenga en cuenta que una prueba es solo un buen argumento con cada paso justificado. Puede encontrar muchas pruebas para estudiar en línea o en un libro de texto.[1]
-
 4 Hacer preguntas. Está perfectamente bien quedar atrapado en una prueba. Pregúntele a su maestro o compañeros de clase si tiene preguntas. Pueden tener preguntas similares y pueden resolver los problemas juntos. Es mejor pedir aclaraciones que tropezar a ciegas con la prueba.
4 Hacer preguntas. Está perfectamente bien quedar atrapado en una prueba. Pregúntele a su maestro o compañeros de clase si tiene preguntas. Pueden tener preguntas similares y pueden resolver los problemas juntos. Es mejor pedir aclaraciones que tropezar a ciegas con la prueba. - Reúnase con su maestro fuera de la clase para recibir instrucción adicional.
Método dos de tres:
Formatear una prueba
-
 1 Definir pruebas matemáticas. Una prueba matemática es una serie de enunciados lógicos soportados por teoremas y definiciones que prueban la verdad de otra afirmación matemática.[2] Las pruebas son la única forma de saber que una declaración es matemáticamente válida.
1 Definir pruebas matemáticas. Una prueba matemática es una serie de enunciados lógicos soportados por teoremas y definiciones que prueban la verdad de otra afirmación matemática.[2] Las pruebas son la única forma de saber que una declaración es matemáticamente válida. - Ser capaz de escribir una prueba matemática indica una comprensión fundamental del problema en sí y de todos los conceptos utilizados en el problema.
- Las pruebas también te obligan a mirar las matemáticas de una manera nueva y emocionante. Solo tratando de demostrar algo, obtienes conocimiento y comprensión incluso si tu prueba finalmente no funciona.
-
 2 Conoce a tu audiencia Antes de escribir una prueba, debe pensar en la audiencia para la que está escribiendo y qué información ya conocen. Si está escribiendo una prueba para su publicación, la escribirá de manera diferente a escribir una prueba para su clase de matemáticas de la escuela secundaria.[3]
2 Conoce a tu audiencia Antes de escribir una prueba, debe pensar en la audiencia para la que está escribiendo y qué información ya conocen. Si está escribiendo una prueba para su publicación, la escribirá de manera diferente a escribir una prueba para su clase de matemáticas de la escuela secundaria.[3] - Saber que tu audiencia te permite escribir la prueba de una manera que ellos puedan entender dada la cantidad de conocimiento previo que tienen.
-
 3 Identifica el tipo de prueba que estás escribiendo. Existen diferentes tipos de pruebas y la que elijas depende de tu audiencia y de la tarea asignada. Si no está seguro de qué versión usar, pídale ayuda a su profesor. En la escuela secundaria, se puede esperar que escriba su prueba en un formato específico, como una prueba formal de dos columnas.[4]
3 Identifica el tipo de prueba que estás escribiendo. Existen diferentes tipos de pruebas y la que elijas depende de tu audiencia y de la tarea asignada. Si no está seguro de qué versión usar, pídale ayuda a su profesor. En la escuela secundaria, se puede esperar que escriba su prueba en un formato específico, como una prueba formal de dos columnas.[4] - Una prueba de dos columnas es una configuración que pone datos y declaraciones en una columna y la evidencia de apoyo junto a ella en una segunda columna. Se usan muy comúnmente en geometría.
- Una prueba informal de párrafo usa declaraciones gramaticalmente correctas y menos símbolos. En niveles superiores, siempre debes usar una prueba informal.
-
 4 Escriba la prueba de dos columnas como un bosquejo. La prueba de dos columnas es una manera fácil de organizar tus pensamientos y pensar en el problema. Dibuje una línea en el medio de la página y escriba todos los datos y declaraciones en el lado izquierdo. Escriba las definiciones / teoremas correspondientes en el lado derecho, junto a los datos que respaldan.
4 Escriba la prueba de dos columnas como un bosquejo. La prueba de dos columnas es una manera fácil de organizar tus pensamientos y pensar en el problema. Dibuje una línea en el medio de la página y escriba todos los datos y declaraciones en el lado izquierdo. Escriba las definiciones / teoremas correspondientes en el lado derecho, junto a los datos que respaldan. - Por ejemplo:[5]
- El ángulo A y el ángulo B forman un par lineal. Dado.
- Ángulo ABC es recto. Definición de un ángulo recto.
- El ángulo ABC mide 180 °. Definición de una línea
- Ángulo A + Ángulo B = Ángulo ABC. Postulado de adición de ángulo.
- Ángulo A + Ángulo B = 180 °. Sustitución.
- Ángulo A suplementario a Angle B. Definición de ángulos suplementarios.
- Q.E.D.
-
 5 Convierta la prueba de dos columnas a una prueba escrita informal. Utilizando la prueba de dos columnas como base, escriba la forma informal de párrafo de su prueba sin demasiados símbolos y abreviaturas.
5 Convierta la prueba de dos columnas a una prueba escrita informal. Utilizando la prueba de dos columnas como base, escriba la forma informal de párrafo de su prueba sin demasiados símbolos y abreviaturas. - Por ejemplo: Deje que el ángulo A y el ángulo B sean pares lineales. Por hipótesis, el ángulo A y el ángulo B son suplementarios. El ángulo A y el ángulo B forman una línea recta porque son pares lineales. Una línea recta se define como tener una medida de ángulo de 180 °. Dado el postulado de adición de ángulo, los ángulos A y B se suman para formar la línea ABC. Mediante la sustitución, los ángulos A y B se suman juntos a 180 °, por lo tanto, son ángulos suplementarios. Q.E.D.
Método tres de tres:
Escribiendo la Prueba
-
 1 Aprende el vocabulario de una prueba. Hay ciertas declaraciones y frases que verá una y otra vez en una prueba matemática. Estas son frases con las que debe familiarizarse y saber cómo usarlas correctamente al escribir su propia prueba.[6]
1 Aprende el vocabulario de una prueba. Hay ciertas declaraciones y frases que verá una y otra vez en una prueba matemática. Estas son frases con las que debe familiarizarse y saber cómo usarlas correctamente al escribir su propia prueba.[6] - "Si las declaraciones A, luego B" significan que debes demostrar que A es verdadero, B también debe ser verdadero.[7]
- "A si y solo si B" significa que debes probar que A y B son verdaderos y falsos al mismo tiempo.Demuestre ambos "si A, luego B" y "si no A, entonces no B".
- "A solo si B" es equivalente a "si A, luego B", por lo que no se usa con frecuencia. Aunque es bueno tenerlo en cuenta, en caso de que lo veas.
- Al redactar la prueba, evite usar "I", pero use "nosotros" en su lugar.[8]
-
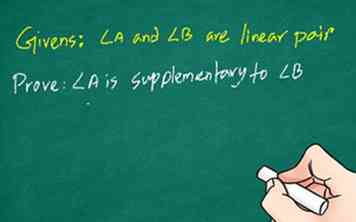 2 Escriba todos los datos. Al redactar una prueba, el primer paso es identificar y anotar todos los datos. Este es el mejor lugar para comenzar porque le ayuda a pensar qué se sabe y qué información necesitará para completar la prueba. Lee el problema y escribe cada uno.
2 Escriba todos los datos. Al redactar una prueba, el primer paso es identificar y anotar todos los datos. Este es el mejor lugar para comenzar porque le ayuda a pensar qué se sabe y qué información necesitará para completar la prueba. Lee el problema y escribe cada uno. - Por ejemplo: demuestre que dos ángulos (ángulo A y ángulo B) que forman un par lineal son suplementarios.[9]
- Givens: ángulo A y ángulo B son un par lineal
- Demostrar: el ángulo A es suplementario al ángulo B
-
 3 Definir todas las variables Además de escribir los datos, es útil definir todas las variables. Escriba las definiciones al comienzo de la prueba para evitar confusiones para el lector. Si las variables no están definidas, un lector puede perderse fácilmente al tratar de comprender su prueba.
3 Definir todas las variables Además de escribir los datos, es útil definir todas las variables. Escriba las definiciones al comienzo de la prueba para evitar confusiones para el lector. Si las variables no están definidas, un lector puede perderse fácilmente al tratar de comprender su prueba. - No use ninguna variable en su prueba que no haya sido definida.
- Por ejemplo: las variables son la medida del ángulo A y la medida del ángulo B.
-
 4 Trabaja con la prueba al revés. A menudo es más fácil pensar en el problema al revés. Comienza con la conclusión, lo que intentas probar, y piensa en los pasos que pueden llevarte al principio.[10]
4 Trabaja con la prueba al revés. A menudo es más fácil pensar en el problema al revés. Comienza con la conclusión, lo que intentas probar, y piensa en los pasos que pueden llevarte al principio.[10] - Manipule los pasos desde el principio hasta el final para ver si puede hacer que se vean unos a otros. Use los datos, las definiciones que ha aprendido y las pruebas que son similares a la que está trabajando.
- Hágase preguntas a medida que avanza. "¿Por qué esto es tan?" y "¿Hay alguna manera de que esto sea falso?" son buenas preguntas para cada declaración o reclamo.
- Recuerde reescribir los pasos en el orden correcto para la prueba final.
- Por ejemplo: si el ángulo A y B son suplementarios, deben sumar 180 °. Los dos ángulos se combinan para formar la línea ABC. Usted sabe que hacen una línea debido a la definición de un par lineal. Como una línea es de 180 °, puede usar la sustitución para demostrar que el ángulo A y el ángulo B suman 180 °.
-
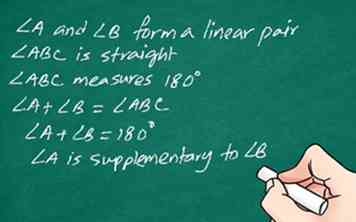 5 Ordene sus pasos lógicamente. Comience la prueba al principio y trabaje hacia la conclusión. Aunque es útil pensar en la prueba comenzando con la conclusión y trabajando hacia atrás, cuando realmente escribes la prueba, indica la conclusión al final.[11] Debe fluir de una declaración a otra, con soporte para cada declaración, de modo que no haya ninguna razón para dudar de la validez de su prueba.
5 Ordene sus pasos lógicamente. Comience la prueba al principio y trabaje hacia la conclusión. Aunque es útil pensar en la prueba comenzando con la conclusión y trabajando hacia atrás, cuando realmente escribes la prueba, indica la conclusión al final.[11] Debe fluir de una declaración a otra, con soporte para cada declaración, de modo que no haya ninguna razón para dudar de la validez de su prueba. - Comience indicando las suposiciones con las que está trabajando.
- Incluya pasos simples y evidentes para que el lector no tenga que preguntarse cómo pasó de un paso a otro.
- Escribir múltiples borradores para sus pruebas no es infrecuente. Siga reorganizando hasta que todos los pasos estén en el orden más lógico.
- Por ejemplo: comience con el comienzo.
- El ángulo A y el ángulo B forman un par lineal.
- Ángulo ABC es recto.
- El ángulo ABC mide 180 °.
- Ángulo A + Ángulo B = Ángulo ABC.
- Ángulo A + Ángulo B = Ángulo 180 °.
- El ángulo A es complementario a Angle B.
-
 6 Evita usar flechas y abreviaturas en la prueba escrita. Cuando diseñe el plan para su prueba, puede usar taquigrafía y símbolos, pero al escribir la prueba final, símbolos como flechas pueden confundir al lector. En su lugar, use palabras como "luego" o "por lo tanto".[12]
6 Evita usar flechas y abreviaturas en la prueba escrita. Cuando diseñe el plan para su prueba, puede usar taquigrafía y símbolos, pero al escribir la prueba final, símbolos como flechas pueden confundir al lector. En su lugar, use palabras como "luego" o "por lo tanto".[12] - Las excepciones al uso de abreviaturas incluyen, p. (por ejemplo) y, es decir, (es decir), pero asegúrese de estar utilizándolos adecuadamente.[13]
-
 7 Admite todas las declaraciones con un teorema, ley o definición. Una prueba es solo tan buena como la evidencia utilizada. No puede hacer una afirmación sin apoyarla con una definición. Consulte otras pruebas similares a la que está trabajando, por ejemplo, evidencia.
7 Admite todas las declaraciones con un teorema, ley o definición. Una prueba es solo tan buena como la evidencia utilizada. No puede hacer una afirmación sin apoyarla con una definición. Consulte otras pruebas similares a la que está trabajando, por ejemplo, evidencia. - Intenta aplicar tu prueba a un caso donde debería fallar, y ver si realmente lo hace. Si no falla, vuelva a trabajar la prueba para que así sea.
- Muchas pruebas geométricas se escriben como una prueba de dos columnas, con la declaración y la evidencia. Una prueba matemática formal para la publicación se escribe como un párrafo con la gramática adecuada.
-
 8 Termine con una conclusión o Q.E.D. La última declaración de la prueba debería ser el concepto que intentabas probar. Una vez que haya hecho esta afirmación, finalice la prueba con un símbolo de conclusión final como Q.E.D. o un cuadrado relleno indica que la prueba está completamente terminada.[14]
8 Termine con una conclusión o Q.E.D. La última declaración de la prueba debería ser el concepto que intentabas probar. Una vez que haya hecho esta afirmación, finalice la prueba con un símbolo de conclusión final como Q.E.D. o un cuadrado relleno indica que la prueba está completamente terminada.[14] - Q.E.D. (quod erat demonstrandum, que en latín significa "que se iba a mostrar").
- Si no está seguro de si su prueba es correcta, solo escriba unas pocas frases que indiquen cuál fue su conclusión y por qué es significativa.
 Minotauromaquia
Minotauromaquia
 1 Identifica la pregunta. Primero debes determinar exactamente qué es lo que intentas probar. Esta pregunta también servirá como la declaración final en la prueba. En este paso, también desea definir las suposiciones con las que trabajará. Identificar la pregunta y las suposiciones necesarias le da un punto de partida para comprender el problema y trabajar la prueba.
1 Identifica la pregunta. Primero debes determinar exactamente qué es lo que intentas probar. Esta pregunta también servirá como la declaración final en la prueba. En este paso, también desea definir las suposiciones con las que trabajará. Identificar la pregunta y las suposiciones necesarias le da un punto de partida para comprender el problema y trabajar la prueba.  2 Dibujar diagramas Al intentar comprender el funcionamiento interno de un problema matemático, a veces la forma más fácil es dibujar un diagrama de lo que está sucediendo. Los diagramas son particularmente importantes en las pruebas de geometría, ya que te ayudan a visualizar lo que en realidad estás tratando de probar.
2 Dibujar diagramas Al intentar comprender el funcionamiento interno de un problema matemático, a veces la forma más fácil es dibujar un diagrama de lo que está sucediendo. Los diagramas son particularmente importantes en las pruebas de geometría, ya que te ayudan a visualizar lo que en realidad estás tratando de probar.  3 Estudie pruebas de teoremas relacionados. Las pruebas son difíciles de aprender a escribir, pero una excelente forma de aprender pruebas es estudiar teoremas relacionados y cómo se probaron.
3 Estudie pruebas de teoremas relacionados. Las pruebas son difíciles de aprender a escribir, pero una excelente forma de aprender pruebas es estudiar teoremas relacionados y cómo se probaron.  4 Hacer preguntas. Está perfectamente bien quedar atrapado en una prueba. Pregúntele a su maestro o compañeros de clase si tiene preguntas. Pueden tener preguntas similares y pueden resolver los problemas juntos. Es mejor pedir aclaraciones que tropezar a ciegas con la prueba.
4 Hacer preguntas. Está perfectamente bien quedar atrapado en una prueba. Pregúntele a su maestro o compañeros de clase si tiene preguntas. Pueden tener preguntas similares y pueden resolver los problemas juntos. Es mejor pedir aclaraciones que tropezar a ciegas con la prueba.  1 Definir pruebas matemáticas. Una prueba matemática es una serie de enunciados lógicos soportados por teoremas y definiciones que prueban la verdad de otra afirmación matemática.[2] Las pruebas son la única forma de saber que una declaración es matemáticamente válida.
1 Definir pruebas matemáticas. Una prueba matemática es una serie de enunciados lógicos soportados por teoremas y definiciones que prueban la verdad de otra afirmación matemática.[2] Las pruebas son la única forma de saber que una declaración es matemáticamente válida.  2 Conoce a tu audiencia Antes de escribir una prueba, debe pensar en la audiencia para la que está escribiendo y qué información ya conocen. Si está escribiendo una prueba para su publicación, la escribirá de manera diferente a escribir una prueba para su clase de matemáticas de la escuela secundaria.[3]
2 Conoce a tu audiencia Antes de escribir una prueba, debe pensar en la audiencia para la que está escribiendo y qué información ya conocen. Si está escribiendo una prueba para su publicación, la escribirá de manera diferente a escribir una prueba para su clase de matemáticas de la escuela secundaria.[3]  3 Identifica el tipo de prueba que estás escribiendo. Existen diferentes tipos de pruebas y la que elijas depende de tu audiencia y de la tarea asignada. Si no está seguro de qué versión usar, pídale ayuda a su profesor. En la escuela secundaria, se puede esperar que escriba su prueba en un formato específico, como una prueba formal de dos columnas.[4]
3 Identifica el tipo de prueba que estás escribiendo. Existen diferentes tipos de pruebas y la que elijas depende de tu audiencia y de la tarea asignada. Si no está seguro de qué versión usar, pídale ayuda a su profesor. En la escuela secundaria, se puede esperar que escriba su prueba en un formato específico, como una prueba formal de dos columnas.[4]  4 Escriba la prueba de dos columnas como un bosquejo. La prueba de dos columnas es una manera fácil de organizar tus pensamientos y pensar en el problema. Dibuje una línea en el medio de la página y escriba todos los datos y declaraciones en el lado izquierdo. Escriba las definiciones / teoremas correspondientes en el lado derecho, junto a los datos que respaldan.
4 Escriba la prueba de dos columnas como un bosquejo. La prueba de dos columnas es una manera fácil de organizar tus pensamientos y pensar en el problema. Dibuje una línea en el medio de la página y escriba todos los datos y declaraciones en el lado izquierdo. Escriba las definiciones / teoremas correspondientes en el lado derecho, junto a los datos que respaldan.  5 Convierta la prueba de dos columnas a una prueba escrita informal. Utilizando la prueba de dos columnas como base, escriba la forma informal de párrafo de su prueba sin demasiados símbolos y abreviaturas.
5 Convierta la prueba de dos columnas a una prueba escrita informal. Utilizando la prueba de dos columnas como base, escriba la forma informal de párrafo de su prueba sin demasiados símbolos y abreviaturas.  1 Aprende el vocabulario de una prueba. Hay ciertas declaraciones y frases que verá una y otra vez en una prueba matemática. Estas son frases con las que debe familiarizarse y saber cómo usarlas correctamente al escribir su propia prueba.[6]
1 Aprende el vocabulario de una prueba. Hay ciertas declaraciones y frases que verá una y otra vez en una prueba matemática. Estas son frases con las que debe familiarizarse y saber cómo usarlas correctamente al escribir su propia prueba.[6] 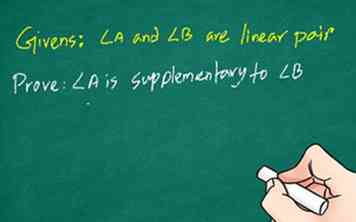 2 Escriba todos los datos. Al redactar una prueba, el primer paso es identificar y anotar todos los datos. Este es el mejor lugar para comenzar porque le ayuda a pensar qué se sabe y qué información necesitará para completar la prueba. Lee el problema y escribe cada uno.
2 Escriba todos los datos. Al redactar una prueba, el primer paso es identificar y anotar todos los datos. Este es el mejor lugar para comenzar porque le ayuda a pensar qué se sabe y qué información necesitará para completar la prueba. Lee el problema y escribe cada uno.  3 Definir todas las variables Además de escribir los datos, es útil definir todas las variables. Escriba las definiciones al comienzo de la prueba para evitar confusiones para el lector. Si las variables no están definidas, un lector puede perderse fácilmente al tratar de comprender su prueba.
3 Definir todas las variables Además de escribir los datos, es útil definir todas las variables. Escriba las definiciones al comienzo de la prueba para evitar confusiones para el lector. Si las variables no están definidas, un lector puede perderse fácilmente al tratar de comprender su prueba.  4 Trabaja con la prueba al revés. A menudo es más fácil pensar en el problema al revés. Comienza con la conclusión, lo que intentas probar, y piensa en los pasos que pueden llevarte al principio.[10]
4 Trabaja con la prueba al revés. A menudo es más fácil pensar en el problema al revés. Comienza con la conclusión, lo que intentas probar, y piensa en los pasos que pueden llevarte al principio.[10] 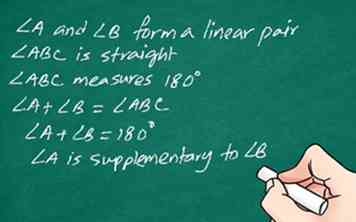 5 Ordene sus pasos lógicamente. Comience la prueba al principio y trabaje hacia la conclusión. Aunque es útil pensar en la prueba comenzando con la conclusión y trabajando hacia atrás, cuando realmente escribes la prueba, indica la conclusión al final.[11] Debe fluir de una declaración a otra, con soporte para cada declaración, de modo que no haya ninguna razón para dudar de la validez de su prueba.
5 Ordene sus pasos lógicamente. Comience la prueba al principio y trabaje hacia la conclusión. Aunque es útil pensar en la prueba comenzando con la conclusión y trabajando hacia atrás, cuando realmente escribes la prueba, indica la conclusión al final.[11] Debe fluir de una declaración a otra, con soporte para cada declaración, de modo que no haya ninguna razón para dudar de la validez de su prueba.  6 Evita usar flechas y abreviaturas en la prueba escrita. Cuando diseñe el plan para su prueba, puede usar taquigrafía y símbolos, pero al escribir la prueba final, símbolos como flechas pueden confundir al lector. En su lugar, use palabras como "luego" o "por lo tanto".[12]
6 Evita usar flechas y abreviaturas en la prueba escrita. Cuando diseñe el plan para su prueba, puede usar taquigrafía y símbolos, pero al escribir la prueba final, símbolos como flechas pueden confundir al lector. En su lugar, use palabras como "luego" o "por lo tanto".[12]  7 Admite todas las declaraciones con un teorema, ley o definición. Una prueba es solo tan buena como la evidencia utilizada. No puede hacer una afirmación sin apoyarla con una definición. Consulte otras pruebas similares a la que está trabajando, por ejemplo, evidencia.
7 Admite todas las declaraciones con un teorema, ley o definición. Una prueba es solo tan buena como la evidencia utilizada. No puede hacer una afirmación sin apoyarla con una definición. Consulte otras pruebas similares a la que está trabajando, por ejemplo, evidencia.  8 Termine con una conclusión o Q.E.D. La última declaración de la prueba debería ser el concepto que intentabas probar. Una vez que haya hecho esta afirmación, finalice la prueba con un símbolo de conclusión final como Q.E.D. o un cuadrado relleno indica que la prueba está completamente terminada.[14]
8 Termine con una conclusión o Q.E.D. La última declaración de la prueba debería ser el concepto que intentabas probar. Una vez que haya hecho esta afirmación, finalice la prueba con un símbolo de conclusión final como Q.E.D. o un cuadrado relleno indica que la prueba está completamente terminada.[14]