La intersección en y de una ecuación es un punto donde la gráfica de la ecuación se cruza con el eje Y. Hay varias maneras de encontrar la intersección en y de una ecuación, dependiendo de la información de inicio que tenga.
Método uno de tres:
Encontrar el Y-Intercept desde la pendiente y el punto
-
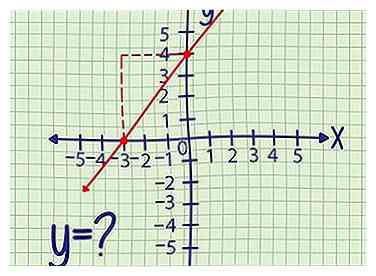 1 Escriba la pendiente y el punto. La pendiente o "subida sobre la carrera" es un número único que le indica qué tan empinada es la línea. Este tipo de problema también te da (x, y) coordenada de un punto a lo largo del gráfico. Pase a los otros métodos a continuación si no tiene estos dos datos.
1 Escriba la pendiente y el punto. La pendiente o "subida sobre la carrera" es un número único que le indica qué tan empinada es la línea. Este tipo de problema también te da (x, y) coordenada de un punto a lo largo del gráfico. Pase a los otros métodos a continuación si no tiene estos dos datos. - Ejemplo 1: Una línea recta con pendiente 2 contiene el punto (-3,4). Encuentre la intersección con el eje y de esta línea siguiendo los pasos a continuación.
-
 2 Aprende la forma pendiente-intersección de una ecuación. Cualquier línea recta se puede escribir como una ecuación en la forma y = mx + b. Cuando la ecuación está en esta forma, la variable metro es la pendiente, y segundo es el intercepto en y.
2 Aprende la forma pendiente-intersección de una ecuación. Cualquier línea recta se puede escribir como una ecuación en la forma y = mx + b. Cuando la ecuación está en esta forma, la variable metro es la pendiente, y segundo es el intercepto en y. -
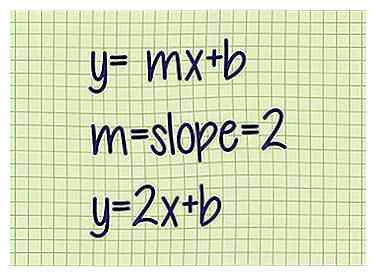 3 Sustituye la pendiente en esta ecuación. Escribe la ecuación pendiente-intersección, pero en lugar de metro, usa la pendiente de tu línea.
3 Sustituye la pendiente en esta ecuación. Escribe la ecuación pendiente-intersección, pero en lugar de metro, usa la pendiente de tu línea. - Ejemplo 1 (cont.): y = metrox + b
metro = pendiente = 2
y = 2x + b
- Ejemplo 1 (cont.): y = metrox + b
-
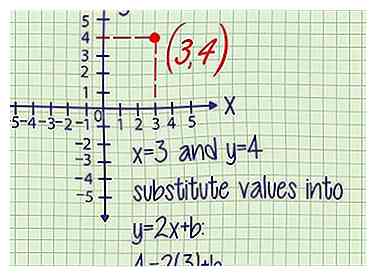 4 Reemplace xey con las coordenadas del punto. Cada vez que tenga las coordenadas de un solo punto en su línea, puede sustituirlas X y y coordenadas para el X y y en tu ecuación de línea Haz esto para la ecuación en la que has estado trabajando.
4 Reemplace xey con las coordenadas del punto. Cada vez que tenga las coordenadas de un solo punto en su línea, puede sustituirlas X y y coordenadas para el X y y en tu ecuación de línea Haz esto para la ecuación en la que has estado trabajando. - Ejemplo 1 (cont.): El punto (3,4) está en esta línea. En este punto, x = 3 y y = 4.
Sustituir estos valores en y = 2X + b:
4 = 2(3) + b
- Ejemplo 1 (cont.): El punto (3,4) está en esta línea. En este punto, x = 3 y y = 4.
-
 5 Resolver segundo. Recuerda, segundo es el intercepto en y de la línea. Ahora eso segundo es la única variable en la ecuación, reordenar para resolver esta variable y encontrar la respuesta.
5 Resolver segundo. Recuerda, segundo es el intercepto en y de la línea. Ahora eso segundo es la única variable en la ecuación, reordenar para resolver esta variable y encontrar la respuesta. - Ejemplo 1 (cont.): 4 = 2 (3) + b
4 = 6 + b
4 - 6 = b
-2 = b
El intercepto y de esta línea es -2.
- Ejemplo 1 (cont.): 4 = 2 (3) + b
-
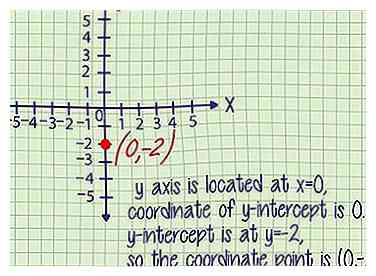 6 Escribe esto como un punto de coordenadas. La intersección con el eje y es el punto donde la línea se cruza con el eje y. Dado que el eje y se encuentra en x = 0, la coordenada x de la intersección en y es siempre 0.
6 Escribe esto como un punto de coordenadas. La intersección con el eje y es el punto donde la línea se cruza con el eje y. Dado que el eje y se encuentra en x = 0, la coordenada x de la intersección en y es siempre 0. - Ejemplo 1 (cont.): El intercepto y está en y = -2, por lo que el punto de coordenadas es (0, -2).
Método dos de tres:
Usando dos puntos
-
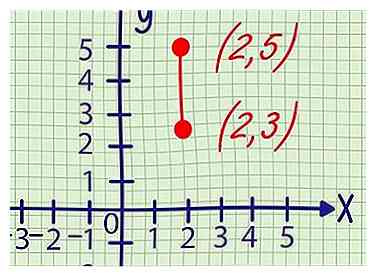 1 Escriba las coordenadas de ambos puntos. Este método cubre problemas que solo le indican dos puntos en una línea recta. Escribe cada coordenada de punto en forma (x, y).
1 Escriba las coordenadas de ambos puntos. Este método cubre problemas que solo le indican dos puntos en una línea recta. Escribe cada coordenada de punto en forma (x, y). -
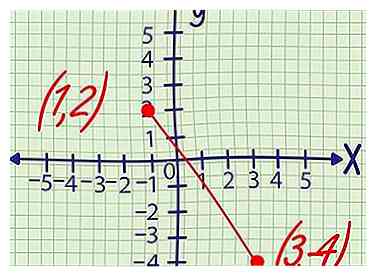 2 Ejemplo 2: Una línea recta pasa por puntos (1, 2) y (3, -4). Encuentre la intersección con el eje y de esta línea siguiendo los pasos a continuación.
2 Ejemplo 2: Una línea recta pasa por puntos (1, 2) y (3, -4). Encuentre la intersección con el eje y de esta línea siguiendo los pasos a continuación. -
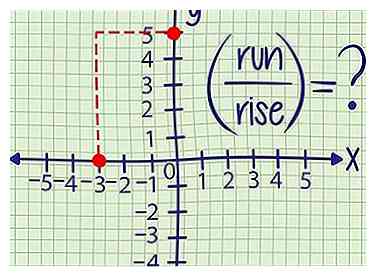 3 Calcule el ascenso y la carrera. La pendiente es una medida de la distancia vertical que la línea mueve para cada unidad de distancia horizontal. Es posible que haya escuchado esto descrito como "subir de carrera" () A continuación, le mostramos cómo encontrar estas dos cantidades a partir de dos puntos:
3 Calcule el ascenso y la carrera. La pendiente es una medida de la distancia vertical que la línea mueve para cada unidad de distancia horizontal. Es posible que haya escuchado esto descrito como "subir de carrera" () A continuación, le mostramos cómo encontrar estas dos cantidades a partir de dos puntos: - "Rise" es el cambio en la distancia vertical, o la diferencia entre el y-valores de los dos puntos.
- "Ejecutar" es el cambio en la distancia horizontal, o la diferencia entre X-valores de los mismos dos puntos.
- Ejemplo 2 (cont.): Los valores y de los dos puntos son 2 y -4, por lo que el aumento es (-4) - (2) = -6.
Los valores x de los dos puntos (en el mismo orden) son 1 y 3, por lo que la ejecución es 3 - 1 = 2.
-
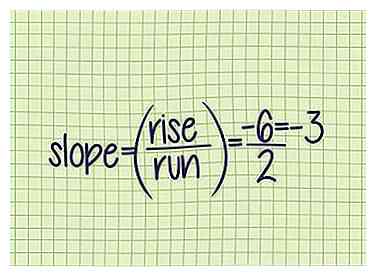 4 Divide subida por carrera para encontrar la pendiente. Ahora que conoce estos dos valores, conéctelos a ""para encontrar la pendiente de la línea.
4 Divide subida por carrera para encontrar la pendiente. Ahora que conoce estos dos valores, conéctelos a ""para encontrar la pendiente de la línea. - Ejemplo 2 (cont.): -3.
-
 5 Revise la forma pendiente-intersección. Puedes describir una línea recta con la fórmula y = mx + b, dónde metro es la pendiente y segundo es el intercepto en y. Ahora que sabemos la pendiente metro y un punto (x, y), podemos usar esta ecuación para resolver segundo, el intercepto y
5 Revise la forma pendiente-intersección. Puedes describir una línea recta con la fórmula y = mx + b, dónde metro es la pendiente y segundo es el intercepto en y. Ahora que sabemos la pendiente metro y un punto (x, y), podemos usar esta ecuación para resolver segundo, el intercepto y -
 6 Ajusta la pendiente y apunta a la ecuación. Tome la ecuación en forma pendiente-intersección y reemplace metro con la pendiente que calculó Reemplace la X y y términos con las coordenadas de un solo punto en la línea. No importa qué punto use.
6 Ajusta la pendiente y apunta a la ecuación. Tome la ecuación en forma pendiente-intersección y reemplace metro con la pendiente que calculó Reemplace la X y y términos con las coordenadas de un solo punto en la línea. No importa qué punto use. - Ejemplo 2 (cont.): y = mx + b
Pendiente = m = -3, entonces y = -3x + b
La línea incluye un punto con coordenadas (x, y) (1,2), por lo que 2 = -3 (1) + b.
- Ejemplo 2 (cont.): y = mx + b
-
 7 Resuelve para b. Ahora la única variable que queda en la ecuación es segundo, el intercepto y Reorganiza la ecuación para segundo está de un lado, y tú tienes tu respuesta. Recuerde, la intersección con el eje y siempre tiene una coordenada x de 0.
7 Resuelve para b. Ahora la única variable que queda en la ecuación es segundo, el intercepto y Reorganiza la ecuación para segundo está de un lado, y tú tienes tu respuesta. Recuerde, la intersección con el eje y siempre tiene una coordenada x de 0. - Ejemplo 2 (cont.): 2 = -3 (1) + b
2 = -3 + b
5 = b
La intersección con el eje y está en (0,5).
- Ejemplo 2 (cont.): 2 = -3 (1) + b
Método tres de tres:
Usando una ecuación
-
 1 Escriba la ecuación de la línea. Si ya tiene la ecuación de la línea, puede encontrar la intersección en y con un poco de álgebra.
1 Escriba la ecuación de la línea. Si ya tiene la ecuación de la línea, puede encontrar la intersección en y con un poco de álgebra. - Ejemplo 3: ¿Cuál es la intersección en y de la línea? x + 4y = 16?
- Nota: el ejemplo 3 es una línea recta. Consulte el final de esta sección para ver un ejemplo de una ecuación cuadrática (con una variable elevada a la potencia de 2).
-
 2 Sustituye 0 por x. El eje y es una línea vertical a lo largo de x = 0. Esto significa que cualquier punto en el eje y tiene una coordenada x de 0, incluida la intersección en y de la línea.Ingrese 0 para x en la ecuación de línea.
2 Sustituye 0 por x. El eje y es una línea vertical a lo largo de x = 0. Esto significa que cualquier punto en el eje y tiene una coordenada x de 0, incluida la intersección en y de la línea.Ingrese 0 para x en la ecuación de línea. - Ejemplo 3 (cont.): x + 4y = 16
x = 0
0 + 4y = 16
4y = 16
- Ejemplo 3 (cont.): x + 4y = 16
-
 3 Resuelve para y. La respuesta es el intercepto y de la línea.
3 Resuelve para y. La respuesta es el intercepto y de la línea. - Ejemplo 3 (cont.): 4y = 16
y = 4.
La intersección en y de la línea es 4.
- Ejemplo 3 (cont.): 4y = 16
-
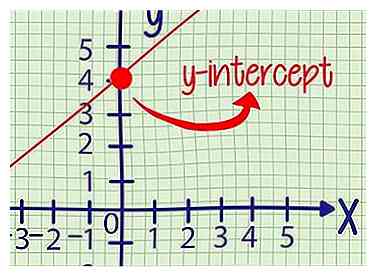 4 Confirmar mediante gráficos (opcional). Para verificar su respuesta, grafique la ecuación de la forma más clara posible. El punto donde la línea cruza el eje y es la intersección en y.
4 Confirmar mediante gráficos (opcional). Para verificar su respuesta, grafique la ecuación de la forma más clara posible. El punto donde la línea cruza el eje y es la intersección en y. -
 5 Encuentre la intersección en y para una ecuación cuadrática. Una ecuación cuadrática incluye una variable (x o y) elevada a la potencia de 2. Puedes resolver y con la misma sustitución, pero como la cuadrática describe una curva, podría interceptar el eje y en 0, 1 o 2 puntos. Esto significa que puede terminar con 0, 1 o 2 respuestas.
5 Encuentre la intersección en y para una ecuación cuadrática. Una ecuación cuadrática incluye una variable (x o y) elevada a la potencia de 2. Puedes resolver y con la misma sustitución, pero como la cuadrática describe una curva, podría interceptar el eje y en 0, 1 o 2 puntos. Esto significa que puede terminar con 0, 1 o 2 respuestas. - Ejemplo 4: Para encontrar la intersección en y de , sustituye x = 0 y resuelve la ecuación cuadrática.
En este caso, podemos resolver tomando la raíz cuadrada de ambos lados. Recuerde, al tomar una raíz cuadrada, debe dar cuenta de dos respuestas: una negativa y una positiva.
y = 1 o y = -1. Estas son intersecciones en y de esta curva.
- Ejemplo 4: Para encontrar la intersección en y de , sustituye x = 0 y resuelve la ecuación cuadrática.
 Minotauromaquia
Minotauromaquia
 1 Escriba la pendiente y el punto. La pendiente o "subida sobre la carrera" es un número único que le indica qué tan empinada es la línea. Este tipo de problema también te da (x, y) coordenada de un punto a lo largo del gráfico. Pase a los otros métodos a continuación si no tiene estos dos datos.
1 Escriba la pendiente y el punto. La pendiente o "subida sobre la carrera" es un número único que le indica qué tan empinada es la línea. Este tipo de problema también te da (x, y) coordenada de un punto a lo largo del gráfico. Pase a los otros métodos a continuación si no tiene estos dos datos.  2 Aprende la forma pendiente-intersección de una ecuación. Cualquier línea recta se puede escribir como una ecuación en la forma y = mx + b. Cuando la ecuación está en esta forma, la variable metro es la pendiente, y segundo es el intercepto en y.
2 Aprende la forma pendiente-intersección de una ecuación. Cualquier línea recta se puede escribir como una ecuación en la forma y = mx + b. Cuando la ecuación está en esta forma, la variable metro es la pendiente, y segundo es el intercepto en y. 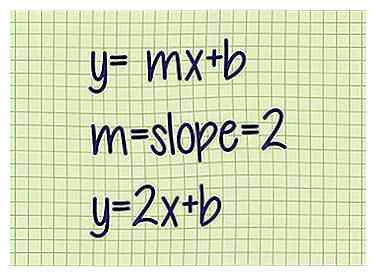 3 Sustituye la pendiente en esta ecuación. Escribe la ecuación pendiente-intersección, pero en lugar de metro, usa la pendiente de tu línea.
3 Sustituye la pendiente en esta ecuación. Escribe la ecuación pendiente-intersección, pero en lugar de metro, usa la pendiente de tu línea. 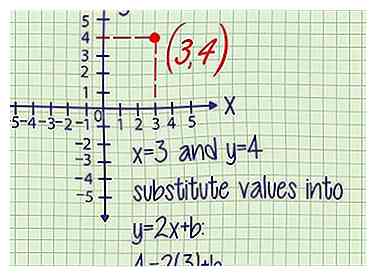 4 Reemplace xey con las coordenadas del punto. Cada vez que tenga las coordenadas de un solo punto en su línea, puede sustituirlas X y y coordenadas para el X y y en tu ecuación de línea Haz esto para la ecuación en la que has estado trabajando.
4 Reemplace xey con las coordenadas del punto. Cada vez que tenga las coordenadas de un solo punto en su línea, puede sustituirlas X y y coordenadas para el X y y en tu ecuación de línea Haz esto para la ecuación en la que has estado trabajando.  5 Resolver segundo. Recuerda, segundo es el intercepto en y de la línea. Ahora eso segundo es la única variable en la ecuación, reordenar para resolver esta variable y encontrar la respuesta.
5 Resolver segundo. Recuerda, segundo es el intercepto en y de la línea. Ahora eso segundo es la única variable en la ecuación, reordenar para resolver esta variable y encontrar la respuesta.  6 Escribe esto como un punto de coordenadas. La intersección con el eje y es el punto donde la línea se cruza con el eje y. Dado que el eje y se encuentra en x = 0, la coordenada x de la intersección en y es siempre 0.
6 Escribe esto como un punto de coordenadas. La intersección con el eje y es el punto donde la línea se cruza con el eje y. Dado que el eje y se encuentra en x = 0, la coordenada x de la intersección en y es siempre 0.  1 Escriba las coordenadas de ambos puntos. Este método cubre problemas que solo le indican dos puntos en una línea recta. Escribe cada coordenada de punto en forma (x, y).
1 Escriba las coordenadas de ambos puntos. Este método cubre problemas que solo le indican dos puntos en una línea recta. Escribe cada coordenada de punto en forma (x, y).  2 Ejemplo 2: Una línea recta pasa por puntos (1, 2) y (3, -4). Encuentre la intersección con el eje y de esta línea siguiendo los pasos a continuación.
2 Ejemplo 2: Una línea recta pasa por puntos (1, 2) y (3, -4). Encuentre la intersección con el eje y de esta línea siguiendo los pasos a continuación.  3 Calcule el ascenso y la carrera. La pendiente es una medida de la distancia vertical que la línea mueve para cada unidad de distancia horizontal. Es posible que haya escuchado esto descrito como "subir de carrera" (
3 Calcule el ascenso y la carrera. La pendiente es una medida de la distancia vertical que la línea mueve para cada unidad de distancia horizontal. Es posible que haya escuchado esto descrito como "subir de carrera" (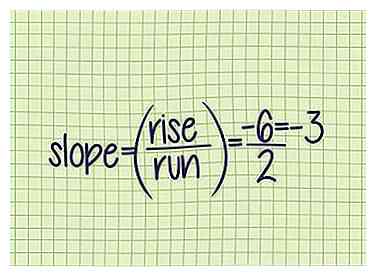 4 Divide subida por carrera para encontrar la pendiente. Ahora que conoce estos dos valores, conéctelos a "
4 Divide subida por carrera para encontrar la pendiente. Ahora que conoce estos dos valores, conéctelos a " 5 Revise la forma pendiente-intersección. Puedes describir una línea recta con la fórmula y = mx + b, dónde metro es la pendiente y segundo es el intercepto en y. Ahora que sabemos la pendiente metro y un punto (x, y), podemos usar esta ecuación para resolver segundo, el intercepto y
5 Revise la forma pendiente-intersección. Puedes describir una línea recta con la fórmula y = mx + b, dónde metro es la pendiente y segundo es el intercepto en y. Ahora que sabemos la pendiente metro y un punto (x, y), podemos usar esta ecuación para resolver segundo, el intercepto y  6 Ajusta la pendiente y apunta a la ecuación. Tome la ecuación en forma pendiente-intersección y reemplace metro con la pendiente que calculó Reemplace la X y y términos con las coordenadas de un solo punto en la línea. No importa qué punto use.
6 Ajusta la pendiente y apunta a la ecuación. Tome la ecuación en forma pendiente-intersección y reemplace metro con la pendiente que calculó Reemplace la X y y términos con las coordenadas de un solo punto en la línea. No importa qué punto use.  7 Resuelve para b. Ahora la única variable que queda en la ecuación es segundo, el intercepto y Reorganiza la ecuación para segundo está de un lado, y tú tienes tu respuesta. Recuerde, la intersección con el eje y siempre tiene una coordenada x de 0.
7 Resuelve para b. Ahora la única variable que queda en la ecuación es segundo, el intercepto y Reorganiza la ecuación para segundo está de un lado, y tú tienes tu respuesta. Recuerde, la intersección con el eje y siempre tiene una coordenada x de 0.  1 Escriba la ecuación de la línea. Si ya tiene la ecuación de la línea, puede encontrar la intersección en y con un poco de álgebra.
1 Escriba la ecuación de la línea. Si ya tiene la ecuación de la línea, puede encontrar la intersección en y con un poco de álgebra.  2 Sustituye 0 por x. El eje y es una línea vertical a lo largo de x = 0. Esto significa que cualquier punto en el eje y tiene una coordenada x de 0, incluida la intersección en y de la línea.Ingrese 0 para x en la ecuación de línea.
2 Sustituye 0 por x. El eje y es una línea vertical a lo largo de x = 0. Esto significa que cualquier punto en el eje y tiene una coordenada x de 0, incluida la intersección en y de la línea.Ingrese 0 para x en la ecuación de línea.  3 Resuelve para y. La respuesta es el intercepto y de la línea.
3 Resuelve para y. La respuesta es el intercepto y de la línea.  4 Confirmar mediante gráficos (opcional). Para verificar su respuesta, grafique la ecuación de la forma más clara posible. El punto donde la línea cruza el eje y es la intersección en y.
4 Confirmar mediante gráficos (opcional). Para verificar su respuesta, grafique la ecuación de la forma más clara posible. El punto donde la línea cruza el eje y es la intersección en y.  5 Encuentre la intersección en y para una ecuación cuadrática. Una ecuación cuadrática incluye una variable (x o y) elevada a la potencia de 2. Puedes resolver y con la misma sustitución, pero como la cuadrática describe una curva, podría interceptar el eje y en 0, 1 o 2 puntos. Esto significa que puede terminar con 0, 1 o 2 respuestas.
5 Encuentre la intersección en y para una ecuación cuadrática. Una ecuación cuadrática incluye una variable (x o y) elevada a la potencia de 2. Puedes resolver y con la misma sustitución, pero como la cuadrática describe una curva, podría interceptar el eje y en 0, 1 o 2 puntos. Esto significa que puede terminar con 0, 1 o 2 respuestas.