El factor de escala, o factor de escala lineal, es la relación de dos longitudes laterales correspondientes de figuras similares. Las figuras similares tienen la misma forma pero son de diferentes tamaños. El factor de escala se usa para resolver problemas geométricos básicos. Puede usar el factor de escala para encontrar las longitudes de los lados faltantes de una figura. Por el contrario, puede usar las longitudes laterales de dos figuras similares para calcular el factor de escala. Estos problemas implican la multiplicación o requieren que simplifique fracciones.
Método uno de cuatro:
Encontrar el factor de escala de figuras similares
-
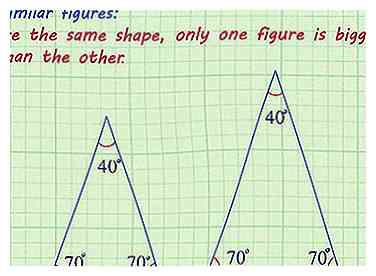 1 Verifica que las figuras sean similares. Figuras o formas similares, son aquellas en las que los ángulos son congruentes, y las longitudes laterales están en proporción. Las figuras similares tienen la misma forma, solo una figura es más grande que la otra.[1]
1 Verifica que las figuras sean similares. Figuras o formas similares, son aquellas en las que los ángulos son congruentes, y las longitudes laterales están en proporción. Las figuras similares tienen la misma forma, solo una figura es más grande que la otra.[1] - El problema debería indicarle que las formas son similares, o podría mostrarle que los ángulos son los mismos, y de otro modo indicar que las longitudes de los lados son proporcionales, a escala, o que se corresponden entre sí.
-
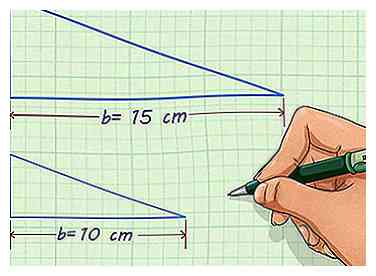 2 Encuentra la longitud de un lado correspondiente en cada figura. Es posible que deba girar o voltear la figura para que las dos formas se alineen y pueda identificar las longitudes de los lados correspondientes. Se le debe dar la longitud de estos dos lados, o debería poder medirlos.[2] Si no conoce al menos una longitud lateral de cada figura, no puede encontrar el factor de escala.
2 Encuentra la longitud de un lado correspondiente en cada figura. Es posible que deba girar o voltear la figura para que las dos formas se alineen y pueda identificar las longitudes de los lados correspondientes. Se le debe dar la longitud de estos dos lados, o debería poder medirlos.[2] Si no conoce al menos una longitud lateral de cada figura, no puede encontrar el factor de escala. - Por ejemplo, puede tener un triángulo con una base de 15 cm de largo y un triángulo similar con una base de 10 cm de largo.
-
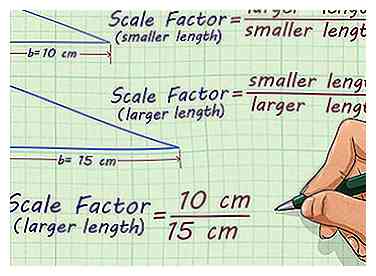 3 Configura una proporción. Para cada par de figuras similares, hay dos factores de escala: uno que usa al escalar y otro que usa al escalar. Si está escalando de una figura más pequeña a una más grande, use la relación . Si está reduciendo de una figura más grande a una más pequeña, use la proporción .[3]
3 Configura una proporción. Para cada par de figuras similares, hay dos factores de escala: uno que usa al escalar y otro que usa al escalar. Si está escalando de una figura más pequeña a una más grande, use la relación . Si está reduciendo de una figura más grande a una más pequeña, use la proporción .[3] - Por ejemplo, si está reduciendo de un triángulo con una base de 15 cm a uno con una base de 10 cm, usaría la relación .
Llenando los valores apropiados, se convierte en .
- Por ejemplo, si está reduciendo de un triángulo con una base de 15 cm a uno con una base de 10 cm, usaría la relación .
-
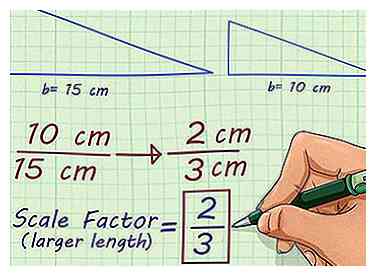 4 Simplifica la proporción. La proporción simplificada, o fracción, le dará su factor de escala. Si está reduciendo la escala, su factor de escala será una fracción adecuada.[4] Si está escalando, será un número entero o fracción impropia, que puede convertir a decimal.
4 Simplifica la proporción. La proporción simplificada, o fracción, le dará su factor de escala. Si está reduciendo la escala, su factor de escala será una fracción adecuada.[4] Si está escalando, será un número entero o fracción impropia, que puede convertir a decimal. - Por ejemplo, la relación simplifica a . Entonces, el factor de escala de dos triángulos, uno con una base de 15 cm y otro con una base de 10 cm, es .
Método dos de cuatro:
Encontrar una figura similar usando el factor de escala
-
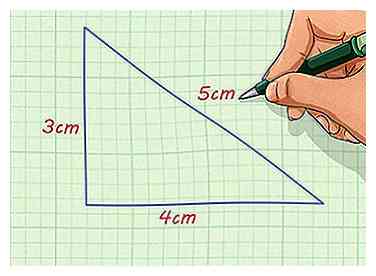 1 Encuentra las longitudes laterales de la figura. Debería tener una figura de la que las longitudes de los lados son dadas o medibles. Si no puede determinar las longitudes laterales de la figura, no puede hacer una figura similar.
1 Encuentra las longitudes laterales de la figura. Debería tener una figura de la que las longitudes de los lados son dadas o medibles. Si no puede determinar las longitudes laterales de la figura, no puede hacer una figura similar. - Por ejemplo, puede tener un triángulo rectángulo con lados de 4 cm y 3 cm y una hipotenusa de 5 cm de largo.
-
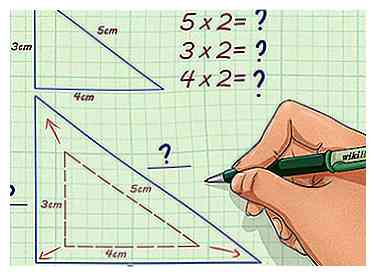 2 Determine si está escalando hacia arriba o hacia abajo. Si está escalando, su figura faltante será más grande, y el factor de escala será un número entero, fracción impropia o decimal. Si está reduciendo la escala, su figura faltante será más pequeña, y su factor de escala probablemente será una fracción adecuada.
2 Determine si está escalando hacia arriba o hacia abajo. Si está escalando, su figura faltante será más grande, y el factor de escala será un número entero, fracción impropia o decimal. Si está reduciendo la escala, su figura faltante será más pequeña, y su factor de escala probablemente será una fracción adecuada. - Por ejemplo, si el factor de escala es 2, entonces está escalando, y la cifra similar será mayor que la que tiene.
-
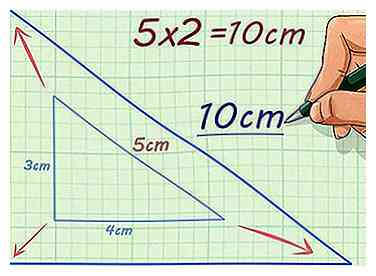 3 Multiplique una longitud lateral por el factor de escala. El factor de escala se le debe dar a usted. Cuando multiplicas la longitud del lado por el factor de escala, esto te da la longitud del lado correspondiente faltante en la figura similar.[5]
3 Multiplique una longitud lateral por el factor de escala. El factor de escala se le debe dar a usted. Cuando multiplicas la longitud del lado por el factor de escala, esto te da la longitud del lado correspondiente faltante en la figura similar.[5] - Por ejemplo, si la hipotenusa de un triángulo rectángulo es de 5 cm de largo, y el factor de escala es 2, para encontrar la hipotenusa del triángulo similar, se calcularía . Entonces el triángulo similar tiene una hipotenusa de 10 cm de largo.
-
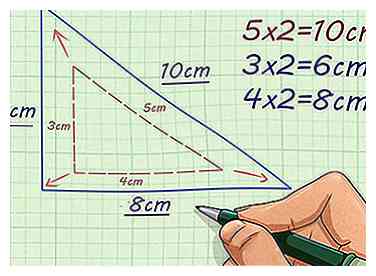 4 Encuentra las longitudes laterales restantes de la figura. Continúa multiplicando la longitud de cada lado por el factor de escala. Esto le dará las longitudes laterales correspondientes de la figura faltante.
4 Encuentra las longitudes laterales restantes de la figura. Continúa multiplicando la longitud de cada lado por el factor de escala. Esto le dará las longitudes laterales correspondientes de la figura faltante. - Por ejemplo, si la base de un triángulo rectángulo es de 3 cm de largo, con un factor de escala de 2, se calcularía para encontrar la base del triángulo similar. Si la altura de un triángulo rectángulo es de 4 cm de largo, con un factor de escala de 2 se calcularía para encontrar la altura del triángulo similar.
Método tres de cuatro:
Completando problemas de muestra
-
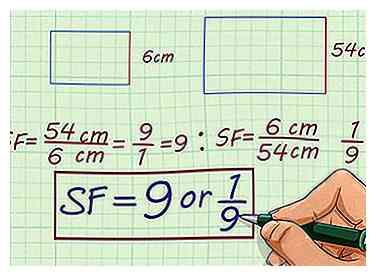 1 Encuentre el factor de escala de estas figuras similares: un rectángulo con una altura de 6 cm y un rectángulo con una altura de 54 cm.
1 Encuentre el factor de escala de estas figuras similares: un rectángulo con una altura de 6 cm y un rectángulo con una altura de 54 cm. - Crea una relación que compare las dos alturas. Ampliando, la relación es . Escalando hacia abajo, la relación es .
- Simplifica la proporción. El radio simplifica a . El radio simplifica a . Entonces, los dos rectángulos tienen un factor de escala de o .
-
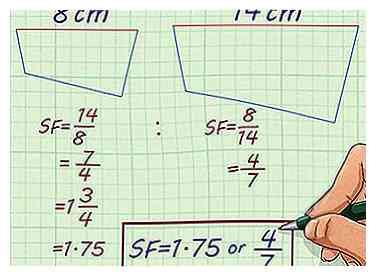 2 Prueba este problema Un polígono irregular tiene 14 cm de largo en su punto más ancho. Un polígono irregular similar es de 8 pulgadas en su punto más ancho. ¿Cuál es el factor de escala?
2 Prueba este problema Un polígono irregular tiene 14 cm de largo en su punto más ancho. Un polígono irregular similar es de 8 pulgadas en su punto más ancho. ¿Cuál es el factor de escala? - Las figuras irregulares pueden ser similares si todos sus lados están en proporción. Por lo tanto, puedes calcular un factor de escala usando cualquier dimensión que se te dé.[6]
- Como conoce el ancho de cada polígono, puede establecer una proporción comparándolos. Ampliando, la relación es . Escalando hacia abajo, la relación es .
- Simplifica la proporción. El radio simplifica a . El radio simplifica a . Entonces, los dos polígonos irregulares tienen un factor de escala de o .
-
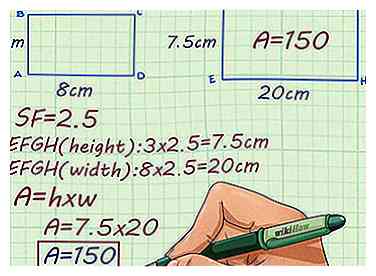 3 Use el factor de escala para responder este problema. Rectángulo ABCD mide 8cm x 3cm. Rectángulo EFGH es un rectángulo más grande y similar. Usando un factor de escala de 2.5, ¿cuál es el área de Rectángulo EFGH?
3 Use el factor de escala para responder este problema. Rectángulo ABCD mide 8cm x 3cm. Rectángulo EFGH es un rectángulo más grande y similar. Usando un factor de escala de 2.5, ¿cuál es el área de Rectángulo EFGH? - Multiplique la altura de Rectángulo ABCD por el factor de escala. Esto le dará la altura de Rectángulo EFGH: .
- Multiplique el ancho de Rectángulo ABCD por el factor de escala. Esto le dará el ancho de Rectángulo EFGH: .
- Multiplique la altura y el ancho de Rectángulo EFGH para encontrar el área: . Entonces, el área de Rectangle EFGH es de 150 centímetros cuadrados.
Método cuatro de cuatro:
Encontrar el factor de escala en química
-
 1 Divida la masa molar del compuesto por la de la fórmula empírica. Cuando se tiene la fórmula empírica de un compuesto químico y se necesita encontrar la fórmula molecular de ese mismo compuesto químico, se puede encontrar el factor de escala que se necesita dividiendo la masa molar del compuesto por la masa molar de la fórmula empírica.
1 Divida la masa molar del compuesto por la de la fórmula empírica. Cuando se tiene la fórmula empírica de un compuesto químico y se necesita encontrar la fórmula molecular de ese mismo compuesto químico, se puede encontrar el factor de escala que se necesita dividiendo la masa molar del compuesto por la masa molar de la fórmula empírica. - Por ejemplo, puede que necesite encontrar la masa molar de un compuesto H2O con una masa molar de 54.05 g / mol.
- La masa molar de H2O es 18.0152 g / mol.
- Encuentre el factor de escala dividiendo la masa molar del compuesto por la masa molar de la fórmula empírica:
- Factor de escala = 54.05 / 18.0152 = 3
- Por ejemplo, puede que necesite encontrar la masa molar de un compuesto H2O con una masa molar de 54.05 g / mol.
-
 2 Multiplica la fórmula empírica por el factor de escala. Multiplique los subíndices de cada elemento dentro de la fórmula empírica por el factor de escala que acaba de calcular. Esto le dará la fórmula molecular de la muestra del compuesto químico involucrado en el problema.
2 Multiplica la fórmula empírica por el factor de escala. Multiplique los subíndices de cada elemento dentro de la fórmula empírica por el factor de escala que acaba de calcular. Esto le dará la fórmula molecular de la muestra del compuesto químico involucrado en el problema. - Por ejemplo, para encontrar la fórmula molecular del compuesto en cuestión, multiplique los subíndices de H20 por el factor de escala de 3.
- H2O * 3 = H6O3
- Por ejemplo, para encontrar la fórmula molecular del compuesto en cuestión, multiplique los subíndices de H20 por el factor de escala de 3.
-
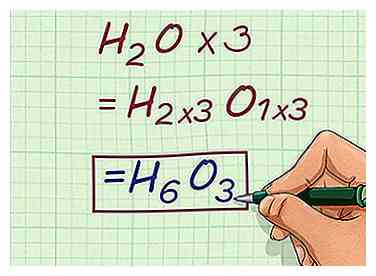 3 Escribe la respuesta. Con esta respuesta, ha encontrado con éxito la respuesta para la fórmula empírica, así como la fórmula molecular del compuesto químico involucrado en el problema.
3 Escribe la respuesta. Con esta respuesta, ha encontrado con éxito la respuesta para la fórmula empírica, así como la fórmula molecular del compuesto químico involucrado en el problema. - Por ejemplo, el factor de escala para el compuesto es 3. La fórmula molecular del compuesto es H6O3.
 Minotauromaquia
Minotauromaquia
 1 Verifica que las figuras sean similares. Figuras o formas similares, son aquellas en las que los ángulos son congruentes, y las longitudes laterales están en proporción. Las figuras similares tienen la misma forma, solo una figura es más grande que la otra.[1]
1 Verifica que las figuras sean similares. Figuras o formas similares, son aquellas en las que los ángulos son congruentes, y las longitudes laterales están en proporción. Las figuras similares tienen la misma forma, solo una figura es más grande que la otra.[1]  2 Encuentra la longitud de un lado correspondiente en cada figura. Es posible que deba girar o voltear la figura para que las dos formas se alineen y pueda identificar las longitudes de los lados correspondientes. Se le debe dar la longitud de estos dos lados, o debería poder medirlos.[2] Si no conoce al menos una longitud lateral de cada figura, no puede encontrar el factor de escala.
2 Encuentra la longitud de un lado correspondiente en cada figura. Es posible que deba girar o voltear la figura para que las dos formas se alineen y pueda identificar las longitudes de los lados correspondientes. Se le debe dar la longitud de estos dos lados, o debería poder medirlos.[2] Si no conoce al menos una longitud lateral de cada figura, no puede encontrar el factor de escala.  3 Configura una proporción. Para cada par de figuras similares, hay dos factores de escala: uno que usa al escalar y otro que usa al escalar. Si está escalando de una figura más pequeña a una más grande, use la relación
3 Configura una proporción. Para cada par de figuras similares, hay dos factores de escala: uno que usa al escalar y otro que usa al escalar. Si está escalando de una figura más pequeña a una más grande, use la relación  4 Simplifica la proporción. La proporción simplificada, o fracción, le dará su factor de escala. Si está reduciendo la escala, su factor de escala será una fracción adecuada.[4] Si está escalando, será un número entero o fracción impropia, que puede convertir a decimal.
4 Simplifica la proporción. La proporción simplificada, o fracción, le dará su factor de escala. Si está reduciendo la escala, su factor de escala será una fracción adecuada.[4] Si está escalando, será un número entero o fracción impropia, que puede convertir a decimal.  1 Encuentra las longitudes laterales de la figura. Debería tener una figura de la que las longitudes de los lados son dadas o medibles. Si no puede determinar las longitudes laterales de la figura, no puede hacer una figura similar.
1 Encuentra las longitudes laterales de la figura. Debería tener una figura de la que las longitudes de los lados son dadas o medibles. Si no puede determinar las longitudes laterales de la figura, no puede hacer una figura similar.  2 Determine si está escalando hacia arriba o hacia abajo. Si está escalando, su figura faltante será más grande, y el factor de escala será un número entero, fracción impropia o decimal. Si está reduciendo la escala, su figura faltante será más pequeña, y su factor de escala probablemente será una fracción adecuada.
2 Determine si está escalando hacia arriba o hacia abajo. Si está escalando, su figura faltante será más grande, y el factor de escala será un número entero, fracción impropia o decimal. Si está reduciendo la escala, su figura faltante será más pequeña, y su factor de escala probablemente será una fracción adecuada.  3 Multiplique una longitud lateral por el factor de escala. El factor de escala se le debe dar a usted. Cuando multiplicas la longitud del lado por el factor de escala, esto te da la longitud del lado correspondiente faltante en la figura similar.[5]
3 Multiplique una longitud lateral por el factor de escala. El factor de escala se le debe dar a usted. Cuando multiplicas la longitud del lado por el factor de escala, esto te da la longitud del lado correspondiente faltante en la figura similar.[5]  4 Encuentra las longitudes laterales restantes de la figura. Continúa multiplicando la longitud de cada lado por el factor de escala. Esto le dará las longitudes laterales correspondientes de la figura faltante.
4 Encuentra las longitudes laterales restantes de la figura. Continúa multiplicando la longitud de cada lado por el factor de escala. Esto le dará las longitudes laterales correspondientes de la figura faltante.  1 Encuentre el factor de escala de estas figuras similares: un rectángulo con una altura de 6 cm y un rectángulo con una altura de 54 cm.
1 Encuentre el factor de escala de estas figuras similares: un rectángulo con una altura de 6 cm y un rectángulo con una altura de 54 cm.  2 Prueba este problema Un polígono irregular tiene 14 cm de largo en su punto más ancho. Un polígono irregular similar es de 8 pulgadas en su punto más ancho. ¿Cuál es el factor de escala?
2 Prueba este problema Un polígono irregular tiene 14 cm de largo en su punto más ancho. Un polígono irregular similar es de 8 pulgadas en su punto más ancho. ¿Cuál es el factor de escala?  3 Use el factor de escala para responder este problema. Rectángulo ABCD mide 8cm x 3cm. Rectángulo EFGH es un rectángulo más grande y similar. Usando un factor de escala de 2.5, ¿cuál es el área de Rectángulo EFGH?
3 Use el factor de escala para responder este problema. Rectángulo ABCD mide 8cm x 3cm. Rectángulo EFGH es un rectángulo más grande y similar. Usando un factor de escala de 2.5, ¿cuál es el área de Rectángulo EFGH?  1 Divida la masa molar del compuesto por la de la fórmula empírica. Cuando se tiene la fórmula empírica de un compuesto químico y se necesita encontrar la fórmula molecular de ese mismo compuesto químico, se puede encontrar el factor de escala que se necesita dividiendo la masa molar del compuesto por la masa molar de la fórmula empírica.
1 Divida la masa molar del compuesto por la de la fórmula empírica. Cuando se tiene la fórmula empírica de un compuesto químico y se necesita encontrar la fórmula molecular de ese mismo compuesto químico, se puede encontrar el factor de escala que se necesita dividiendo la masa molar del compuesto por la masa molar de la fórmula empírica.  2 Multiplica la fórmula empírica por el factor de escala. Multiplique los subíndices de cada elemento dentro de la fórmula empírica por el factor de escala que acaba de calcular. Esto le dará la fórmula molecular de la muestra del compuesto químico involucrado en el problema.
2 Multiplica la fórmula empírica por el factor de escala. Multiplique los subíndices de cada elemento dentro de la fórmula empírica por el factor de escala que acaba de calcular. Esto le dará la fórmula molecular de la muestra del compuesto químico involucrado en el problema. 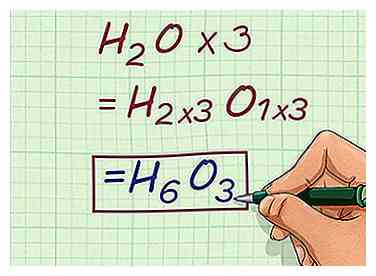 3 Escribe la respuesta. Con esta respuesta, ha encontrado con éxito la respuesta para la fórmula empírica, así como la fórmula molecular del compuesto químico involucrado en el problema.
3 Escribe la respuesta. Con esta respuesta, ha encontrado con éxito la respuesta para la fórmula empírica, así como la fórmula molecular del compuesto químico involucrado en el problema.