Un múltiplo es el resultado de multiplicar un número por un número entero. El mínimo común múltiplo (LCM) de un grupo de números es el número más pequeño que es un múltiplo de todos los números. Para encontrar el mínimo común múltiplo, debe ser capaz de identificar los factores de los números con los que está trabajando. Puede usar algunos métodos diferentes para encontrar el múltiplo menos común. Estos métodos también funcionan cuando se encuentra el LCM de más de dos números.
Método uno de cuatro:
Listado de todos los múltiplos
-
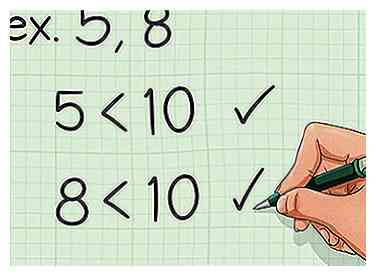 1 Evalúa tus números Este método funciona mejor cuando trabaja con dos números que son menos de 10. Si trabaja con números más grandes, lo mejor es usar un método diferente.
1 Evalúa tus números Este método funciona mejor cuando trabaja con dos números que son menos de 10. Si trabaja con números más grandes, lo mejor es usar un método diferente. - Por ejemplo, es posible que necesite encontrar el mínimo común múltiplo de 5 y 8. Dado que estos son números pequeños, es apropiado utilizar este método.
-
 2 Escriba los primeros varios múltiplos del primer número. Un múltiplo es un producto de cualquier número y entero.[1] En otras palabras, son los números que verías en una tabla de multiplicar.
2 Escriba los primeros varios múltiplos del primer número. Un múltiplo es un producto de cualquier número y entero.[1] En otras palabras, son los números que verías en una tabla de multiplicar. - Por ejemplo, los primeros múltiplos de 5 son 5, 10, 15, 20, 25, 30, 35 y 40.
-
 3 Escriba los primeros varios múltiplos del segundo número. Haga esto cerca del primer conjunto de múltiplos, para que sean fáciles de comparar.
3 Escriba los primeros varios múltiplos del segundo número. Haga esto cerca del primer conjunto de múltiplos, para que sean fáciles de comparar. - Por ejemplo, los primeros múltiplos de 8 son 8, 16, 24, 32, 40, 48, 56 y 64.
-
 4 Encuentra el múltiplo más pequeño que los números tienen en común. Es posible que deba extender su lista de múltiplos hasta que encuentre una que ambos comparten. Este número será su múltiplo menos común.[2]
4 Encuentra el múltiplo más pequeño que los números tienen en común. Es posible que deba extender su lista de múltiplos hasta que encuentre una que ambos comparten. Este número será su múltiplo menos común.[2] - Por ejemplo, el múltiplo más bajo 5 y 8 comparten 40, por lo que el múltiplo menos común de 5 y 8 es 40.
Método dos de cuatro:
Usando factorización prima
-
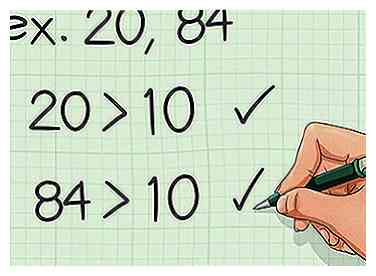 1 Evalúa tus números Este método funciona mejor cuando los números con los que está trabajando son mayores que 10. Si tiene números más pequeños, puede usar un método diferente para encontrar el múltiplo menos común más rápidamente.
1 Evalúa tus números Este método funciona mejor cuando los números con los que está trabajando son mayores que 10. Si tiene números más pequeños, puede usar un método diferente para encontrar el múltiplo menos común más rápidamente. - Por ejemplo, si necesita encontrar el mínimo común múltiplo de 20 y 84, debe usar este método.
-
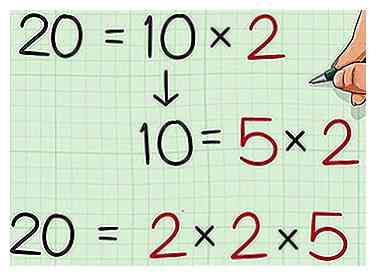 2 Factoriza el primer número. Desea factorizar el número en sus factores primos; es decir, encuentre los factores principales que puede multiplicar para obtener este número. Una forma de hacerlo es creando un árbol de factores. Una vez que haya terminado de factorizar, vuelva a escribir los factores primos como una ecuación.
2 Factoriza el primer número. Desea factorizar el número en sus factores primos; es decir, encuentre los factores principales que puede multiplicar para obtener este número. Una forma de hacerlo es creando un árbol de factores. Una vez que haya terminado de factorizar, vuelva a escribir los factores primos como una ecuación. - Por ejemplo, y , entonces los factores primos de 20 son 2, 2 y 5. Reescribiendo como una ecuación, obtienes .
-
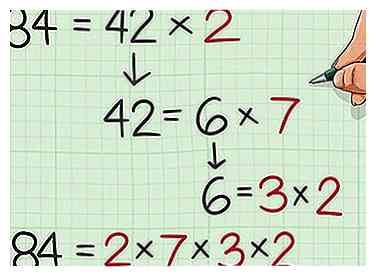 3 Factoriza el segundo número. Haga esto de la misma manera que factorizó el primer número, encontrando los factores primos que puede multiplicar juntos para obtener el número.
3 Factoriza el segundo número. Haga esto de la misma manera que factorizó el primer número, encontrando los factores primos que puede multiplicar juntos para obtener el número. - Por ejemplo, , y , entonces los factores primos de 84 son 2, 7, 3 y 2. Reescribiendo como una ecuación, obtienes .
-
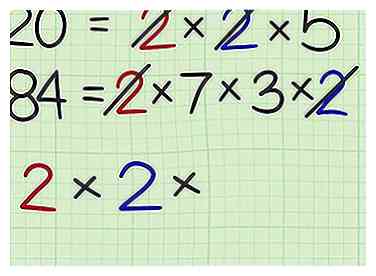 4 Escriba los factores que cada número comparte. Escribe los factores como una oración de multiplicación. A medida que escribe cada factor, sepárelo en cada ecuación de factorización de los números.
4 Escriba los factores que cada número comparte. Escribe los factores como una oración de multiplicación. A medida que escribe cada factor, sepárelo en cada ecuación de factorización de los números. - Por ejemplo, ambos números comparten un factor de 2, así que escriba y tache un 2 en la ecuación de factorización de cada número.
- Cada número también comparte un segundo 2, así que cambie la oración de multiplicación a y tachar un segundo 2 en cada ecuación de factorización.
-
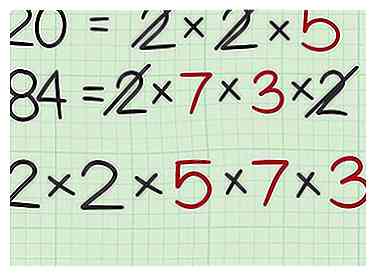 5 Agregue los factores sobrantes a la oración de multiplicación. Estos son los factores que no tachó cuando comparó los dos grupos de factores. Por lo tanto, estos son factores que los dos números no comparten.[3]
5 Agregue los factores sobrantes a la oración de multiplicación. Estos son los factores que no tachó cuando comparó los dos grupos de factores. Por lo tanto, estos son factores que los dos números no comparten.[3] - Por ejemplo, en la ecuación , tachó ambos 2, ya que estos factores se compartieron con el otro número. Te queda un factor de 5, así que agrega esto a tu oración de multiplicación: .
- En la ecuación , también tachaste los 2s. Usted tiene los factores 7 y 3 sobrantes, así que agréguelos a su oración de multiplicación: .
-
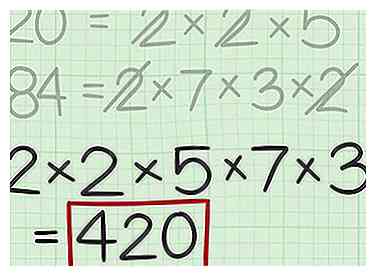 6 Calcula el mínimo común múltiplo. Para hacer esto, multiplica todos los factores en tu oración de multiplicación.
6 Calcula el mínimo común múltiplo. Para hacer esto, multiplica todos los factores en tu oración de multiplicación. - Por ejemplo, . Entonces, el mínimo común múltiplo de 20 y 84 es 420.
Método tres de cuatro:
Usando el método de cuadrícula o escalera
-
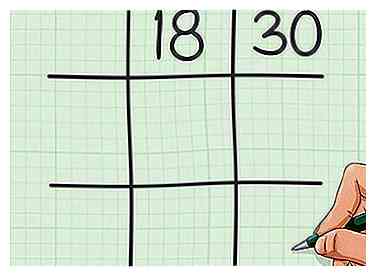 1 Dibuja una cuadrícula de tres en raya. Una cuadrícula tic-tac-toe es dos conjuntos de líneas paralelas que se intersectan perpendicularmente. Las líneas forman tres filas y tres columnas y se parecen a la tecla numeral (#) en un teléfono o teclado. Escribe tu primer número en el cuadrado superior central de la grilla. Escribe tu segundo número en el recuadro superior derecho de la grilla.[4]
1 Dibuja una cuadrícula de tres en raya. Una cuadrícula tic-tac-toe es dos conjuntos de líneas paralelas que se intersectan perpendicularmente. Las líneas forman tres filas y tres columnas y se parecen a la tecla numeral (#) en un teléfono o teclado. Escribe tu primer número en el cuadrado superior central de la grilla. Escribe tu segundo número en el recuadro superior derecho de la grilla.[4] - Por ejemplo, si está tratando de encontrar el mínimo común múltiplo de 18 y 30, escriba 18 en la parte superior central de su cuadrícula y 30 en la parte superior derecha de su cuadrícula.
-
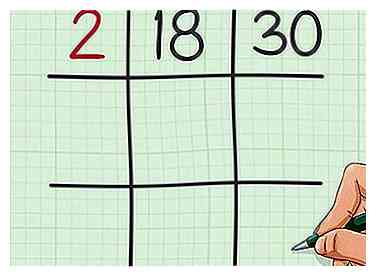 2 Busque un factor que sea común a ambos números. Escribe este número en el cuadrado superior izquierdo de tu grilla. Es útil usar factores primos, pero no necesariamente es necesario.
2 Busque un factor que sea común a ambos números. Escribe este número en el cuadrado superior izquierdo de tu grilla. Es útil usar factores primos, pero no necesariamente es necesario. - Por ejemplo, dado que 18 y 30 son números pares, usted sabe que ambos tienen un factor de 2.Entonces escribe 2 en la esquina superior izquierda de la grilla.
-
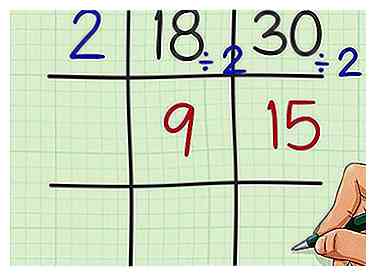 3 Divide el factor en cada número. Escribe el cociente en el cuadrado debajo de cualquier número. Un cociente es la respuesta a un problema de división.
3 Divide el factor en cada número. Escribe el cociente en el cuadrado debajo de cualquier número. Un cociente es la respuesta a un problema de división. - Por ejemplo, , entonces escribe 9 bajo 18 en la grilla.
- , entonces escribe 15 debajo de 30 en la grilla.
-
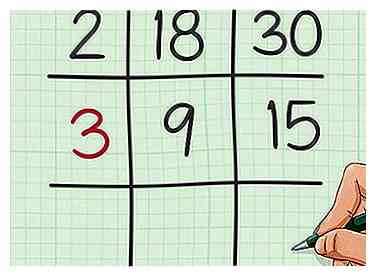 4 Encuentre un factor que sea común a los dos cocientes. Si no hay un factor común para ambos cocientes, puede omitir este y el siguiente paso. Si hay un factor común, escríbalo en el recuadro de la mitad izquierda de la cuadrícula.
4 Encuentre un factor que sea común a los dos cocientes. Si no hay un factor común para ambos cocientes, puede omitir este y el siguiente paso. Si hay un factor común, escríbalo en el recuadro de la mitad izquierda de la cuadrícula. - Por ejemplo, 9 y 15 tienen un factor de 3, por lo que escribiría 3 en la mitad izquierda de la cuadrícula.
-
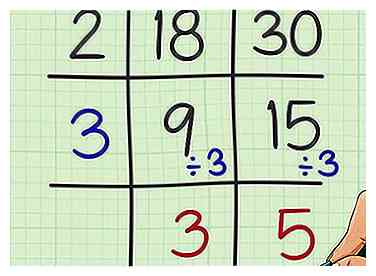 5 Divida este nuevo factor en cada cociente. Escribe este nuevo cociente debajo de los primeros.
5 Divida este nuevo factor en cada cociente. Escribe este nuevo cociente debajo de los primeros. - Por ejemplo, , entonces escribe 3 en 9 en la grilla.
- , entonces escribe 5 debajo de 15 en la grilla.
-
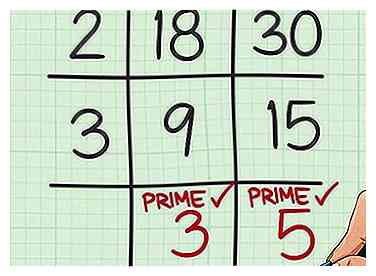 6 Extiende tu grilla si es necesario. Siga este mismo proceso hasta llegar a un punto donde el último conjunto de cocientes no tenga un factor en común.
6 Extiende tu grilla si es necesario. Siga este mismo proceso hasta llegar a un punto donde el último conjunto de cocientes no tenga un factor en común. -
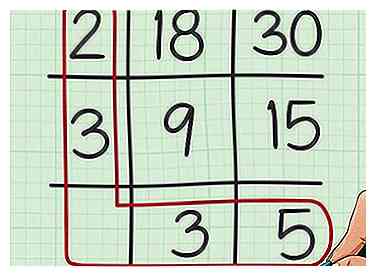 7 Dibuja un círculo alrededor de los números en la primera columna y la última fila de tu grilla. Puedes pensar que está dibujando una "L" para "múltiplo mínimo común". Escribe una oración de multiplicación usando todos estos factores.[5]
7 Dibuja un círculo alrededor de los números en la primera columna y la última fila de tu grilla. Puedes pensar que está dibujando una "L" para "múltiplo mínimo común". Escribe una oración de multiplicación usando todos estos factores.[5] - Por ejemplo, dado que 2 y 3 están en la primera columna de la grilla, y 3 y 5 están en la última fila de la grilla, usted escribiría la oración .
-
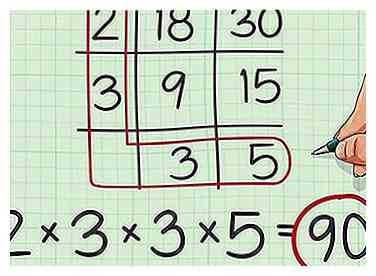 8 Completa la multiplicación. Cuando multiplicas todos estos factores juntos, el resultado es el múltiplo menos común de tus dos números originales.[6]
8 Completa la multiplicación. Cuando multiplicas todos estos factores juntos, el resultado es el múltiplo menos común de tus dos números originales.[6] - Por ejemplo, . Entonces, el mínimo común múltiplo de 18 y 30 es 90.
Método cuatro de cuatro:
Usando el algoritmo de Euclides
-
 1 Comprende el vocabulario de la división. El dividendo es el número que se divide. El divisor es el número por el que se divide el dividendo. El cociente es la respuesta al problema de la división. El resto es la cantidad que queda después de que un número se divide por otro.[7]
1 Comprende el vocabulario de la división. El dividendo es el número que se divide. El divisor es el número por el que se divide el dividendo. El cociente es la respuesta al problema de la división. El resto es la cantidad que queda después de que un número se divide por otro.[7] - Por ejemplo, en la ecuación :
15 es el dividendo
6 es el divisor
2 es el cociente
3 es el resto.
- Por ejemplo, en la ecuación :
-
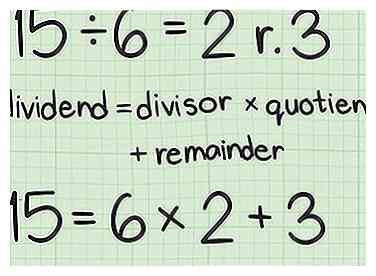 2 Configure la fórmula para el formulario cociente-resto. La fórmula es .[8] Utilizará este formulario para configurar el algoritmo de Euclid para encontrar el mayor divisor común de dos números.
2 Configure la fórmula para el formulario cociente-resto. La fórmula es .[8] Utilizará este formulario para configurar el algoritmo de Euclid para encontrar el mayor divisor común de dos números. - Por ejemplo, .
- El mayor divisor común es el divisor más grande, o factor, que comparten dos números.[9]
- En este método, primero encontrará el divisor común más grande y luego lo usará para encontrar el mínimo común múltiplo.
-
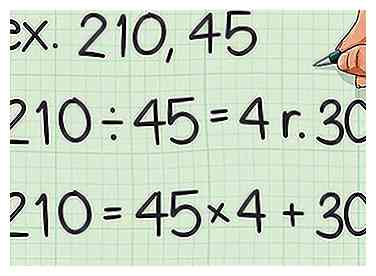 3 Usa el mayor de los dos números como dividendo. Usa el menor de los dos números como divisor. Configure una ecuación en forma de cociente-resto para estos dos números.
3 Usa el mayor de los dos números como dividendo. Usa el menor de los dos números como divisor. Configure una ecuación en forma de cociente-resto para estos dos números. - Por ejemplo, si está tratando de encontrar el mínimo común múltiplo de 210 y 45, debería calcular .
-
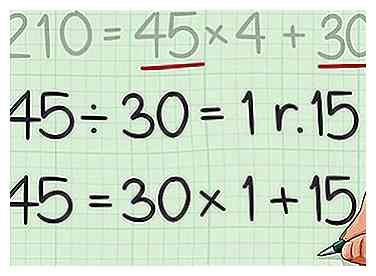 4 Usa el divisor original como el nuevo dividendo. Use el resto como el nuevo divisor. Configure una ecuación en forma de cociente-resto para estos dos números.
4 Usa el divisor original como el nuevo dividendo. Use el resto como el nuevo divisor. Configure una ecuación en forma de cociente-resto para estos dos números. - Por ejemplo, .
-
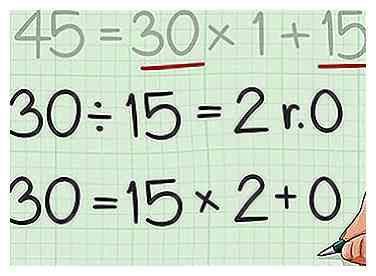 5 Repite este proceso hasta que tengas un resto de 0. Para cada nueva ecuación, utilice el divisor de la ecuación anterior como el nuevo dividendo y el resto anterior como el nuevo divisor.[10]
5 Repite este proceso hasta que tengas un resto de 0. Para cada nueva ecuación, utilice el divisor de la ecuación anterior como el nuevo dividendo y el resto anterior como el nuevo divisor.[10] - Por ejemplo, . Como el resto es 0, no necesita dividir más.
-
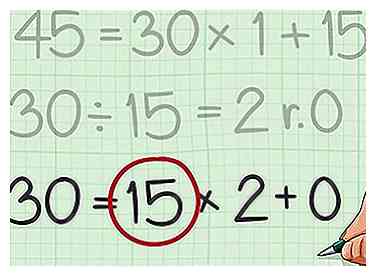 6 Mira el último divisor que usaste. Este es el mayor divisor común para los dos números.[11]
6 Mira el último divisor que usaste. Este es el mayor divisor común para los dos números.[11] - Por ejemplo, desde la última ecuación fue , el último divisor tenía 15, y por eso 15 es el mayor divisor común de 210 y 45.
-
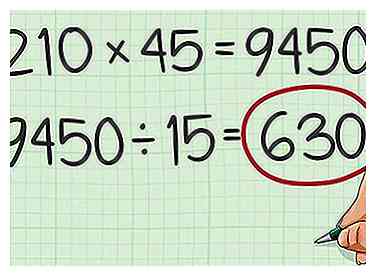 7 Multiplica los dos números. Divida el producto por el mayor divisor común. Esto le dará el mínimo común múltiplo de los dos números.[12]
7 Multiplica los dos números. Divida el producto por el mayor divisor común. Esto le dará el mínimo común múltiplo de los dos números.[12] - Por ejemplo, . Dividiendo por el mayor divisor común, obtienes . Entonces, 630 es el múltiplo menos común de 210 y 45.
 Minotauromaquia
Minotauromaquia
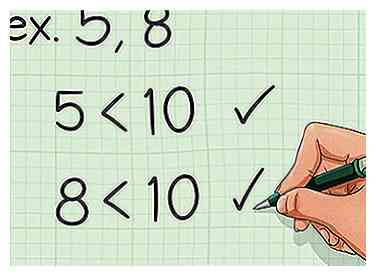 1 Evalúa tus números Este método funciona mejor cuando trabaja con dos números que son menos de 10. Si trabaja con números más grandes, lo mejor es usar un método diferente.
1 Evalúa tus números Este método funciona mejor cuando trabaja con dos números que son menos de 10. Si trabaja con números más grandes, lo mejor es usar un método diferente.  2 Escriba los primeros varios múltiplos del primer número. Un múltiplo es un producto de cualquier número y entero.[1] En otras palabras, son los números que verías en una tabla de multiplicar.
2 Escriba los primeros varios múltiplos del primer número. Un múltiplo es un producto de cualquier número y entero.[1] En otras palabras, son los números que verías en una tabla de multiplicar.  3 Escriba los primeros varios múltiplos del segundo número. Haga esto cerca del primer conjunto de múltiplos, para que sean fáciles de comparar.
3 Escriba los primeros varios múltiplos del segundo número. Haga esto cerca del primer conjunto de múltiplos, para que sean fáciles de comparar.  4 Encuentra el múltiplo más pequeño que los números tienen en común. Es posible que deba extender su lista de múltiplos hasta que encuentre una que ambos comparten. Este número será su múltiplo menos común.[2]
4 Encuentra el múltiplo más pequeño que los números tienen en común. Es posible que deba extender su lista de múltiplos hasta que encuentre una que ambos comparten. Este número será su múltiplo menos común.[2] 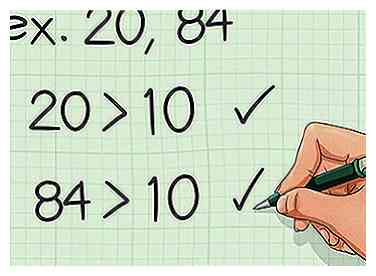 1 Evalúa tus números Este método funciona mejor cuando los números con los que está trabajando son mayores que 10. Si tiene números más pequeños, puede usar un método diferente para encontrar el múltiplo menos común más rápidamente.
1 Evalúa tus números Este método funciona mejor cuando los números con los que está trabajando son mayores que 10. Si tiene números más pequeños, puede usar un método diferente para encontrar el múltiplo menos común más rápidamente. 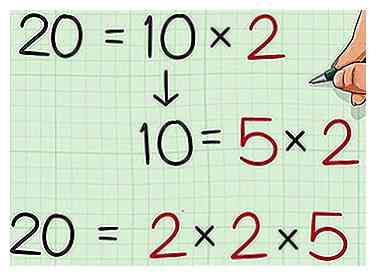 2 Factoriza el primer número. Desea factorizar el número en sus factores primos; es decir, encuentre los factores principales que puede multiplicar para obtener este número. Una forma de hacerlo es creando un árbol de factores. Una vez que haya terminado de factorizar, vuelva a escribir los factores primos como una ecuación.
2 Factoriza el primer número. Desea factorizar el número en sus factores primos; es decir, encuentre los factores principales que puede multiplicar para obtener este número. Una forma de hacerlo es creando un árbol de factores. Una vez que haya terminado de factorizar, vuelva a escribir los factores primos como una ecuación. 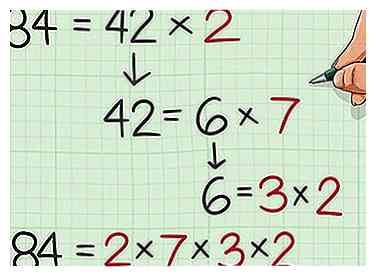 3 Factoriza el segundo número. Haga esto de la misma manera que factorizó el primer número, encontrando los factores primos que puede multiplicar juntos para obtener el número.
3 Factoriza el segundo número. Haga esto de la misma manera que factorizó el primer número, encontrando los factores primos que puede multiplicar juntos para obtener el número. 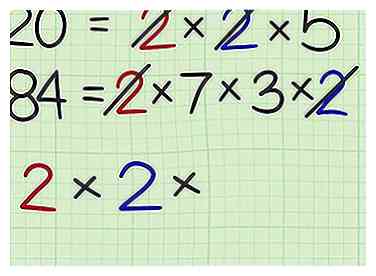 4 Escriba los factores que cada número comparte. Escribe los factores como una oración de multiplicación. A medida que escribe cada factor, sepárelo en cada ecuación de factorización de los números.
4 Escriba los factores que cada número comparte. Escribe los factores como una oración de multiplicación. A medida que escribe cada factor, sepárelo en cada ecuación de factorización de los números. 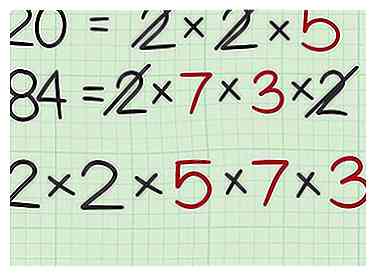 5 Agregue los factores sobrantes a la oración de multiplicación. Estos son los factores que no tachó cuando comparó los dos grupos de factores. Por lo tanto, estos son factores que los dos números no comparten.[3]
5 Agregue los factores sobrantes a la oración de multiplicación. Estos son los factores que no tachó cuando comparó los dos grupos de factores. Por lo tanto, estos son factores que los dos números no comparten.[3] 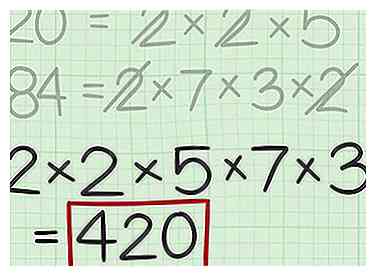 6 Calcula el mínimo común múltiplo. Para hacer esto, multiplica todos los factores en tu oración de multiplicación.
6 Calcula el mínimo común múltiplo. Para hacer esto, multiplica todos los factores en tu oración de multiplicación.  1 Dibuja una cuadrícula de tres en raya. Una cuadrícula tic-tac-toe es dos conjuntos de líneas paralelas que se intersectan perpendicularmente. Las líneas forman tres filas y tres columnas y se parecen a la tecla numeral (#) en un teléfono o teclado. Escribe tu primer número en el cuadrado superior central de la grilla. Escribe tu segundo número en el recuadro superior derecho de la grilla.[4]
1 Dibuja una cuadrícula de tres en raya. Una cuadrícula tic-tac-toe es dos conjuntos de líneas paralelas que se intersectan perpendicularmente. Las líneas forman tres filas y tres columnas y se parecen a la tecla numeral (#) en un teléfono o teclado. Escribe tu primer número en el cuadrado superior central de la grilla. Escribe tu segundo número en el recuadro superior derecho de la grilla.[4]  2 Busque un factor que sea común a ambos números. Escribe este número en el cuadrado superior izquierdo de tu grilla. Es útil usar factores primos, pero no necesariamente es necesario.
2 Busque un factor que sea común a ambos números. Escribe este número en el cuadrado superior izquierdo de tu grilla. Es útil usar factores primos, pero no necesariamente es necesario.  3 Divide el factor en cada número. Escribe el cociente en el cuadrado debajo de cualquier número. Un cociente es la respuesta a un problema de división.
3 Divide el factor en cada número. Escribe el cociente en el cuadrado debajo de cualquier número. Un cociente es la respuesta a un problema de división.  4 Encuentre un factor que sea común a los dos cocientes. Si no hay un factor común para ambos cocientes, puede omitir este y el siguiente paso. Si hay un factor común, escríbalo en el recuadro de la mitad izquierda de la cuadrícula.
4 Encuentre un factor que sea común a los dos cocientes. Si no hay un factor común para ambos cocientes, puede omitir este y el siguiente paso. Si hay un factor común, escríbalo en el recuadro de la mitad izquierda de la cuadrícula.  5 Divida este nuevo factor en cada cociente. Escribe este nuevo cociente debajo de los primeros.
5 Divida este nuevo factor en cada cociente. Escribe este nuevo cociente debajo de los primeros.  6 Extiende tu grilla si es necesario. Siga este mismo proceso hasta llegar a un punto donde el último conjunto de cocientes no tenga un factor en común.
6 Extiende tu grilla si es necesario. Siga este mismo proceso hasta llegar a un punto donde el último conjunto de cocientes no tenga un factor en común.  7 Dibuja un círculo alrededor de los números en la primera columna y la última fila de tu grilla. Puedes pensar que está dibujando una "L" para "múltiplo mínimo común". Escribe una oración de multiplicación usando todos estos factores.[5]
7 Dibuja un círculo alrededor de los números en la primera columna y la última fila de tu grilla. Puedes pensar que está dibujando una "L" para "múltiplo mínimo común". Escribe una oración de multiplicación usando todos estos factores.[5] 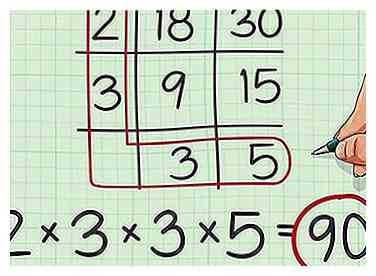 8 Completa la multiplicación. Cuando multiplicas todos estos factores juntos, el resultado es el múltiplo menos común de tus dos números originales.[6]
8 Completa la multiplicación. Cuando multiplicas todos estos factores juntos, el resultado es el múltiplo menos común de tus dos números originales.[6]  1 Comprende el vocabulario de la división. El dividendo es el número que se divide. El divisor es el número por el que se divide el dividendo. El cociente es la respuesta al problema de la división. El resto es la cantidad que queda después de que un número se divide por otro.[7]
1 Comprende el vocabulario de la división. El dividendo es el número que se divide. El divisor es el número por el que se divide el dividendo. El cociente es la respuesta al problema de la división. El resto es la cantidad que queda después de que un número se divide por otro.[7] 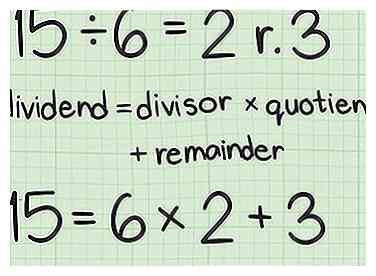 2 Configure la fórmula para el formulario cociente-resto. La fórmula es
2 Configure la fórmula para el formulario cociente-resto. La fórmula es 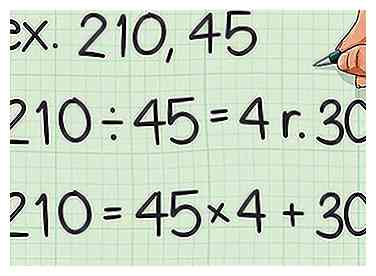 3 Usa el mayor de los dos números como dividendo. Usa el menor de los dos números como divisor. Configure una ecuación en forma de cociente-resto para estos dos números.
3 Usa el mayor de los dos números como dividendo. Usa el menor de los dos números como divisor. Configure una ecuación en forma de cociente-resto para estos dos números. 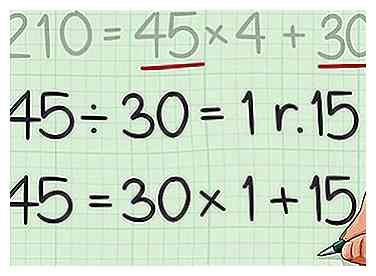 4 Usa el divisor original como el nuevo dividendo. Use el resto como el nuevo divisor. Configure una ecuación en forma de cociente-resto para estos dos números.
4 Usa el divisor original como el nuevo dividendo. Use el resto como el nuevo divisor. Configure una ecuación en forma de cociente-resto para estos dos números. 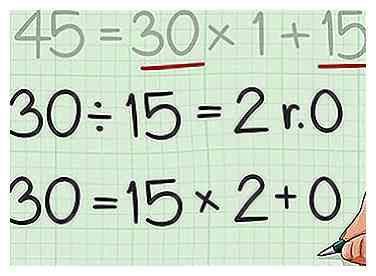 5 Repite este proceso hasta que tengas un resto de 0. Para cada nueva ecuación, utilice el divisor de la ecuación anterior como el nuevo dividendo y el resto anterior como el nuevo divisor.[10]
5 Repite este proceso hasta que tengas un resto de 0. Para cada nueva ecuación, utilice el divisor de la ecuación anterior como el nuevo dividendo y el resto anterior como el nuevo divisor.[10] 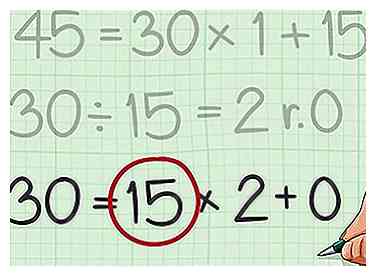 6 Mira el último divisor que usaste. Este es el mayor divisor común para los dos números.[11]
6 Mira el último divisor que usaste. Este es el mayor divisor común para los dos números.[11] 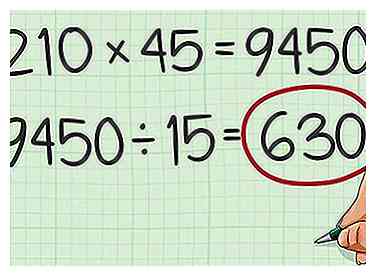 7 Multiplica los dos números. Divida el producto por el mayor divisor común. Esto le dará el mínimo común múltiplo de los dos números.[12]
7 Multiplica los dos números. Divida el producto por el mayor divisor común. Esto le dará el mínimo común múltiplo de los dos números.[12]