Cuando dos variables son directamente proporcionales, cambian a la misma velocidad. La tasa se muestra por la constante en la ecuación . Las variables directamente proporcionales se indican gráficamente mediante una línea recta que pasa por el origen del plano de coordenadas. Una vez que comprende estos conceptos básicos, es fácil identificar variables directamente proporcionales usando la ecuación de su línea o sus valores.
Método uno de cuatro:
Reescribiendo la ecuación de la línea
-
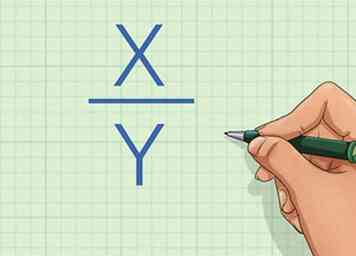 1 Comprender la proporción directa. Dos variables están en proporción directa si cada variable cambia a la misma velocidad.[1] En otras palabras, si cambios por un cierto factor o constante (), entonces cambios por esa misma constante ().
1 Comprender la proporción directa. Dos variables están en proporción directa si cada variable cambia a la misma velocidad.[1] En otras palabras, si cambios por un cierto factor o constante (), entonces cambios por esa misma constante (). -
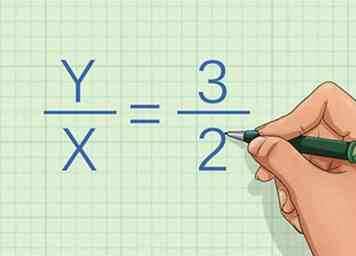 2 Escriba la ecuación de la línea. La ecuación tendrá dos variables y una constante. Si no le dan la ecuación, no puede usar este método.
2 Escriba la ecuación de la línea. La ecuación tendrá dos variables y una constante. Si no le dan la ecuación, no puede usar este método. - Por ejemplo, se te puede dar la ecuación .
-
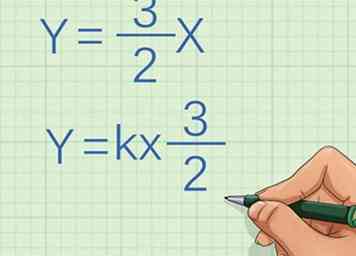 3 Reescribe la ecuación en forma de proporción directa o variación. La ecuación es , dónde es igual a la coordenada y de un punto en la línea, es igual a la coordenada x para ese mismo punto, y es la constante o pendiente de la línea. Usa álgebra para reordenar la ecuación en forma de . Si no puede reescribir la ecuación en esta forma, las variables no son directamente proporcionales. Si puede, prueba que son directamente proporcionales.[2]
3 Reescribe la ecuación en forma de proporción directa o variación. La ecuación es , dónde es igual a la coordenada y de un punto en la línea, es igual a la coordenada x para ese mismo punto, y es la constante o pendiente de la línea. Usa álgebra para reordenar la ecuación en forma de . Si no puede reescribir la ecuación en esta forma, las variables no son directamente proporcionales. Si puede, prueba que son directamente proporcionales.[2] - Por ejemplo, si multiplicas ambos lados de la ecuación por , la ecuación se vuelve , que está en la forma de , con siendo la constante.
Método dos de cuatro:
Usando un conjunto de puntos
-
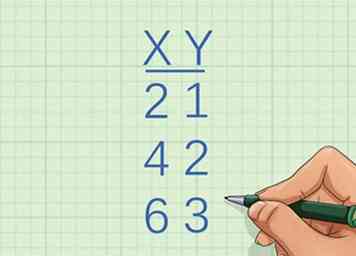 1 Identifica las coordenadas x de los dos primeros puntos. Debería recibir una lista de coordenadas o un gráfico del que puede determinar las coordenadas de los puntos. Si no tiene las coordenadas de puntos en la línea, no puede usar este método.
1 Identifica las coordenadas x de los dos primeros puntos. Debería recibir una lista de coordenadas o un gráfico del que puede determinar las coordenadas de los puntos. Si no tiene las coordenadas de puntos en la línea, no puede usar este método. - Por ejemplo, se le puede dar el conjunto de puntos
- La coordenada x del primer punto es 2, y la coordenada x del segundo punto es 4.
-
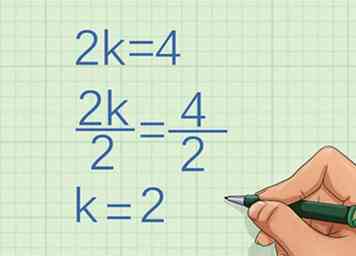 2 Determine el factor por el cual la variable crece Para hacer esto, determine qué factor, o constante, se multiplica por la primera coordenada x para llegar a la segunda coordenada.
2 Determine el factor por el cual la variable crece Para hacer esto, determine qué factor, o constante, se multiplica por la primera coordenada x para llegar a la segunda coordenada. - Por ejemplo, si la primera coordenada x es 2, y la segunda coordenada x es 4, debe determinar qué multiplicar 2 por para obtener 4:
Entonces el la variable crece por la constante 2.
- Por ejemplo, si la primera coordenada x es 2, y la segunda coordenada x es 4, debe determinar qué multiplicar 2 por para obtener 4:
-
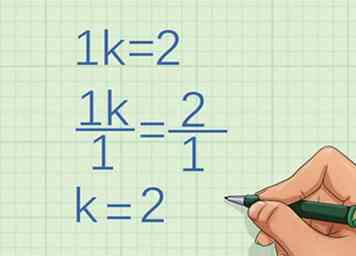 3 Determine el factor por el cual la variable crece Usa los mismos dos puntos que usaste para determinar el crecimiento de . Usa álgebra para determinar el factor por el cual varían las dos coordenadas.
3 Determine el factor por el cual la variable crece Usa los mismos dos puntos que usaste para determinar el crecimiento de . Usa álgebra para determinar el factor por el cual varían las dos coordenadas. - Por ejemplo, si la primera coordenada y es 1, y la segunda coordenada y es 2, necesita determinar lo que multiplica 1 por para obtener 2:
Entonces, la variable crece por la constante 2.
- Por ejemplo, si la primera coordenada y es 1, y la segunda coordenada y es 2, necesita determinar lo que multiplica 1 por para obtener 2:
-
 4 Compara las constantes de las dos variables. Si y cambiado al mismo ritmo, o por el mismo factor, entonces son directamente proporcionales.[3]
4 Compara las constantes de las dos variables. Si y cambiado al mismo ritmo, o por el mismo factor, entonces son directamente proporcionales.[3] - Por ejemplo, dado que las coordenadas x cambiaron por un factor de 2 mientras que las coordenadas y también cambiaron por un factor de 2, las dos variables son directamente proporcionales.
Método tres de cuatro:
Usando un gráfico
-
 1 Tenga en cuenta si la línea es recta. Cuando dos variables están en proporción, la línea que las representa será recta.[4] Esto significa que la pendiente de la línea es constante o sigue la ecuación .
1 Tenga en cuenta si la línea es recta. Cuando dos variables están en proporción, la línea que las representa será recta.[4] Esto significa que la pendiente de la línea es constante o sigue la ecuación . -
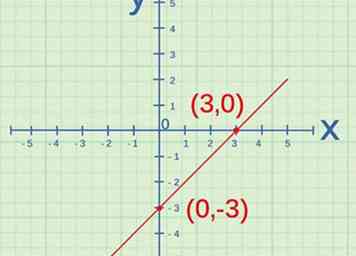 2 Determine la intersección con el eje y La intersección con el eje y es el punto donde la línea cruza el eje y. Cuando dos variables son directamente proporcionales, cuando se grafican, su línea cruzará el origen. El origen está en el punto , entonces la intersección en y de la línea debería ser . Si no es así, las variables no son directamente proporcionales.[5]
2 Determine la intersección con el eje y La intersección con el eje y es el punto donde la línea cruza el eje y. Cuando dos variables son directamente proporcionales, cuando se grafican, su línea cruzará el origen. El origen está en el punto , entonces la intersección en y de la línea debería ser . Si no es así, las variables no son directamente proporcionales.[5] - El eje y es el eje vertical.
-
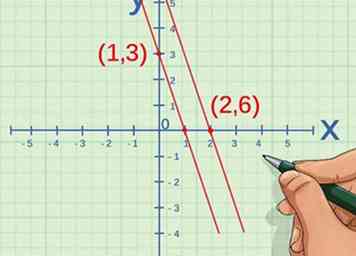 3 Encuentra las coordenadas de dos puntos en la línea. Compare las coordenadas entre sí y determine si cada coordenada cambió por el mismo factor.[6] Es decir, determinar si la constante () es lo mismo para ambos y valores.
3 Encuentra las coordenadas de dos puntos en la línea. Compare las coordenadas entre sí y determine si cada coordenada cambió por el mismo factor.[6] Es decir, determinar si la constante () es lo mismo para ambos y valores. - Por ejemplo, si el primer punto es , y el segundo punto es , la coordenada x cambia por un factor de 2, ya que . La coordenada y también cambió por un factor de 2, ya que . Por lo tanto, puede confirmar que la línea representa dos variables que son directamente proporcionales.
Método cuatro de cuatro:
Completando problemas de muestra
-
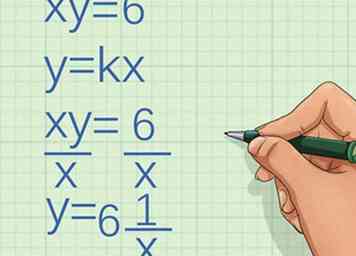 1 Mira la ecuación. Determine si las dos variables son directamente proporcionales: .
1 Mira la ecuación. Determine si las dos variables son directamente proporcionales: . - Recuerde que si las variables son directamente proporcionales, seguirán el patrón .
- Usa álgebra para reescribir la ecuación.
- Aislar el variable dividiendo cada lado por :
- Aislar el variable dividiendo cada lado por :
- Evaluar si la ecuación reescrita sigue el patrón . En este caso, la ecuación no, por lo que las variables no son directamente proporcionales. De hecho, son inversamente proporcionales.[7]
-
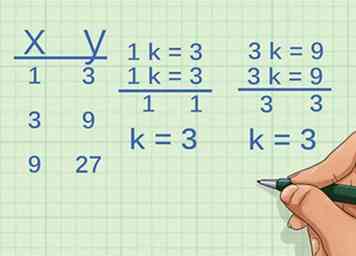 2 Considera el siguiente conjunto de puntos. ¿Las variables son directamente proporcionales?
2 Considera el siguiente conjunto de puntos. ¿Las variables son directamente proporcionales?
- Determine el crecimiento de . Para ello, encuentre el factor por el que multiplica la primera coordenada x por llegar a la segunda coordenada:
Entonces, la coordenada x crece por factor de 3. - Determine el crecimiento de :
Entonces, la coordenada y crece por factor de 3. - Compara el factor, o constante, de las dos variables. Ambos crecen por un factor de 3. Por lo tanto, las variables son directamente proporcionales.
- Determine el crecimiento de . Para ello, encuentre el factor por el que multiplica la primera coordenada x por llegar a la segunda coordenada:
-
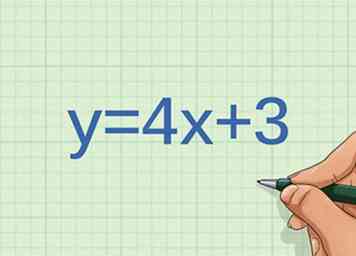 3 Considera un gráfico de la línea . ¿El gráfico muestra la proporción directa entre las variables?
3 Considera un gráfico de la línea . ¿El gráfico muestra la proporción directa entre las variables? - Tenga en cuenta si la línea es recta. Como la ecuación de la línea está en forma de pendiente-intersección, tiene una pendiente constante, lo que significa que la línea es recta. Tan potencialmente, las variables son directamente proporcionales.
- Determine la intersección con el eje y Si las variables son directamente proporcionales, la línea pasará por el punto . La intersección en y de esta línea es el punto . Entonces, las variables no son directamente proporcionales.
 Minotauromaquia
Minotauromaquia
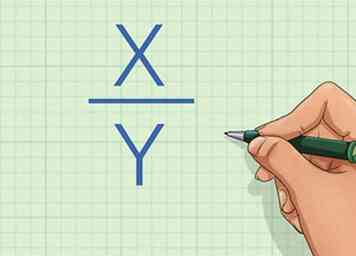 1 Comprender la proporción directa. Dos variables están en proporción directa si cada variable cambia a la misma velocidad.[1] En otras palabras, si
1 Comprender la proporción directa. Dos variables están en proporción directa si cada variable cambia a la misma velocidad.[1] En otras palabras, si 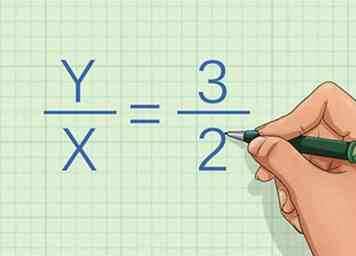 2 Escriba la ecuación de la línea. La ecuación tendrá dos variables y una constante. Si no le dan la ecuación, no puede usar este método.
2 Escriba la ecuación de la línea. La ecuación tendrá dos variables y una constante. Si no le dan la ecuación, no puede usar este método. 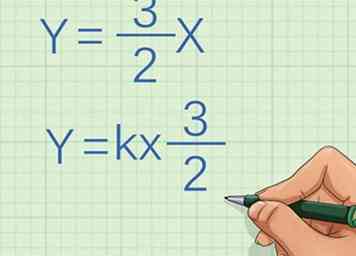 3 Reescribe la ecuación en forma de proporción directa o variación. La ecuación es
3 Reescribe la ecuación en forma de proporción directa o variación. La ecuación es  1 Identifica las coordenadas x de los dos primeros puntos. Debería recibir una lista de coordenadas o un gráfico del que puede determinar las coordenadas de los puntos. Si no tiene las coordenadas de puntos en la línea, no puede usar este método.
1 Identifica las coordenadas x de los dos primeros puntos. Debería recibir una lista de coordenadas o un gráfico del que puede determinar las coordenadas de los puntos. Si no tiene las coordenadas de puntos en la línea, no puede usar este método. 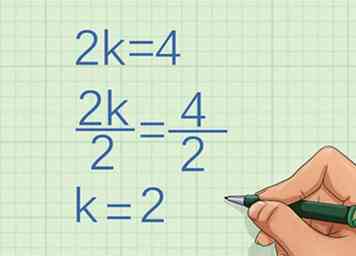 2 Determine el factor por el cual
2 Determine el factor por el cual 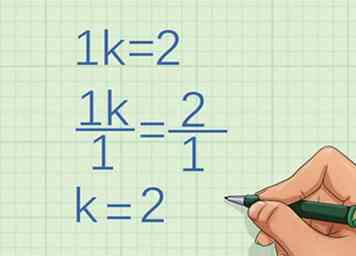 3 Determine el factor por el cual
3 Determine el factor por el cual  4 Compara las constantes de las dos variables. Si
4 Compara las constantes de las dos variables. Si  1 Tenga en cuenta si la línea es recta. Cuando dos variables están en proporción, la línea que las representa será recta.[4] Esto significa que la pendiente de la línea es constante o sigue la ecuación
1 Tenga en cuenta si la línea es recta. Cuando dos variables están en proporción, la línea que las representa será recta.[4] Esto significa que la pendiente de la línea es constante o sigue la ecuación  2 Determine la intersección con el eje y La intersección con el eje y es el punto donde la línea cruza el eje y. Cuando dos variables son directamente proporcionales, cuando se grafican, su línea cruzará el origen. El origen está en el punto
2 Determine la intersección con el eje y La intersección con el eje y es el punto donde la línea cruza el eje y. Cuando dos variables son directamente proporcionales, cuando se grafican, su línea cruzará el origen. El origen está en el punto  3 Encuentra las coordenadas de dos puntos en la línea. Compare las coordenadas entre sí y determine si cada coordenada cambió por el mismo factor.[6] Es decir, determinar si la constante (
3 Encuentra las coordenadas de dos puntos en la línea. Compare las coordenadas entre sí y determine si cada coordenada cambió por el mismo factor.[6] Es decir, determinar si la constante (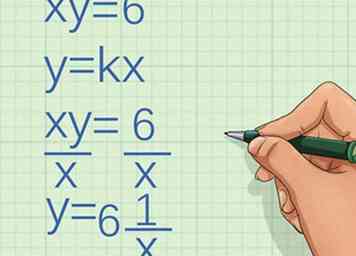 1 Mira la ecuación. Determine si las dos variables son directamente proporcionales:
1 Mira la ecuación. Determine si las dos variables son directamente proporcionales: 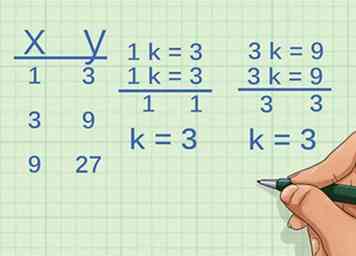 2 Considera el siguiente conjunto de puntos. ¿Las variables son directamente proporcionales?
2 Considera el siguiente conjunto de puntos. ¿Las variables son directamente proporcionales?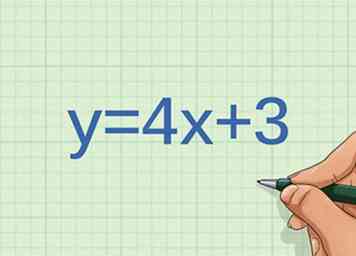 3 Considera un gráfico de la línea
3 Considera un gráfico de la línea