El rango de una función es el conjunto de números que la función puede producir. En otras palabras, es el conjunto de valores y que obtiene cuando conecta todos los posibles valores x en la función. Este conjunto de posibles valores x se llama dominio. Si quieres saber cómo encontrar el rango de una función, solo sigue estos pasos.
Método uno de cuatro:
Encontrar el rango de una función dada una fórmula
-
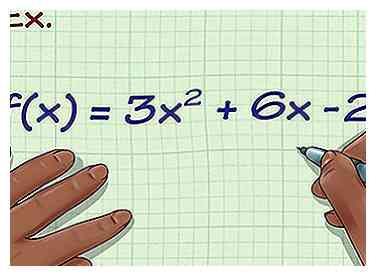 1 Escriba la fórmula. Supongamos que la fórmula con la que está trabajando es la siguiente: f (x) = 3x2 + 6x -2. Esto significa que cuando coloca cualquier X en la ecuación, obtendrás tu y valor. Esta es la función de una parábola.
1 Escriba la fórmula. Supongamos que la fórmula con la que está trabajando es la siguiente: f (x) = 3x2 + 6x -2. Esto significa que cuando coloca cualquier X en la ecuación, obtendrás tu y valor. Esta es la función de una parábola. -
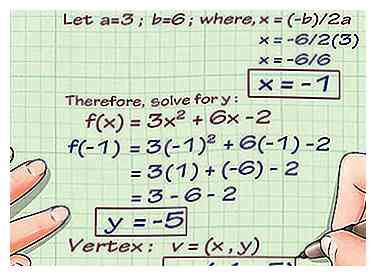 2 Encuentra el vértice de la función si es cuadrática. Si está trabajando con una línea recta o cualquier función con un polinomio de un número impar, como f (x) = 6x3+ 2x + 7, puede omitir este paso. Pero si estás trabajando con una parábola, o cualquier ecuación donde la coordenada x se cuadra o se eleva a una potencia par, tendrás que trazar el vértice. Para hacer esto, solo usa la fórmula -b / 2a para obtener la coordenada x de la función 3x2 + 6x -2, donde 3 = a, 6 = b, y -2 = c. En este caso -segundo es -6, y 2a es 6, entonces la coordenada x es -6/6, o -1.
2 Encuentra el vértice de la función si es cuadrática. Si está trabajando con una línea recta o cualquier función con un polinomio de un número impar, como f (x) = 6x3+ 2x + 7, puede omitir este paso. Pero si estás trabajando con una parábola, o cualquier ecuación donde la coordenada x se cuadra o se eleva a una potencia par, tendrás que trazar el vértice. Para hacer esto, solo usa la fórmula -b / 2a para obtener la coordenada x de la función 3x2 + 6x -2, donde 3 = a, 6 = b, y -2 = c. En este caso -segundo es -6, y 2a es 6, entonces la coordenada x es -6/6, o -1. - Ahora, enchufe -1 en la función para obtener la coordenada y. f (-1) = 3 (-1)2 + 6(-1) -2 = 3 - 6 -2 = -5.
- El vértice es (-1, -5). Represéntalo dibujando un punto donde la coordenada x es -1 y donde la coordenada y es -5. Debería estar en el tercer cuadrante del gráfico.
-
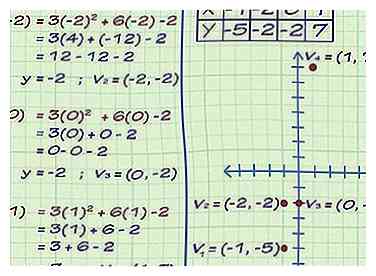 3 Encuentra algunos otros puntos en la función. Para tener una idea de la función, debe conectar algunas otras coordenadas x para que pueda tener una idea de cómo se ve la función antes de comenzar a buscar el rango. Como es una parábola y la x2 la coordenada es positiva, estará apuntando hacia arriba. Pero solo para cubrir tus bases, conectemos algunas coordenadas x para ver qué y coordinan:
3 Encuentra algunos otros puntos en la función. Para tener una idea de la función, debe conectar algunas otras coordenadas x para que pueda tener una idea de cómo se ve la función antes de comenzar a buscar el rango. Como es una parábola y la x2 la coordenada es positiva, estará apuntando hacia arriba. Pero solo para cubrir tus bases, conectemos algunas coordenadas x para ver qué y coordinan: - f (-2) = 3 (-2)2 + 6 (-2) -2 = -2. Un punto en el gráfico es (-2, -2)
- f (0) = 3 (0)2 + 6 (0) -2 = -2. Otro punto en el gráfico es (0, -2)
- f (1) = 3 (1)2 + 6 (1) -2 = 7. Un tercer punto en el gráfico es (1, 7).
-
 4 Encuentra el rango en el gráfico. Ahora, mira las coordenadas y en el gráfico y encuentra el punto más bajo en el que el gráfico toca una coordenada y. En este caso, la coordenada y más baja está en el vértice, -5, y el gráfico se extiende infinitamente por encima de este punto. Esto significa que el rango de la función es y = todos los números reales ≥ -5.
4 Encuentra el rango en el gráfico. Ahora, mira las coordenadas y en el gráfico y encuentra el punto más bajo en el que el gráfico toca una coordenada y. En este caso, la coordenada y más baja está en el vértice, -5, y el gráfico se extiende infinitamente por encima de este punto. Esto significa que el rango de la función es y = todos los números reales ≥ -5.
Método dos de cuatro:
Encontrar el rango de una función en un gráfico
-
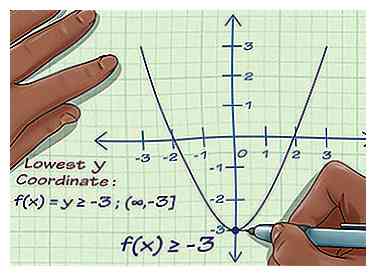 1 Encuentra el mínimo de la función. Busque la coordenada y más baja de la función. Digamos que la función alcanza su punto más bajo en -3. Esta función también podría hacerse más pequeña y más pequeña infinitamente, de modo que no tenga un punto más bajo establecido, solo infinito.
1 Encuentra el mínimo de la función. Busque la coordenada y más baja de la función. Digamos que la función alcanza su punto más bajo en -3. Esta función también podría hacerse más pequeña y más pequeña infinitamente, de modo que no tenga un punto más bajo establecido, solo infinito. -
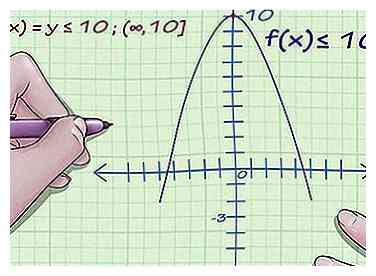 2 Encuentra el máximo de la función. Digamos que la coordenada y más alta que alcanza la función es 10. Esta función también podría hacerse más grande y más grande infinitamente, por lo que no tiene un punto alto establecido, solo infinito.
2 Encuentra el máximo de la función. Digamos que la coordenada y más alta que alcanza la función es 10. Esta función también podría hacerse más grande y más grande infinitamente, por lo que no tiene un punto alto establecido, solo infinito. -
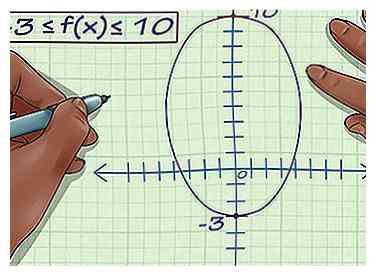 3 Indique el rango. Esto significa que el rango de la función, o el rango de coordenadas y, varía de -3 a 10. Entonces, -3 ≤ f (x) ≤ 10. Ese es el rango de la función.
3 Indique el rango. Esto significa que el rango de la función, o el rango de coordenadas y, varía de -3 a 10. Entonces, -3 ≤ f (x) ≤ 10. Ese es el rango de la función. - Pero digamos que el gráfico alcanza su punto más bajo en y = -3, pero va hacia arriba para siempre. Entonces el rango es f (x) ≥ -3 y eso es todo.
- Digamos que el gráfico alcanza su punto más alto en 10, pero va hacia abajo para siempre. Entonces el rango es f (x) ≤ 10.
Método tres de cuatro:
Encontrar el rango de una función de una relación
-
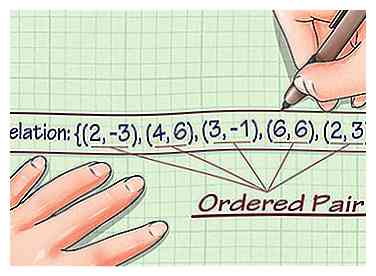 1 Escriba la relación. Una relación es un conjunto de pares ordenados con coordenadas xey. Puede ver una relación y determinar su dominio y rango. Supongamos que está trabajando con la siguiente relación: (2, -3), (4, 6), (3, -1), (6, 6), (2, 3).[1]
1 Escriba la relación. Una relación es un conjunto de pares ordenados con coordenadas xey. Puede ver una relación y determinar su dominio y rango. Supongamos que está trabajando con la siguiente relación: (2, -3), (4, 6), (3, -1), (6, 6), (2, 3).[1] -
 2 Enumera las coordenadas y de la relación. Para encontrar el rango de la relación, simplemente anote todas las coordenadas y de cada par ordenado: -3, 6, -1, 6, 3.[2]
2 Enumera las coordenadas y de la relación. Para encontrar el rango de la relación, simplemente anote todas las coordenadas y de cada par ordenado: -3, 6, -1, 6, 3.[2] -
 3 Elimine las coordenadas duplicadas para que solo tenga una de cada coordenada y. Notarás que has enlistado "6" dos veces. Sácalo para que te quede -3, -1, 6, 3.[3]
3 Elimine las coordenadas duplicadas para que solo tenga una de cada coordenada y. Notarás que has enlistado "6" dos veces. Sácalo para que te quede -3, -1, 6, 3.[3] -
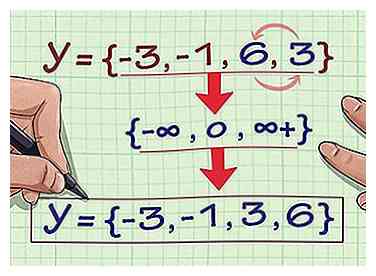 4 Escribe el rango de la relación en orden ascendente. Ahora, reordene los números en el conjunto para que se mueva del más pequeño al más grande, y usted tiene su rango. El rango de la relación (2, -3), (4, 6), (3, -1), (6, 6), (2, 3) es -3, -1, 3, 6 . Ya has terminado.[4]
4 Escribe el rango de la relación en orden ascendente. Ahora, reordene los números en el conjunto para que se mueva del más pequeño al más grande, y usted tiene su rango. El rango de la relación (2, -3), (4, 6), (3, -1), (6, 6), (2, 3) es -3, -1, 3, 6 . Ya has terminado.[4] -
 5 Asegúrate de que la relación es Una función. Para que una relación sea una función, cada vez que ingresas un número de una coordenada x, la coordenada y tiene que ser la misma. Por ejemplo, la relación (2, 3) (2, 4) (6, 9) es no una función, porque cuando pones 2 como una x la primera vez, obtienes un 3, pero la segunda vez que pones un 2, obtienes un cuatro. Para que una relación sea una función, si pones la misma entrada, siempre deberías obtener el mismo resultado. Si coloca un -7, debe obtener la misma coordenada y (cualquiera que sea) cada vez.[5]
5 Asegúrate de que la relación es Una función. Para que una relación sea una función, cada vez que ingresas un número de una coordenada x, la coordenada y tiene que ser la misma. Por ejemplo, la relación (2, 3) (2, 4) (6, 9) es no una función, porque cuando pones 2 como una x la primera vez, obtienes un 3, pero la segunda vez que pones un 2, obtienes un cuatro. Para que una relación sea una función, si pones la misma entrada, siempre deberías obtener el mismo resultado. Si coloca un -7, debe obtener la misma coordenada y (cualquiera que sea) cada vez.[5]
Método cuatro de cuatro:
Encontrar el rango de una función en un problema de Word
-
 1 Lee el problema Digamos que estás trabajando con el siguiente problema: "Becky está vendiendo boletos para el concurso de talentos de su escuela por 5 dólares cada uno. La cantidad de dinero que recauda es una función de la cantidad de boletos que vende. ¿Cuál es el rango de la función?"
1 Lee el problema Digamos que estás trabajando con el siguiente problema: "Becky está vendiendo boletos para el concurso de talentos de su escuela por 5 dólares cada uno. La cantidad de dinero que recauda es una función de la cantidad de boletos que vende. ¿Cuál es el rango de la función?" -
 2 Escribe el problema como una función. En este caso, METRO representa la cantidad de dinero que recauda, y t representa la cantidad de boletos que ella vende.Sin embargo, dado que cada boleto costará 5 dólares, tendrá que multiplicar la cantidad de boletos vendidos por 5 para encontrar la cantidad de dinero. Por lo tanto, la función se puede escribir como M (t) = 5t.
2 Escribe el problema como una función. En este caso, METRO representa la cantidad de dinero que recauda, y t representa la cantidad de boletos que ella vende.Sin embargo, dado que cada boleto costará 5 dólares, tendrá que multiplicar la cantidad de boletos vendidos por 5 para encontrar la cantidad de dinero. Por lo tanto, la función se puede escribir como M (t) = 5t. - Por ejemplo, si vende 2 boletos, tendrá que multiplicar 2 por 5 para obtener 10, la cantidad de dólares que obtendrá.
-
 3 Determine el dominio Para determinar el rango, primero debe encontrar el dominio. El dominio es todos los valores posibles de t que funcionan en la ecuación. En este caso, Becky puede vender 0 o más boletos: no puede vender boletos negativos. Dado que no conocemos el número de escaños en el auditorio de su escuela, podemos suponer que teóricamente puede vender un número infinito de boletos. Y ella solo puede vender boletos enteros; ella no puede vender 1/2 de un boleto, por ejemplo. Por lo tanto, el dominio de la función es t = cualquier entero no negativo.
3 Determine el dominio Para determinar el rango, primero debe encontrar el dominio. El dominio es todos los valores posibles de t que funcionan en la ecuación. En este caso, Becky puede vender 0 o más boletos: no puede vender boletos negativos. Dado que no conocemos el número de escaños en el auditorio de su escuela, podemos suponer que teóricamente puede vender un número infinito de boletos. Y ella solo puede vender boletos enteros; ella no puede vender 1/2 de un boleto, por ejemplo. Por lo tanto, el dominio de la función es t = cualquier entero no negativo. -
 4 Determine el rango. El rango es la cantidad de dinero posible que Becky puede obtener de su venta. Tienes que trabajar con el dominio para encontrar el rango. Si sabe que el dominio es un entero no negativo y que la fórmula es M (t) = 5t, entonces sabes que puedes conectar cualquier entero no negativo en esta función para obtener la salida o el rango. Por ejemplo, si vende 5 boletos, entonces M (5) = 5 x 5 o 25 dólares. Si ella vende 100, entonces M (100) = 5 x 100 o 500 dólares. Por lo tanto, el rango de la función es cualquier entero no negativo que es un múltiplo de cinco.
4 Determine el rango. El rango es la cantidad de dinero posible que Becky puede obtener de su venta. Tienes que trabajar con el dominio para encontrar el rango. Si sabe que el dominio es un entero no negativo y que la fórmula es M (t) = 5t, entonces sabes que puedes conectar cualquier entero no negativo en esta función para obtener la salida o el rango. Por ejemplo, si vende 5 boletos, entonces M (5) = 5 x 5 o 25 dólares. Si ella vende 100, entonces M (100) = 5 x 100 o 500 dólares. Por lo tanto, el rango de la función es cualquier entero no negativo que es un múltiplo de cinco. - Eso significa que cualquier entero no negativo que sea un múltiplo de cinco es una salida posible para la entrada de la función.
 Minotauromaquia
Minotauromaquia
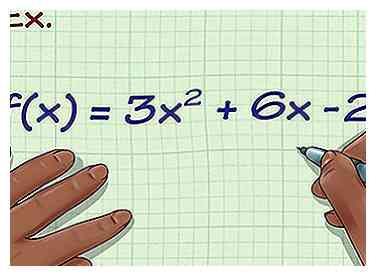 1 Escriba la fórmula. Supongamos que la fórmula con la que está trabajando es la siguiente: f (x) = 3x2 + 6x -2. Esto significa que cuando coloca cualquier X en la ecuación, obtendrás tu y valor. Esta es la función de una parábola.
1 Escriba la fórmula. Supongamos que la fórmula con la que está trabajando es la siguiente: f (x) = 3x2 + 6x -2. Esto significa que cuando coloca cualquier X en la ecuación, obtendrás tu y valor. Esta es la función de una parábola. 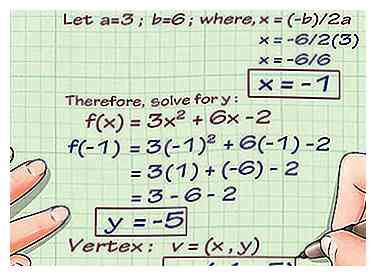 2 Encuentra el vértice de la función si es cuadrática. Si está trabajando con una línea recta o cualquier función con un polinomio de un número impar, como f (x) = 6x3+ 2x + 7, puede omitir este paso. Pero si estás trabajando con una parábola, o cualquier ecuación donde la coordenada x se cuadra o se eleva a una potencia par, tendrás que trazar el vértice. Para hacer esto, solo usa la fórmula -b / 2a para obtener la coordenada x de la función 3x2 + 6x -2, donde 3 = a, 6 = b, y -2 = c. En este caso -segundo es -6, y 2a es 6, entonces la coordenada x es -6/6, o -1.
2 Encuentra el vértice de la función si es cuadrática. Si está trabajando con una línea recta o cualquier función con un polinomio de un número impar, como f (x) = 6x3+ 2x + 7, puede omitir este paso. Pero si estás trabajando con una parábola, o cualquier ecuación donde la coordenada x se cuadra o se eleva a una potencia par, tendrás que trazar el vértice. Para hacer esto, solo usa la fórmula -b / 2a para obtener la coordenada x de la función 3x2 + 6x -2, donde 3 = a, 6 = b, y -2 = c. En este caso -segundo es -6, y 2a es 6, entonces la coordenada x es -6/6, o -1.  3 Encuentra algunos otros puntos en la función. Para tener una idea de la función, debe conectar algunas otras coordenadas x para que pueda tener una idea de cómo se ve la función antes de comenzar a buscar el rango. Como es una parábola y la x2 la coordenada es positiva, estará apuntando hacia arriba. Pero solo para cubrir tus bases, conectemos algunas coordenadas x para ver qué y coordinan:
3 Encuentra algunos otros puntos en la función. Para tener una idea de la función, debe conectar algunas otras coordenadas x para que pueda tener una idea de cómo se ve la función antes de comenzar a buscar el rango. Como es una parábola y la x2 la coordenada es positiva, estará apuntando hacia arriba. Pero solo para cubrir tus bases, conectemos algunas coordenadas x para ver qué y coordinan:  4 Encuentra el rango en el gráfico. Ahora, mira las coordenadas y en el gráfico y encuentra el punto más bajo en el que el gráfico toca una coordenada y. En este caso, la coordenada y más baja está en el vértice, -5, y el gráfico se extiende infinitamente por encima de este punto. Esto significa que el rango de la función es y = todos los números reales ≥ -5.
4 Encuentra el rango en el gráfico. Ahora, mira las coordenadas y en el gráfico y encuentra el punto más bajo en el que el gráfico toca una coordenada y. En este caso, la coordenada y más baja está en el vértice, -5, y el gráfico se extiende infinitamente por encima de este punto. Esto significa que el rango de la función es y = todos los números reales ≥ -5.  1 Encuentra el mínimo de la función. Busque la coordenada y más baja de la función. Digamos que la función alcanza su punto más bajo en -3. Esta función también podría hacerse más pequeña y más pequeña infinitamente, de modo que no tenga un punto más bajo establecido, solo infinito.
1 Encuentra el mínimo de la función. Busque la coordenada y más baja de la función. Digamos que la función alcanza su punto más bajo en -3. Esta función también podría hacerse más pequeña y más pequeña infinitamente, de modo que no tenga un punto más bajo establecido, solo infinito.  2 Encuentra el máximo de la función. Digamos que la coordenada y más alta que alcanza la función es 10. Esta función también podría hacerse más grande y más grande infinitamente, por lo que no tiene un punto alto establecido, solo infinito.
2 Encuentra el máximo de la función. Digamos que la coordenada y más alta que alcanza la función es 10. Esta función también podría hacerse más grande y más grande infinitamente, por lo que no tiene un punto alto establecido, solo infinito.  3 Indique el rango. Esto significa que el rango de la función, o el rango de coordenadas y, varía de -3 a 10. Entonces, -3 ≤ f (x) ≤ 10. Ese es el rango de la función.
3 Indique el rango. Esto significa que el rango de la función, o el rango de coordenadas y, varía de -3 a 10. Entonces, -3 ≤ f (x) ≤ 10. Ese es el rango de la función.  1 Escriba la relación. Una relación es un conjunto de pares ordenados con coordenadas xey. Puede ver una relación y determinar su dominio y rango. Supongamos que está trabajando con la siguiente relación: (2, -3), (4, 6), (3, -1), (6, 6), (2, 3).[1]
1 Escriba la relación. Una relación es un conjunto de pares ordenados con coordenadas xey. Puede ver una relación y determinar su dominio y rango. Supongamos que está trabajando con la siguiente relación: (2, -3), (4, 6), (3, -1), (6, 6), (2, 3).[1]  2 Enumera las coordenadas y de la relación. Para encontrar el rango de la relación, simplemente anote todas las coordenadas y de cada par ordenado: -3, 6, -1, 6, 3.[2]
2 Enumera las coordenadas y de la relación. Para encontrar el rango de la relación, simplemente anote todas las coordenadas y de cada par ordenado: -3, 6, -1, 6, 3.[2]  3 Elimine las coordenadas duplicadas para que solo tenga una de cada coordenada y. Notarás que has enlistado "6" dos veces. Sácalo para que te quede -3, -1, 6, 3.[3]
3 Elimine las coordenadas duplicadas para que solo tenga una de cada coordenada y. Notarás que has enlistado "6" dos veces. Sácalo para que te quede -3, -1, 6, 3.[3] 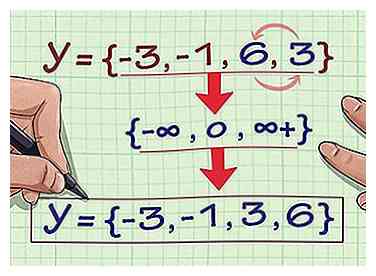 4 Escribe el rango de la relación en orden ascendente. Ahora, reordene los números en el conjunto para que se mueva del más pequeño al más grande, y usted tiene su rango. El rango de la relación (2, -3), (4, 6), (3, -1), (6, 6), (2, 3) es -3, -1, 3, 6 . Ya has terminado.[4]
4 Escribe el rango de la relación en orden ascendente. Ahora, reordene los números en el conjunto para que se mueva del más pequeño al más grande, y usted tiene su rango. El rango de la relación (2, -3), (4, 6), (3, -1), (6, 6), (2, 3) es -3, -1, 3, 6 . Ya has terminado.[4]  5 Asegúrate de que la relación es Una función. Para que una relación sea una función, cada vez que ingresas un número de una coordenada x, la coordenada y tiene que ser la misma. Por ejemplo, la relación (2, 3) (2, 4) (6, 9) es no una función, porque cuando pones 2 como una x la primera vez, obtienes un 3, pero la segunda vez que pones un 2, obtienes un cuatro. Para que una relación sea una función, si pones la misma entrada, siempre deberías obtener el mismo resultado. Si coloca un -7, debe obtener la misma coordenada y (cualquiera que sea) cada vez.[5]
5 Asegúrate de que la relación es Una función. Para que una relación sea una función, cada vez que ingresas un número de una coordenada x, la coordenada y tiene que ser la misma. Por ejemplo, la relación (2, 3) (2, 4) (6, 9) es no una función, porque cuando pones 2 como una x la primera vez, obtienes un 3, pero la segunda vez que pones un 2, obtienes un cuatro. Para que una relación sea una función, si pones la misma entrada, siempre deberías obtener el mismo resultado. Si coloca un -7, debe obtener la misma coordenada y (cualquiera que sea) cada vez.[5]  1 Lee el problema Digamos que estás trabajando con el siguiente problema: "Becky está vendiendo boletos para el concurso de talentos de su escuela por 5 dólares cada uno. La cantidad de dinero que recauda es una función de la cantidad de boletos que vende. ¿Cuál es el rango de la función?"
1 Lee el problema Digamos que estás trabajando con el siguiente problema: "Becky está vendiendo boletos para el concurso de talentos de su escuela por 5 dólares cada uno. La cantidad de dinero que recauda es una función de la cantidad de boletos que vende. ¿Cuál es el rango de la función?"  2 Escribe el problema como una función. En este caso, METRO representa la cantidad de dinero que recauda, y t representa la cantidad de boletos que ella vende.Sin embargo, dado que cada boleto costará 5 dólares, tendrá que multiplicar la cantidad de boletos vendidos por 5 para encontrar la cantidad de dinero. Por lo tanto, la función se puede escribir como M (t) = 5t.
2 Escribe el problema como una función. En este caso, METRO representa la cantidad de dinero que recauda, y t representa la cantidad de boletos que ella vende.Sin embargo, dado que cada boleto costará 5 dólares, tendrá que multiplicar la cantidad de boletos vendidos por 5 para encontrar la cantidad de dinero. Por lo tanto, la función se puede escribir como M (t) = 5t.  3 Determine el dominio Para determinar el rango, primero debe encontrar el dominio. El dominio es todos los valores posibles de t que funcionan en la ecuación. En este caso, Becky puede vender 0 o más boletos: no puede vender boletos negativos. Dado que no conocemos el número de escaños en el auditorio de su escuela, podemos suponer que teóricamente puede vender un número infinito de boletos. Y ella solo puede vender boletos enteros; ella no puede vender 1/2 de un boleto, por ejemplo. Por lo tanto, el dominio de la función es t = cualquier entero no negativo.
3 Determine el dominio Para determinar el rango, primero debe encontrar el dominio. El dominio es todos los valores posibles de t que funcionan en la ecuación. En este caso, Becky puede vender 0 o más boletos: no puede vender boletos negativos. Dado que no conocemos el número de escaños en el auditorio de su escuela, podemos suponer que teóricamente puede vender un número infinito de boletos. Y ella solo puede vender boletos enteros; ella no puede vender 1/2 de un boleto, por ejemplo. Por lo tanto, el dominio de la función es t = cualquier entero no negativo.  4 Determine el rango. El rango es la cantidad de dinero posible que Becky puede obtener de su venta. Tienes que trabajar con el dominio para encontrar el rango. Si sabe que el dominio es un entero no negativo y que la fórmula es M (t) = 5t, entonces sabes que puedes conectar cualquier entero no negativo en esta función para obtener la salida o el rango. Por ejemplo, si vende 5 boletos, entonces M (5) = 5 x 5 o 25 dólares. Si ella vende 100, entonces M (100) = 5 x 100 o 500 dólares. Por lo tanto, el rango de la función es cualquier entero no negativo que es un múltiplo de cinco.
4 Determine el rango. El rango es la cantidad de dinero posible que Becky puede obtener de su venta. Tienes que trabajar con el dominio para encontrar el rango. Si sabe que el dominio es un entero no negativo y que la fórmula es M (t) = 5t, entonces sabes que puedes conectar cualquier entero no negativo en esta función para obtener la salida o el rango. Por ejemplo, si vende 5 boletos, entonces M (5) = 5 x 5 o 25 dólares. Si ella vende 100, entonces M (100) = 5 x 100 o 500 dólares. Por lo tanto, el rango de la función es cualquier entero no negativo que es un múltiplo de cinco.