El dominio de una función es el conjunto de números que pueden ir a una función dada. En otras palabras, es el conjunto de valores-x los que puedes poner en cualquier ecuación dada. El conjunto de posibles valores y se llama rango. Si desea saber cómo encontrar el dominio de una función en una variedad de situaciones, solo siga estos pasos.
Método uno de seis:
Aprendiendo lo Básico
-
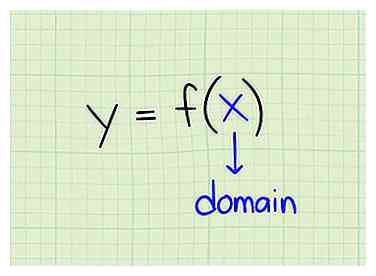 1 Aprende la definición del dominio. El dominio se define como el conjunto de valores de entrada para el cual la función produce un valor de salida. En otras palabras, el dominio es el conjunto completo de valores x que se pueden conectar a una función para producir un valor y.
1 Aprende la definición del dominio. El dominio se define como el conjunto de valores de entrada para el cual la función produce un valor de salida. En otras palabras, el dominio es el conjunto completo de valores x que se pueden conectar a una función para producir un valor y. -
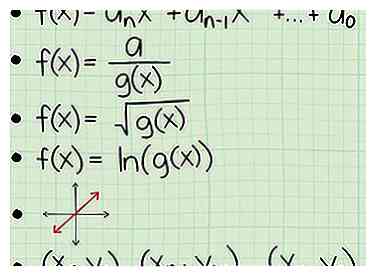 2 Aprenda cómo encontrar el dominio de una variedad de funciones. El tipo de función determinará el mejor método para encontrar un dominio. Estos son los conceptos básicos que necesita saber sobre cada tipo de función, que se explicarán en la siguiente sección:
2 Aprenda cómo encontrar el dominio de una variedad de funciones. El tipo de función determinará el mejor método para encontrar un dominio. Estos son los conceptos básicos que necesita saber sobre cada tipo de función, que se explicarán en la siguiente sección: - Una función polinomial sin radicales o variables en el denominador. Para este tipo de función, el dominio son todos números reales.
- Una función con una fracción con una variable en el denominador. Para encontrar el dominio de este tipo de función, establezca el fondo igual a cero y excluya el valor de x que encuentre cuando resuelva la ecuación.
- Una función con una variable dentro de un signo radical. Para encontrar el dominio de este tipo de función, simplemente establezca los términos dentro del signo radical a> 0 y resuelva para encontrar los valores que funcionarían para x.
- Una función que utiliza el registro natural (ln). Simplemente establece los términos entre paréntesis en> 0 y resuelve.
- Un gráfico. Mira el gráfico para ver qué valores funcionan para x.
- Una relación. Esta será una lista de coordenadas xey. Su dominio simplemente será una lista de x coordenadas.
-
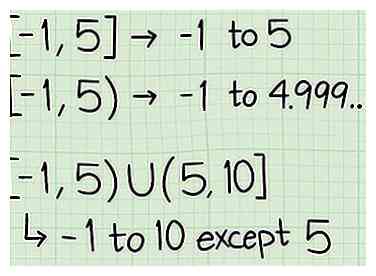 3 Indique correctamente el dominio. La notación adecuada para el dominio es fácil de aprender, pero es importante que la escriba correctamente para expresar la respuesta correcta y obtener puntos completos en las tareas y exámenes. Aquí hay algunas cosas que necesita saber sobre cómo escribir el dominio de una función:
3 Indique correctamente el dominio. La notación adecuada para el dominio es fácil de aprender, pero es importante que la escriba correctamente para expresar la respuesta correcta y obtener puntos completos en las tareas y exámenes. Aquí hay algunas cosas que necesita saber sobre cómo escribir el dominio de una función: - El formato para expresar el dominio es un corchete / paréntesis abierto, seguido de los 2 puntos finales del dominio separados por una coma, seguido de un corchete / paréntesis cerrado.
- Por ejemplo, [-1,5). Esto significa que el dominio va de -1 a 5.
- Use corchetes como [ y ] para indicar que un número está incluido en el dominio.
- Entonces en el ejemplo, [-1,5), el dominio incluye -1.
- Use paréntesis como ( y ) para indicar que un número no está incluido en el dominio.
- Entonces en el ejemplo, [-1,5), 5 no está incluido en el dominio. El dominio se detiene arbitrariamente menos de 5, es decir, 4.999 ...
- Use "U" (que significa "unión") para conectar partes del dominio que están separadas por un espacio. '
- Por ejemplo, [-1,5] U (5,10). Esto significa que el dominio va de -1 a 10, inclusive, pero que hay un espacio en el dominio en 5. Esto podría ser el resultado de, para ejemplo, una función con "x - 5" en el denominador.
- Puede usar tantos símbolos "U" como sea necesario si el dominio tiene múltiples espacios.
- Usa infinito y signos negativos de infinito para expresar que el dominio continúa infinitamente en cualquier dirección.
- Siempre use (), no [], con símbolos de infinito.
- El formato para expresar el dominio es un corchete / paréntesis abierto, seguido de los 2 puntos finales del dominio separados por una coma, seguido de un corchete / paréntesis cerrado.
Método dos de seis:
Encontrar el dominio de una función con una fracción
-
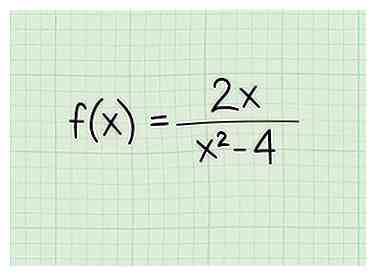 1 Escribe el problema Digamos que estás trabajando con el siguiente problema:
1 Escribe el problema Digamos que estás trabajando con el siguiente problema: - f (x) = 2x / (x2 - 4)
-
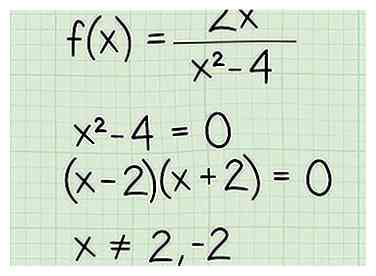 2 Establezca el denominador igual a cero para las fracciones con una variable en el denominador. Al encontrar el dominio de una función fraccionaria, debe excluir todos los valores x que hacen que el denominador sea igual a cero, porque nunca se puede dividir por cero. Entonces, escribe el denominador como una ecuación y configúralo como 0. Así es como lo haces:
2 Establezca el denominador igual a cero para las fracciones con una variable en el denominador. Al encontrar el dominio de una función fraccionaria, debe excluir todos los valores x que hacen que el denominador sea igual a cero, porque nunca se puede dividir por cero. Entonces, escribe el denominador como una ecuación y configúralo como 0. Así es como lo haces: - f (x) = 2x / (x2 - 4)
- X2 - 4 = 0
- (x - 2) (x + 2) = 0
- x ≠ (2, - 2)
-
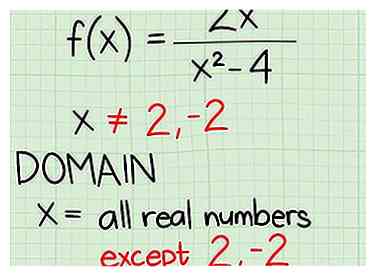 3 Indique el dominio. Así es como lo haces:
3 Indique el dominio. Así es como lo haces: - x = todos los números reales excepto 2 y -2
Método tres de seis:
Encontrar el dominio de una función con una raíz cuadrada
-
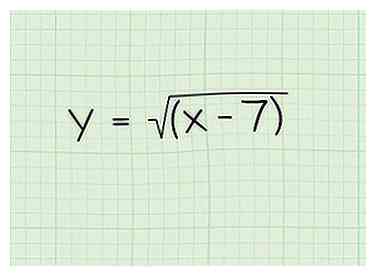 1 Escribe el problema Supongamos que está trabajando con el siguiente problema: Y = √ (x-7)
1 Escribe el problema Supongamos que está trabajando con el siguiente problema: Y = √ (x-7) -
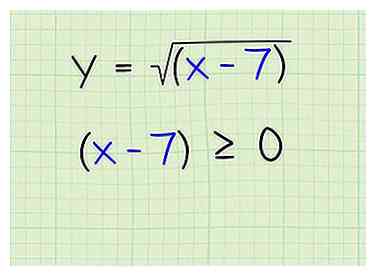 2 Establezca los términos dentro del radicando para que sean mayores o iguales a 0. No puede tomar la raíz cuadrada de un número negativo, aunque puede tomar la raíz cuadrada de 0. Entonces, establezca los términos dentro del radicando para que sean mayores o iguales a 0. Note que esto aplica no solo a las raíces cuadradas, sino a todas las raíces con número par. Sin embargo, no se aplica a las raíces con números impares, porque está perfectamente bien tener negativos bajo raíces raras. Así es cómo:
2 Establezca los términos dentro del radicando para que sean mayores o iguales a 0. No puede tomar la raíz cuadrada de un número negativo, aunque puede tomar la raíz cuadrada de 0. Entonces, establezca los términos dentro del radicando para que sean mayores o iguales a 0. Note que esto aplica no solo a las raíces cuadradas, sino a todas las raíces con número par. Sin embargo, no se aplica a las raíces con números impares, porque está perfectamente bien tener negativos bajo raíces raras. Así es cómo: - x-7 ≧ 0
-
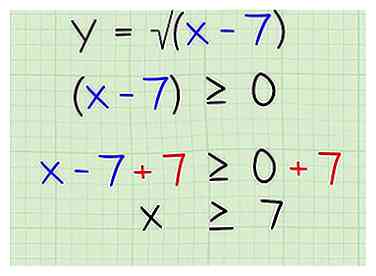 3 Aislar la variable. Ahora, para aislar x en el lado izquierdo de la ecuación, solo agrega 7 a ambos lados, por lo que te queda lo siguiente:
3 Aislar la variable. Ahora, para aislar x en el lado izquierdo de la ecuación, solo agrega 7 a ambos lados, por lo que te queda lo siguiente: - x ≧ 7
-
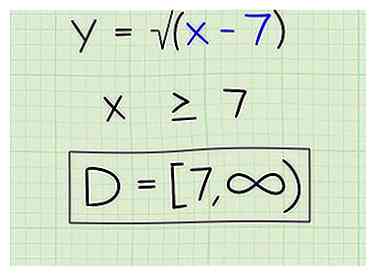 4 Indique el dominio correctamente. Así es como lo escribirías:
4 Indique el dominio correctamente. Así es como lo escribirías: - D = [7, ∞)
-
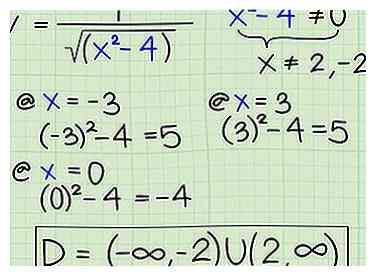 5 Encuentre el dominio de una función con una raíz cuadrada cuando hay múltiples soluciones. Supongamos que está trabajando con la siguiente función: Y = 1 / √ (̅x2 -4). Cuando factorizas el denominador y lo estableces igual a cero, obtendrás x ≠ (2, - 2). Aquí es a donde vas desde allí:
5 Encuentre el dominio de una función con una raíz cuadrada cuando hay múltiples soluciones. Supongamos que está trabajando con la siguiente función: Y = 1 / √ (̅x2 -4). Cuando factorizas el denominador y lo estableces igual a cero, obtendrás x ≠ (2, - 2). Aquí es a donde vas desde allí: - Ahora, verifique el área debajo de -2 (taponando -3, por ejemplo), para ver si los números debajo de -2 se pueden conectar al denominador para dar un número mayor que 0. Lo hacen.
- (-3)2 - 4 = 5
- Ahora, verifique el área entre -2 y 2. Seleccione 0, por ejemplo.
- 02 - 4 = -4, entonces sabes que los números entre -2 y 2 no funcionan.
- Ahora pruebe un número por encima de 2, como +3.
- 32 - 4 = 5, por lo que los números mayores de 2 sí funcionan.
- Escribe el dominio cuando hayas terminado. Así es como escribirías el dominio:
- D = (-∞, -2) U (2, ∞)
- Ahora, verifique el área debajo de -2 (taponando -3, por ejemplo), para ver si los números debajo de -2 se pueden conectar al denominador para dar un número mayor que 0. Lo hacen.
Método cuatro de seis:
Encontrar el dominio de una función usando un registro natural
-
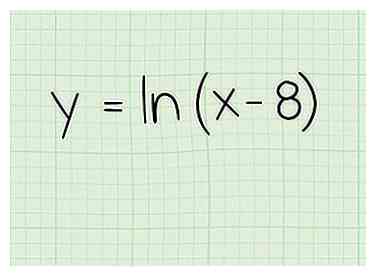 1 Escribe el problema Digamos que estás trabajando con este:
1 Escribe el problema Digamos que estás trabajando con este: - f (x) = ln (x-8)
-
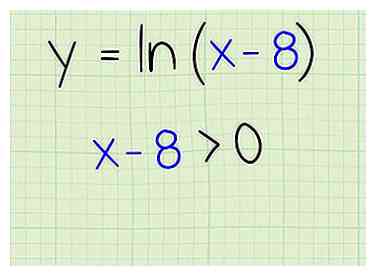 2 Establezca los términos entre paréntesis en mayor que cero. El registro natural tiene que ser un número positivo, por lo tanto, establezca los términos entre paréntesis en mayor que cero para que así sea. Esto es lo que haces:
2 Establezca los términos entre paréntesis en mayor que cero. El registro natural tiene que ser un número positivo, por lo tanto, establezca los términos entre paréntesis en mayor que cero para que así sea. Esto es lo que haces: - x - 8> 0
-
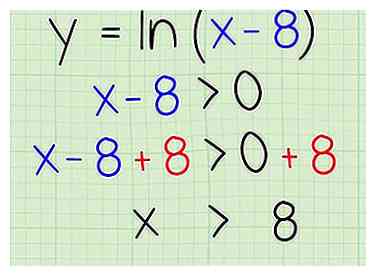 3 Resolver. Simplemente aísle la variable x agregando 8 a ambos lados. Así es cómo:
3 Resolver. Simplemente aísle la variable x agregando 8 a ambos lados. Así es cómo: - x - 8 + 8> 0 + 8
- x> 8
-
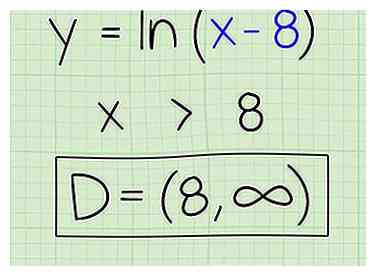 4 Indique el dominio. Demuestre que el dominio para esta ecuación es igual a todos los números mayores que 8 hasta el infinito. Así es cómo:
4 Indique el dominio. Demuestre que el dominio para esta ecuación es igual a todos los números mayores que 8 hasta el infinito. Así es cómo: - D = (8, ∞)
Método cinco de seis:
Encontrar el dominio de una función usando un gráfico
-
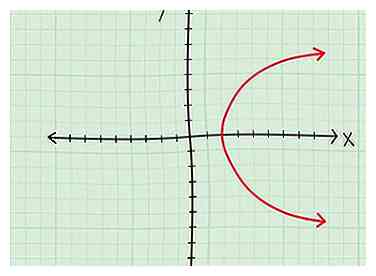 1 Mira el gráfico.
1 Mira el gráfico. -
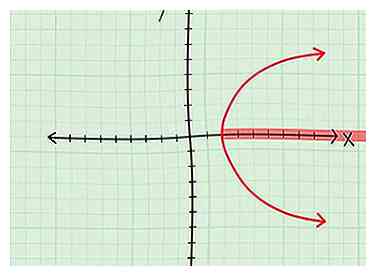 2 Echa un vistazo a los valores de x que se incluyen en el gráfico. Esto puede ser más fácil decirlo que hacerlo, pero aquí hay algunos consejos:
2 Echa un vistazo a los valores de x que se incluyen en el gráfico. Esto puede ser más fácil decirlo que hacerlo, pero aquí hay algunos consejos: - Una linea Si ve una línea en el gráfico que se extiende hasta el infinito, entonces todas versiones de x se cubrirán con el tiempo, por lo que el dominio es igual a todos los números reales.
- Una parábola normal. Si ve una parábola que se enfrenta hacia arriba o hacia abajo, entonces sí, el dominio será todos los números reales, porque todos los números en el eje x eventualmente serán cubiertos.
- Una parábola lateral. Ahora, si tienes una parábola con un vértice en (4,0) que se extiende infinitamente a la derecha, entonces tu dominio es D = [4, ∞]
-
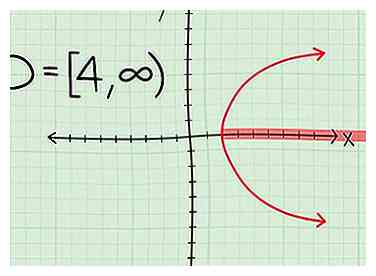 3 Indique el dominio. Simplemente indique el dominio según el tipo de gráfico con el que está trabajando. Si no está seguro y conoce la ecuación de la línea, vuelva a enchufar las coordenadas x en la función para verificar.
3 Indique el dominio. Simplemente indique el dominio según el tipo de gráfico con el que está trabajando. Si no está seguro y conoce la ecuación de la línea, vuelva a enchufar las coordenadas x en la función para verificar.
Método Seis de seis:
Encontrar el dominio de una función usando una relación
-
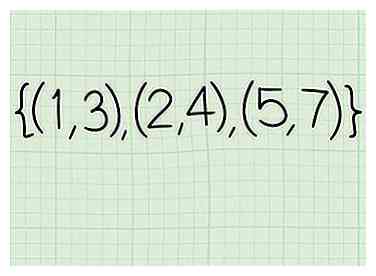 1 Escriba la relación. Una relación es solo un conjunto de coordenadas xey. Supongamos que está trabajando con las siguientes coordenadas: (1, 3), (2, 4), (5, 7)
1 Escriba la relación. Una relación es solo un conjunto de coordenadas xey. Supongamos que está trabajando con las siguientes coordenadas: (1, 3), (2, 4), (5, 7) -
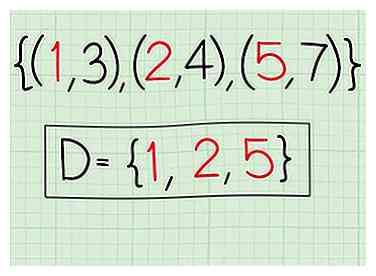 2 Escriba las coordenadas x. Ellos son: 1, 2, 5.
2 Escriba las coordenadas x. Ellos son: 1, 2, 5. -
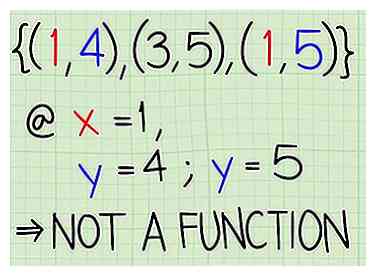 3 Indique el dominio. D = 1, 2, 5
3 Indique el dominio. D = 1, 2, 5 - 4 Asegúrate de que la relación sea una función. Para que una relación sea una función, cada vez que pones una coordenada x numérica, deberías obtener la misma coordenada y. Por lo tanto, si coloca 3 para x, siempre debe obtener 6 para y, y así sucesivamente. La siguiente relación es no una función porque obtienes dos valores diferentes de "y" para cada valor de "x": (1, 4), (3, 5), (1, 5).[1]
 Minotauromaquia
Minotauromaquia
 1 Aprende la definición del dominio. El dominio se define como el conjunto de valores de entrada para el cual la función produce un valor de salida. En otras palabras, el dominio es el conjunto completo de valores x que se pueden conectar a una función para producir un valor y.
1 Aprende la definición del dominio. El dominio se define como el conjunto de valores de entrada para el cual la función produce un valor de salida. En otras palabras, el dominio es el conjunto completo de valores x que se pueden conectar a una función para producir un valor y. 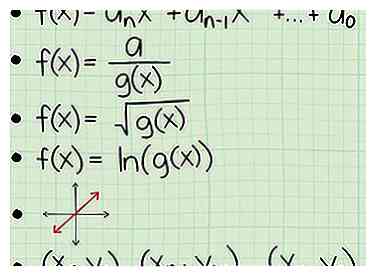 2 Aprenda cómo encontrar el dominio de una variedad de funciones. El tipo de función determinará el mejor método para encontrar un dominio. Estos son los conceptos básicos que necesita saber sobre cada tipo de función, que se explicarán en la siguiente sección:
2 Aprenda cómo encontrar el dominio de una variedad de funciones. El tipo de función determinará el mejor método para encontrar un dominio. Estos son los conceptos básicos que necesita saber sobre cada tipo de función, que se explicarán en la siguiente sección: 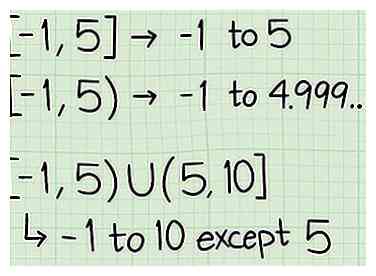 3 Indique correctamente el dominio. La notación adecuada para el dominio es fácil de aprender, pero es importante que la escriba correctamente para expresar la respuesta correcta y obtener puntos completos en las tareas y exámenes. Aquí hay algunas cosas que necesita saber sobre cómo escribir el dominio de una función:
3 Indique correctamente el dominio. La notación adecuada para el dominio es fácil de aprender, pero es importante que la escriba correctamente para expresar la respuesta correcta y obtener puntos completos en las tareas y exámenes. Aquí hay algunas cosas que necesita saber sobre cómo escribir el dominio de una función: 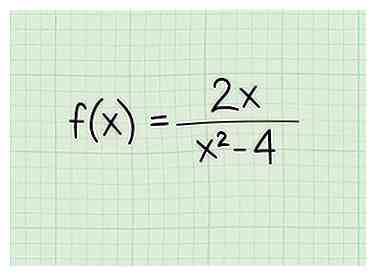 1 Escribe el problema Digamos que estás trabajando con el siguiente problema:
1 Escribe el problema Digamos que estás trabajando con el siguiente problema: 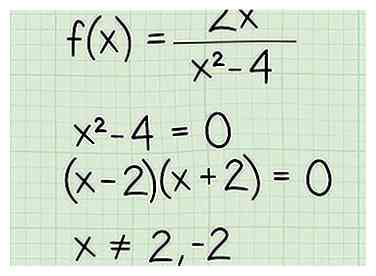 2 Establezca el denominador igual a cero para las fracciones con una variable en el denominador. Al encontrar el dominio de una función fraccionaria, debe excluir todos los valores x que hacen que el denominador sea igual a cero, porque nunca se puede dividir por cero. Entonces, escribe el denominador como una ecuación y configúralo como 0. Así es como lo haces:
2 Establezca el denominador igual a cero para las fracciones con una variable en el denominador. Al encontrar el dominio de una función fraccionaria, debe excluir todos los valores x que hacen que el denominador sea igual a cero, porque nunca se puede dividir por cero. Entonces, escribe el denominador como una ecuación y configúralo como 0. Así es como lo haces: 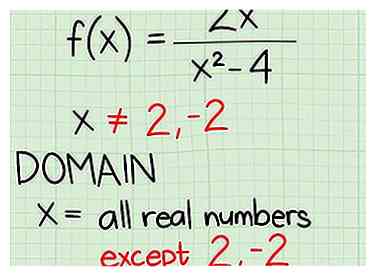 3 Indique el dominio. Así es como lo haces:
3 Indique el dominio. Así es como lo haces: 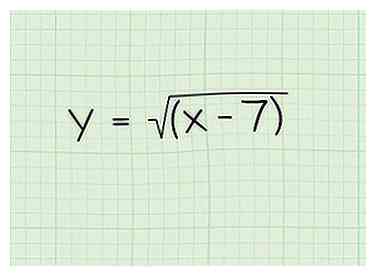 1 Escribe el problema Supongamos que está trabajando con el siguiente problema: Y = √ (x-7)
1 Escribe el problema Supongamos que está trabajando con el siguiente problema: Y = √ (x-7) 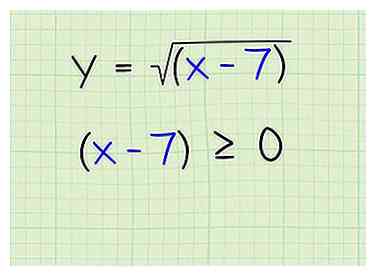 2 Establezca los términos dentro del radicando para que sean mayores o iguales a 0. No puede tomar la raíz cuadrada de un número negativo, aunque puede tomar la raíz cuadrada de 0. Entonces, establezca los términos dentro del radicando para que sean mayores o iguales a 0. Note que esto aplica no solo a las raíces cuadradas, sino a todas las raíces con número par. Sin embargo, no se aplica a las raíces con números impares, porque está perfectamente bien tener negativos bajo raíces raras. Así es cómo:
2 Establezca los términos dentro del radicando para que sean mayores o iguales a 0. No puede tomar la raíz cuadrada de un número negativo, aunque puede tomar la raíz cuadrada de 0. Entonces, establezca los términos dentro del radicando para que sean mayores o iguales a 0. Note que esto aplica no solo a las raíces cuadradas, sino a todas las raíces con número par. Sin embargo, no se aplica a las raíces con números impares, porque está perfectamente bien tener negativos bajo raíces raras. Así es cómo: 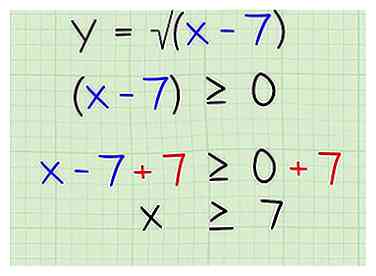 3 Aislar la variable. Ahora, para aislar x en el lado izquierdo de la ecuación, solo agrega 7 a ambos lados, por lo que te queda lo siguiente:
3 Aislar la variable. Ahora, para aislar x en el lado izquierdo de la ecuación, solo agrega 7 a ambos lados, por lo que te queda lo siguiente: 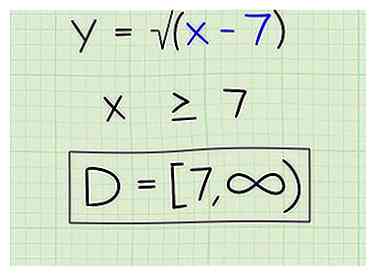 4 Indique el dominio correctamente. Así es como lo escribirías:
4 Indique el dominio correctamente. Así es como lo escribirías: 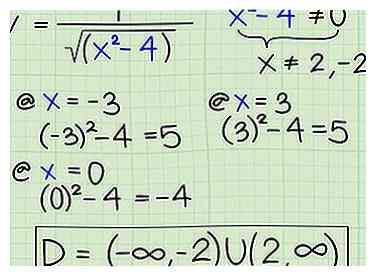 5 Encuentre el dominio de una función con una raíz cuadrada cuando hay múltiples soluciones. Supongamos que está trabajando con la siguiente función: Y = 1 / √ (̅x2 -4). Cuando factorizas el denominador y lo estableces igual a cero, obtendrás x ≠ (2, - 2). Aquí es a donde vas desde allí:
5 Encuentre el dominio de una función con una raíz cuadrada cuando hay múltiples soluciones. Supongamos que está trabajando con la siguiente función: Y = 1 / √ (̅x2 -4). Cuando factorizas el denominador y lo estableces igual a cero, obtendrás x ≠ (2, - 2). Aquí es a donde vas desde allí: 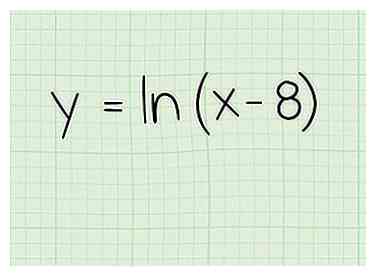 1 Escribe el problema Digamos que estás trabajando con este:
1 Escribe el problema Digamos que estás trabajando con este: 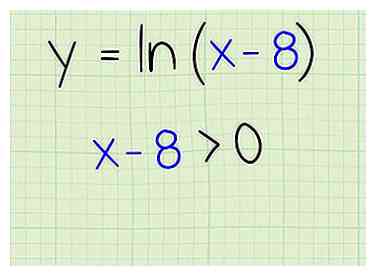 2 Establezca los términos entre paréntesis en mayor que cero. El registro natural tiene que ser un número positivo, por lo tanto, establezca los términos entre paréntesis en mayor que cero para que así sea. Esto es lo que haces:
2 Establezca los términos entre paréntesis en mayor que cero. El registro natural tiene que ser un número positivo, por lo tanto, establezca los términos entre paréntesis en mayor que cero para que así sea. Esto es lo que haces: 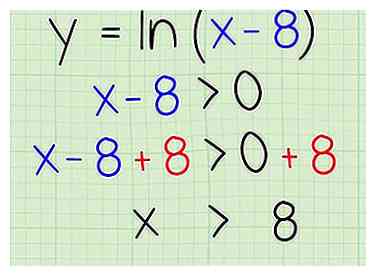 3 Resolver. Simplemente aísle la variable x agregando 8 a ambos lados. Así es cómo:
3 Resolver. Simplemente aísle la variable x agregando 8 a ambos lados. Así es cómo: 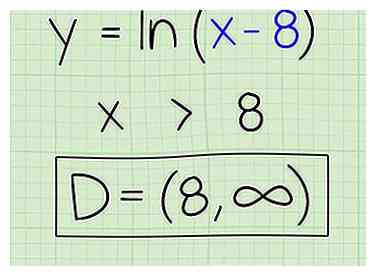 4 Indique el dominio. Demuestre que el dominio para esta ecuación es igual a todos los números mayores que 8 hasta el infinito. Así es cómo:
4 Indique el dominio. Demuestre que el dominio para esta ecuación es igual a todos los números mayores que 8 hasta el infinito. Así es cómo:  1 Mira el gráfico.
1 Mira el gráfico.  2 Echa un vistazo a los valores de x que se incluyen en el gráfico. Esto puede ser más fácil decirlo que hacerlo, pero aquí hay algunos consejos:
2 Echa un vistazo a los valores de x que se incluyen en el gráfico. Esto puede ser más fácil decirlo que hacerlo, pero aquí hay algunos consejos:  3 Indique el dominio. Simplemente indique el dominio según el tipo de gráfico con el que está trabajando. Si no está seguro y conoce la ecuación de la línea, vuelva a enchufar las coordenadas x en la función para verificar.
3 Indique el dominio. Simplemente indique el dominio según el tipo de gráfico con el que está trabajando. Si no está seguro y conoce la ecuación de la línea, vuelva a enchufar las coordenadas x en la función para verificar. 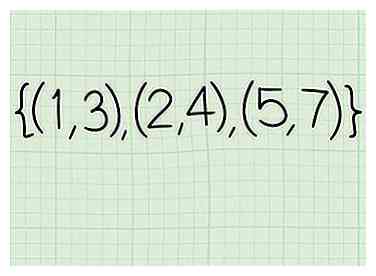 1 Escriba la relación. Una relación es solo un conjunto de coordenadas xey. Supongamos que está trabajando con las siguientes coordenadas: (1, 3), (2, 4), (5, 7)
1 Escriba la relación. Una relación es solo un conjunto de coordenadas xey. Supongamos que está trabajando con las siguientes coordenadas: (1, 3), (2, 4), (5, 7) 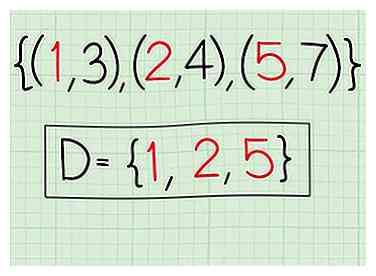 2 Escriba las coordenadas x. Ellos son: 1, 2, 5.
2 Escriba las coordenadas x. Ellos son: 1, 2, 5. 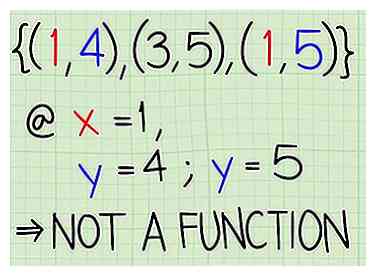 3 Indique el dominio. D = 1, 2, 5
3 Indique el dominio. D = 1, 2, 5