A diferencia de una línea recta, la pendiente de una curva cambia constantemente a medida que avanzas a lo largo del gráfico. El cálculo presenta a los estudiantes la idea de que cada punto de este gráfico se podría describir con una pendiente o una "tasa de cambio instantánea". La línea tangente es una línea recta con esa pendiente, pasando por ese punto exacto en el gráfico. Para encontrar la ecuación para la tangente, necesitarás saber cómo tomar la derivada de la ecuación original.
Método uno de dos:
Encontrar la ecuación de una línea tangente
-
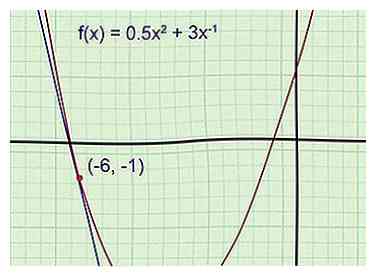 1 Dibuje la función y la línea tangente (recomendado). Un gráfico facilita seguir el problema y verificar si la respuesta tiene sentido. Dibuje la función en un papel cuadriculado, usando una calculadora gráfica como referencia si es necesario. Dibuja la línea tangente que pasa por el punto dado. (Recuerde, la línea tangente recorre ese punto y tiene la misma pendiente que el gráfico en ese punto).
1 Dibuje la función y la línea tangente (recomendado). Un gráfico facilita seguir el problema y verificar si la respuesta tiene sentido. Dibuje la función en un papel cuadriculado, usando una calculadora gráfica como referencia si es necesario. Dibuja la línea tangente que pasa por el punto dado. (Recuerde, la línea tangente recorre ese punto y tiene la misma pendiente que el gráfico en ese punto). - Ejemplo 1: Dibuja el gráfico de la parábola . Dibuja la tangente pasando por el punto (-6, -1).
Aún no conoce la ecuación de la tangente, pero ya puede decir que su pendiente es negativa, y que su intersección en y es negativa (muy por debajo del vértice de la parábola con el valor y de -5.5). Si su respuesta final no coincide con estos detalles, sabrá verificar su trabajo para detectar errores.
- Ejemplo 1: Dibuja el gráfico de la parábola . Dibuja la tangente pasando por el punto (-6, -1).
-
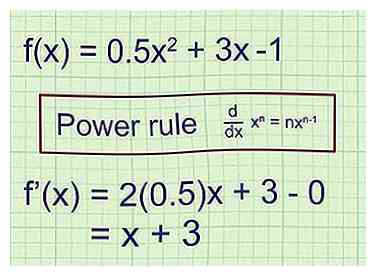 2 Tome la primera derivada para encontrar la ecuación para el cuesta abajo de la línea tangente. Para la función f (x), la primera derivada f '(x) representa la ecuación para la pendiente de la recta tangente en cualquier punto de f (x). Hay muchas formas de tomar derivados. Aquí hay un ejemplo simple usando la regla de poder:[1]
2 Tome la primera derivada para encontrar la ecuación para el cuesta abajo de la línea tangente. Para la función f (x), la primera derivada f '(x) representa la ecuación para la pendiente de la recta tangente en cualquier punto de f (x). Hay muchas formas de tomar derivados. Aquí hay un ejemplo simple usando la regla de poder:[1] - Ejemplo 1 (cont.): El gráfico está descrito por la función .
Recuerde la regla de poder al tomar derivados: .
La primera derivada de la función = f '(x) = (2) (0.5) x + 3 - 0.
f '(x) = x + 3. Inserte cualquier valor a para x en esta ecuación, y el resultado será la pendiente de la recta tangente a f (x) en el punto donde x = a.
- Ejemplo 1 (cont.): El gráfico está descrito por la función .
-
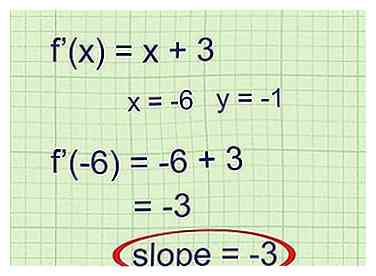 3 Ingrese el valor x del punto que está investigando. Lee el problema para descubrir las coordenadas del punto para el que estás buscando la línea tangente. Ingrese la coordenada x de este punto en f '(x). La salida es la pendiente de la línea tangente en este punto.
3 Ingrese el valor x del punto que está investigando. Lee el problema para descubrir las coordenadas del punto para el que estás buscando la línea tangente. Ingrese la coordenada x de este punto en f '(x). La salida es la pendiente de la línea tangente en este punto. - Ejemplo 1 (cont.): El punto mencionado en el problema es (-6, -1). Use la coordenada x -6 como la entrada para f '(x):
f '(- 6) = -6 + 3 = -3
La pendiente de la línea tangente es -3.
- Ejemplo 1 (cont.): El punto mencionado en el problema es (-6, -1). Use la coordenada x -6 como la entrada para f '(x):
-
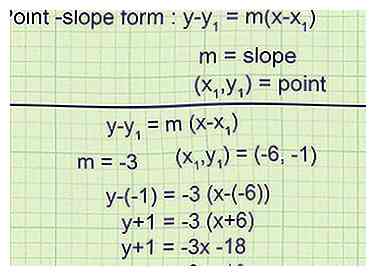 4 Escribe la ecuación de la recta tangente en forma de punto y pendiente. La forma de pendiente de punto de una ecuación lineal es , dónde metro es la pendiente y es un punto en la línea.[2] Ahora tiene toda la información que necesita para escribir la ecuación de la recta tangente en esta forma.
4 Escribe la ecuación de la recta tangente en forma de punto y pendiente. La forma de pendiente de punto de una ecuación lineal es , dónde metro es la pendiente y es un punto en la línea.[2] Ahora tiene toda la información que necesita para escribir la ecuación de la recta tangente en esta forma. - Ejemplo 1 (cont.):
La pendiente de la línea es -3, entonces
La línea tangente pasa por (-6, -1), por lo que la ecuación final es
Simplificar a
- Ejemplo 1 (cont.):
-
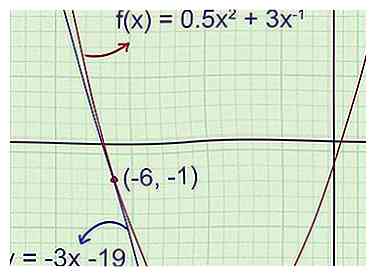 5 Confirma la ecuación en tu gráfica. Si tiene una calculadora gráfica, grafique la función original y la línea tangente para verificar que tiene la respuesta correcta. Si trabaja en papel, consulte el gráfico anterior para asegurarse de que no haya errores evidentes en su respuesta.
5 Confirma la ecuación en tu gráfica. Si tiene una calculadora gráfica, grafique la función original y la línea tangente para verificar que tiene la respuesta correcta. Si trabaja en papel, consulte el gráfico anterior para asegurarse de que no haya errores evidentes en su respuesta. - Ejemplo 1 (cont.): El boceto inicial mostró que la pendiente de la línea tangente era negativa, y la intersección con el eje y estaba muy por debajo de -5.5. La ecuación de la recta tangente que encontramos es y = -3x - 19 en la forma pendiente-intersección, lo que significa que -3 es la pendiente y -19 es la intersección en y. Ambos atributos coinciden con las predicciones iniciales.
-
 6 Intenta un problema más difícil. Aquí hay un repaso de todo el proceso nuevamente. Esta vez, el objetivo es encontrar la línea tangente a en x = 2:
6 Intenta un problema más difícil. Aquí hay un repaso de todo el proceso nuevamente. Esta vez, el objetivo es encontrar la línea tangente a en x = 2: - Usando la regla de poder, la primera derivada . Esta función nos dirá la pendiente de la tangente.
- Como x = 2, encuentra . Esta es la pendiente en x = 2.
- Tenga en cuenta que esta vez no tenemos un punto, solo una coordenada x. Para encontrar la coordenada y, conecte x = 2 en la función inicial: . El punto es (2,27).
- Escribe la ecuación de la recta tangente en forma de punto y pendiente:
Si es necesario, simplifique a y = 25x - 23.
Método dos de dos:
Resolviendo problemas relacionados
-
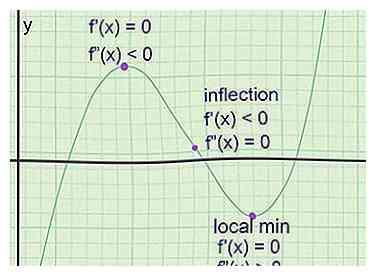 1 Encuentra los puntos extremos en un gráfico. Estos son puntos donde el gráfico alcanza un máximo local (un punto más alto que los puntos de cada lado) o un mínimo local (más bajo que los puntos de cada lado). La línea tangente siempre tiene una pendiente de 0 en estos puntos (una línea horizontal), pero una pendiente cero sola no garantiza un punto extremo. He aquí cómo encontrarlos:[3]
1 Encuentra los puntos extremos en un gráfico. Estos son puntos donde el gráfico alcanza un máximo local (un punto más alto que los puntos de cada lado) o un mínimo local (más bajo que los puntos de cada lado). La línea tangente siempre tiene una pendiente de 0 en estos puntos (una línea horizontal), pero una pendiente cero sola no garantiza un punto extremo. He aquí cómo encontrarlos:[3] - Tome la primera derivada de la función para obtener f '(x), la ecuación para la pendiente de la tangente.
- Resuelve para f '(x) = 0 para encontrar posible puntos extremos
- Tome la segunda derivada para obtener f "(x), la ecuación que le dice qué tan rápido está cambiando la pendiente de la tangente.
- Para cada posible punto extremo, conecte la coordenada x un en f "(x). Si f" (a) es positivo, hay un mínimo local en un. Si f "(a) es negativo, hay un máximo local. Si f" (a) es 0, hay un punto de inflexión, no un punto extremo.
- Si hay un máximo o mínimo en un, encuentra f (a) para obtener la coordenada y.
-
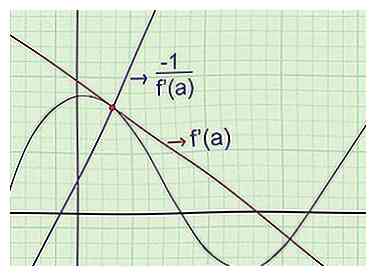 2 Encuentra la ecuación de lo normal. La "normal" a una curva en un punto particular pasa a través de ese punto, pero tiene una pendiente perpendicular a una tangente. Para encontrar la ecuación para lo normal, aproveche el hecho de que (pendiente de tangente) (pendiente de lo normal) = -1, cuando ambos pasan por el mismo punto en el gráfico.[4] En otras palabras:
2 Encuentra la ecuación de lo normal. La "normal" a una curva en un punto particular pasa a través de ese punto, pero tiene una pendiente perpendicular a una tangente. Para encontrar la ecuación para lo normal, aproveche el hecho de que (pendiente de tangente) (pendiente de lo normal) = -1, cuando ambos pasan por el mismo punto en el gráfico.[4] En otras palabras: - Encuentre f '(x), la pendiente de la línea tangente.
- Si el punto está en x = un, encuentre f '(a) para encontrar la pendiente de la tangente en ese punto.
- Calcular para encontrar la pendiente de lo normal.
- Escribe la ecuación normal en forma de punto de pendiente.
 Minotauromaquia
Minotauromaquia
 1 Dibuje la función y la línea tangente (recomendado). Un gráfico facilita seguir el problema y verificar si la respuesta tiene sentido. Dibuje la función en un papel cuadriculado, usando una calculadora gráfica como referencia si es necesario. Dibuja la línea tangente que pasa por el punto dado. (Recuerde, la línea tangente recorre ese punto y tiene la misma pendiente que el gráfico en ese punto).
1 Dibuje la función y la línea tangente (recomendado). Un gráfico facilita seguir el problema y verificar si la respuesta tiene sentido. Dibuje la función en un papel cuadriculado, usando una calculadora gráfica como referencia si es necesario. Dibuja la línea tangente que pasa por el punto dado. (Recuerde, la línea tangente recorre ese punto y tiene la misma pendiente que el gráfico en ese punto). 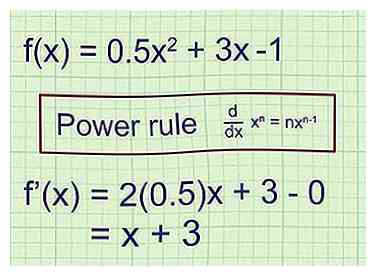 2 Tome la primera derivada para encontrar la ecuación para el cuesta abajo de la línea tangente. Para la función f (x), la primera derivada f '(x) representa la ecuación para la pendiente de la recta tangente en cualquier punto de f (x). Hay muchas formas de tomar derivados. Aquí hay un ejemplo simple usando la regla de poder:[1]
2 Tome la primera derivada para encontrar la ecuación para el cuesta abajo de la línea tangente. Para la función f (x), la primera derivada f '(x) representa la ecuación para la pendiente de la recta tangente en cualquier punto de f (x). Hay muchas formas de tomar derivados. Aquí hay un ejemplo simple usando la regla de poder:[1] 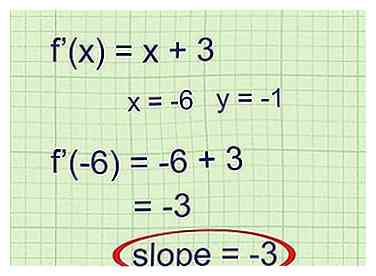 3 Ingrese el valor x del punto que está investigando. Lee el problema para descubrir las coordenadas del punto para el que estás buscando la línea tangente. Ingrese la coordenada x de este punto en f '(x). La salida es la pendiente de la línea tangente en este punto.
3 Ingrese el valor x del punto que está investigando. Lee el problema para descubrir las coordenadas del punto para el que estás buscando la línea tangente. Ingrese la coordenada x de este punto en f '(x). La salida es la pendiente de la línea tangente en este punto. 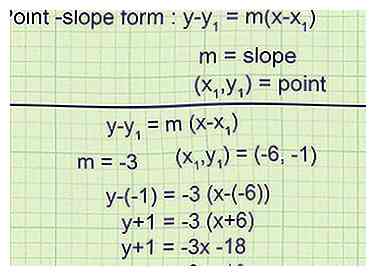 4 Escribe la ecuación de la recta tangente en forma de punto y pendiente. La forma de pendiente de punto de una ecuación lineal es
4 Escribe la ecuación de la recta tangente en forma de punto y pendiente. La forma de pendiente de punto de una ecuación lineal es  5 Confirma la ecuación en tu gráfica. Si tiene una calculadora gráfica, grafique la función original y la línea tangente para verificar que tiene la respuesta correcta. Si trabaja en papel, consulte el gráfico anterior para asegurarse de que no haya errores evidentes en su respuesta.
5 Confirma la ecuación en tu gráfica. Si tiene una calculadora gráfica, grafique la función original y la línea tangente para verificar que tiene la respuesta correcta. Si trabaja en papel, consulte el gráfico anterior para asegurarse de que no haya errores evidentes en su respuesta.  6 Intenta un problema más difícil. Aquí hay un repaso de todo el proceso nuevamente. Esta vez, el objetivo es encontrar la línea tangente a
6 Intenta un problema más difícil. Aquí hay un repaso de todo el proceso nuevamente. Esta vez, el objetivo es encontrar la línea tangente a  1 Encuentra los puntos extremos en un gráfico. Estos son puntos donde el gráfico alcanza un máximo local (un punto más alto que los puntos de cada lado) o un mínimo local (más bajo que los puntos de cada lado). La línea tangente siempre tiene una pendiente de 0 en estos puntos (una línea horizontal), pero una pendiente cero sola no garantiza un punto extremo. He aquí cómo encontrarlos:[3]
1 Encuentra los puntos extremos en un gráfico. Estos son puntos donde el gráfico alcanza un máximo local (un punto más alto que los puntos de cada lado) o un mínimo local (más bajo que los puntos de cada lado). La línea tangente siempre tiene una pendiente de 0 en estos puntos (una línea horizontal), pero una pendiente cero sola no garantiza un punto extremo. He aquí cómo encontrarlos:[3]  2 Encuentra la ecuación de lo normal. La "normal" a una curva en un punto particular pasa a través de ese punto, pero tiene una pendiente perpendicular a una tangente. Para encontrar la ecuación para lo normal, aproveche el hecho de que (pendiente de tangente) (pendiente de lo normal) = -1, cuando ambos pasan por el mismo punto en el gráfico.[4] En otras palabras:
2 Encuentra la ecuación de lo normal. La "normal" a una curva en un punto particular pasa a través de ese punto, pero tiene una pendiente perpendicular a una tangente. Para encontrar la ecuación para lo normal, aproveche el hecho de que (pendiente de tangente) (pendiente de lo normal) = -1, cuando ambos pasan por el mismo punto en el gráfico.[4] En otras palabras: