El perímetro es una medida del área o distancia alrededor de una forma bidimensional. En un rectángulo, por ejemplo, el perímetro es la longitud total del contorno del rectángulo, incluidos los dos bordes a lo ancho y los dos bordes longitudinales. Para determinar el perímetro de una forma, por lo tanto, se suman todas las dimensiones que componen el borde exterior de la forma. Poder encontrar el perímetro de una forma tiene muchas aplicaciones en el mundo real. Digamos, por ejemplo, que quería construir una valla alrededor de su patio trasero. Para comprar materiales, debe saber la cantidad de cercas que necesitará y determinar que debe determinar el perímetro del área que desea rodear.
Parte uno de dos:
Encontrar el perímetro de la mayoría de las formas
-
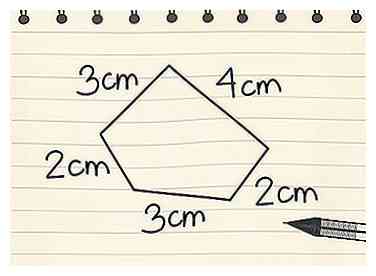 1 Determine la longitud de cada lado. Como el perímetro es solo una medida del contorno de una figura bidimensional, generalmente no necesita una fórmula específica para encontrar el perímetro (aunque hay ecuaciones para formas específicas que lo hacen más fácil). Sin embargo, necesitas saber la longitud de todos los lados de la forma.[1]
1 Determine la longitud de cada lado. Como el perímetro es solo una medida del contorno de una figura bidimensional, generalmente no necesita una fórmula específica para encontrar el perímetro (aunque hay ecuaciones para formas específicas que lo hacen más fácil). Sin embargo, necesitas saber la longitud de todos los lados de la forma.[1] - Por ejemplo, un pentágono tiene cinco lados, y usted necesita saber la longitud de cada uno para determinar el perímetro.
- Incluso con un polígono irregular que tiene 20 lados, aún puede encontrar el perímetro siempre que sepa la longitud de cada lado.
-
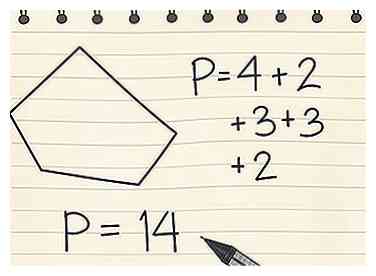 2 Agregue la longitud de todos los lados juntos. Para encontrar el perímetro de objetos no circulares, encuentre la suma de todas las longitudes de los lados para determinar la distancia alrededor de la forma.[2]
2 Agregue la longitud de todos los lados juntos. Para encontrar el perímetro de objetos no circulares, encuentre la suma de todas las longitudes de los lados para determinar la distancia alrededor de la forma.[2] - Supongamos que el pentágono irregular tiene las siguientes longitudes: A = 4, B = 2, C = 3, D = 3 y E = 2
- Agregue 4 + 2 + 3 + 3 + 2 = 14, donde P (perímetro) = 14
-
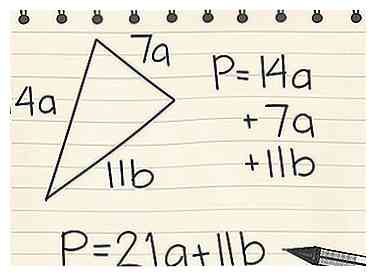 3 Tratar con variables Aún puede encontrar el perímetro cuando trabaja con variables. Por ejemplo, supongamos que tiene un triángulo con las longitudes laterales 14a, 11b y 7a:[3]
3 Tratar con variables Aún puede encontrar el perímetro cuando trabaja con variables. Por ejemplo, supongamos que tiene un triángulo con las longitudes laterales 14a, 11b y 7a:[3] - Encuentre la suma de todos los lados: P = 14a + 11b + 7a
- Combina los términos similares: P = (14a + 7a) + 11b
- P = 21a + 11b
-
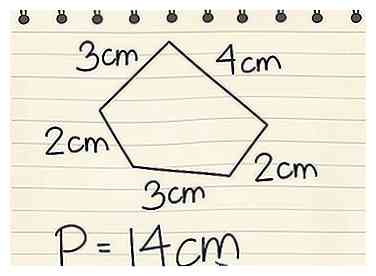 4 Presta atención a las unidades de medida. En una aplicación del mundo real, encontrar el perímetro de un objeto no te servirá de mucho si no sabes con qué unidad de medida estás trabajando (como pies, millas o metros). Con el pentágono, si cada lado se midió en centímetros, entonces sabes que P = 14 cm.
4 Presta atención a las unidades de medida. En una aplicación del mundo real, encontrar el perímetro de un objeto no te servirá de mucho si no sabes con qué unidad de medida estás trabajando (como pies, millas o metros). Con el pentágono, si cada lado se midió en centímetros, entonces sabes que P = 14 cm.
Parte dos de dos:
Aprendizaje de fórmulas perimétricas
-
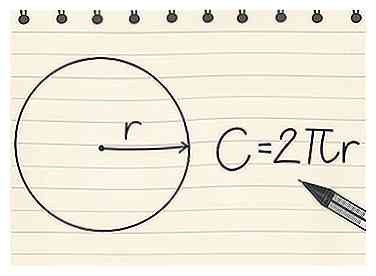 1 Encuentra el perímetro de un círculo. Algunas formas regulares tienen fórmulas que hacen que sea más rápido encontrar el perímetro de la figura. Pero hay otras formas, como círculos, que requieren una fórmula para encontrar el perímetro. El perímetro de un círculo se llama circunferencia. Para encontrar la circunferencia de un círculo, usa la ecuación C (circunferencia) = 2πr.[4]
1 Encuentra el perímetro de un círculo. Algunas formas regulares tienen fórmulas que hacen que sea más rápido encontrar el perímetro de la figura. Pero hay otras formas, como círculos, que requieren una fórmula para encontrar el perímetro. El perímetro de un círculo se llama circunferencia. Para encontrar la circunferencia de un círculo, usa la ecuación C (circunferencia) = 2πr.[4] - Para comenzar, encuentre el radio del círculo, que es la longitud de un segmento de línea que va del centro del círculo al perímetro.
- Para ecuaciones más simples, use la versión truncada π = 3.14
- Para un círculo con un radio de 4 cm: C = 2 x 3.14 x 4 = 25.12 cm
-
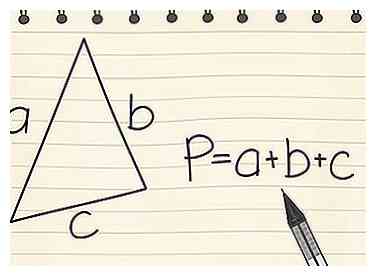 2 Encuentra el perímetro de un triángulo. Usa la ecuación P = a + b + c para un triángulo. Por ejemplo, si un triángulo tiene las dimensiones a = 20 cm, b = 11 cm y c = 9 cm, entonces P = 20 + 11 + 9 = 40 cm.
2 Encuentra el perímetro de un triángulo. Usa la ecuación P = a + b + c para un triángulo. Por ejemplo, si un triángulo tiene las dimensiones a = 20 cm, b = 11 cm y c = 9 cm, entonces P = 20 + 11 + 9 = 40 cm. -
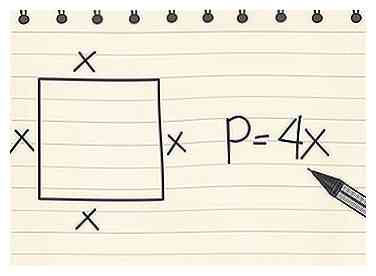 3 Encuentra el perímetro de un cuadrado. Debido a que un cuadrado tiene cuatro lados de la misma longitud, puede usar la ecuación simple P = 4x, donde x es igual a la longitud de un lado.
3 Encuentra el perímetro de un cuadrado. Debido a que un cuadrado tiene cuatro lados de la misma longitud, puede usar la ecuación simple P = 4x, donde x es igual a la longitud de un lado. - En un cuadrado donde x = 3 cm, entonces P = 4 x 3 = 12 cm
-
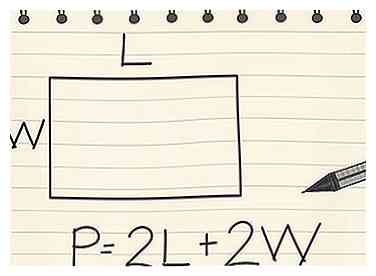 4 Encuentra el perímetro de un rectángulo. Como los lados longitudinales son iguales y los lados anchos son iguales en un rectángulo, puede usar la ecuación P = 2l + 2w, donde l es la longitud de un lado yw es el ancho de un lado. Para un rectángulo donde l = 8cm yw = 5cm:
4 Encuentra el perímetro de un rectángulo. Como los lados longitudinales son iguales y los lados anchos son iguales en un rectángulo, puede usar la ecuación P = 2l + 2w, donde l es la longitud de un lado yw es el ancho de un lado. Para un rectángulo donde l = 8cm yw = 5cm: - P = (2 x 8) + (2 x 5)
- P = 16 + 10
- P = 26 cm
- La ecuación P = 2 (l + h) también le dará el mismo resultado: 2 (8 + 5) = 2 (13) = 26 cm[5]
-
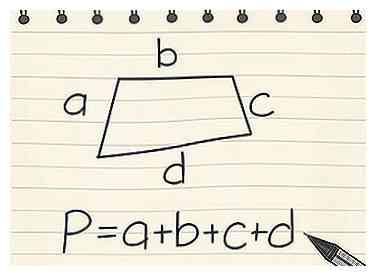 5 Encuentra el perímetro de otros cuadriláteros. Un cuadrilátero se refiere a cualquier forma bidimensional con cuatro lados cerrados y rectos. Esto incluye rectángulos, cuadrados, trapezoides, paralelogramos, cometas y rombos.[6] Hay tres ecuaciones que puedes usar para un cuadrilátero, dependiendo de los lados:
5 Encuentra el perímetro de otros cuadriláteros. Un cuadrilátero se refiere a cualquier forma bidimensional con cuatro lados cerrados y rectos. Esto incluye rectángulos, cuadrados, trapezoides, paralelogramos, cometas y rombos.[6] Hay tres ecuaciones que puedes usar para un cuadrilátero, dependiendo de los lados: - Para un cuadrilátero sin lados iguales, como un trapecio irregular, use la ecuación P = a + b + c + d
- Para un cuadrilátero con cuatro lados iguales, use la misma ecuación que un cuadrado: P = 4x.
- Para los cuadriláteros donde los lados longitudinales son iguales y los lados anchos son los mismos (como un rectángulo), use las ecuaciones P = 2a + 2b o P = 2 (a + b)
 Minotauromaquia
Minotauromaquia
 1 Determine la longitud de cada lado. Como el perímetro es solo una medida del contorno de una figura bidimensional, generalmente no necesita una fórmula específica para encontrar el perímetro (aunque hay ecuaciones para formas específicas que lo hacen más fácil). Sin embargo, necesitas saber la longitud de todos los lados de la forma.[1]
1 Determine la longitud de cada lado. Como el perímetro es solo una medida del contorno de una figura bidimensional, generalmente no necesita una fórmula específica para encontrar el perímetro (aunque hay ecuaciones para formas específicas que lo hacen más fácil). Sin embargo, necesitas saber la longitud de todos los lados de la forma.[1]  2 Agregue la longitud de todos los lados juntos. Para encontrar el perímetro de objetos no circulares, encuentre la suma de todas las longitudes de los lados para determinar la distancia alrededor de la forma.[2]
2 Agregue la longitud de todos los lados juntos. Para encontrar el perímetro de objetos no circulares, encuentre la suma de todas las longitudes de los lados para determinar la distancia alrededor de la forma.[2]  3 Tratar con variables Aún puede encontrar el perímetro cuando trabaja con variables. Por ejemplo, supongamos que tiene un triángulo con las longitudes laterales 14a, 11b y 7a:[3]
3 Tratar con variables Aún puede encontrar el perímetro cuando trabaja con variables. Por ejemplo, supongamos que tiene un triángulo con las longitudes laterales 14a, 11b y 7a:[3]  4 Presta atención a las unidades de medida. En una aplicación del mundo real, encontrar el perímetro de un objeto no te servirá de mucho si no sabes con qué unidad de medida estás trabajando (como pies, millas o metros). Con el pentágono, si cada lado se midió en centímetros, entonces sabes que P = 14 cm.
4 Presta atención a las unidades de medida. En una aplicación del mundo real, encontrar el perímetro de un objeto no te servirá de mucho si no sabes con qué unidad de medida estás trabajando (como pies, millas o metros). Con el pentágono, si cada lado se midió en centímetros, entonces sabes que P = 14 cm. 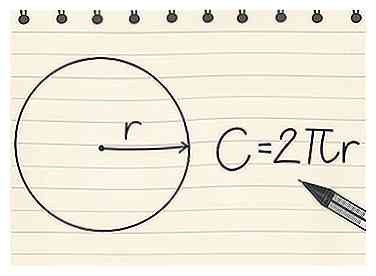 1 Encuentra el perímetro de un círculo. Algunas formas regulares tienen fórmulas que hacen que sea más rápido encontrar el perímetro de la figura. Pero hay otras formas, como círculos, que requieren una fórmula para encontrar el perímetro. El perímetro de un círculo se llama circunferencia. Para encontrar la circunferencia de un círculo, usa la ecuación C (circunferencia) = 2πr.[4]
1 Encuentra el perímetro de un círculo. Algunas formas regulares tienen fórmulas que hacen que sea más rápido encontrar el perímetro de la figura. Pero hay otras formas, como círculos, que requieren una fórmula para encontrar el perímetro. El perímetro de un círculo se llama circunferencia. Para encontrar la circunferencia de un círculo, usa la ecuación C (circunferencia) = 2πr.[4]  2 Encuentra el perímetro de un triángulo. Usa la ecuación P = a + b + c para un triángulo. Por ejemplo, si un triángulo tiene las dimensiones a = 20 cm, b = 11 cm y c = 9 cm, entonces P = 20 + 11 + 9 = 40 cm.
2 Encuentra el perímetro de un triángulo. Usa la ecuación P = a + b + c para un triángulo. Por ejemplo, si un triángulo tiene las dimensiones a = 20 cm, b = 11 cm y c = 9 cm, entonces P = 20 + 11 + 9 = 40 cm. 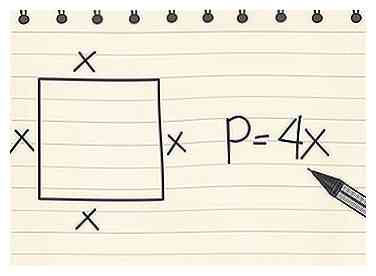 3 Encuentra el perímetro de un cuadrado. Debido a que un cuadrado tiene cuatro lados de la misma longitud, puede usar la ecuación simple P = 4x, donde x es igual a la longitud de un lado.
3 Encuentra el perímetro de un cuadrado. Debido a que un cuadrado tiene cuatro lados de la misma longitud, puede usar la ecuación simple P = 4x, donde x es igual a la longitud de un lado.  4 Encuentra el perímetro de un rectángulo. Como los lados longitudinales son iguales y los lados anchos son iguales en un rectángulo, puede usar la ecuación P = 2l + 2w, donde l es la longitud de un lado yw es el ancho de un lado. Para un rectángulo donde l = 8cm yw = 5cm:
4 Encuentra el perímetro de un rectángulo. Como los lados longitudinales son iguales y los lados anchos son iguales en un rectángulo, puede usar la ecuación P = 2l + 2w, donde l es la longitud de un lado yw es el ancho de un lado. Para un rectángulo donde l = 8cm yw = 5cm:  5 Encuentra el perímetro de otros cuadriláteros. Un cuadrilátero se refiere a cualquier forma bidimensional con cuatro lados cerrados y rectos. Esto incluye rectángulos, cuadrados, trapezoides, paralelogramos, cometas y rombos.[6] Hay tres ecuaciones que puedes usar para un cuadrilátero, dependiendo de los lados:
5 Encuentra el perímetro de otros cuadriláteros. Un cuadrilátero se refiere a cualquier forma bidimensional con cuatro lados cerrados y rectos. Esto incluye rectángulos, cuadrados, trapezoides, paralelogramos, cometas y rombos.[6] Hay tres ecuaciones que puedes usar para un cuadrilátero, dependiendo de los lados: