Cualquiera puede aprender matemáticas, ya sea que esté en matemática superior en la escuela o simplemente esté buscando repasar lo básico. Después de discutir formas de ser un buen estudiante de matemáticas, este artículo le enseñará la progresión básica de los cursos de matemáticas y le dará los elementos básicos que deberá aprender en cada curso. Luego, el artículo abordará los aspectos básicos del aprendizaje de la aritmética, lo que ayudará a los niños de la escuela primaria y a cualquier otra persona que necesite repasar los fundamentos.
Parte uno de seis:
Claves para ser un buen estudiante de matemáticas
-
 1 Preséntate para la clase. Cuando pierdes la clase, tienes que aprender los conceptos ya sea de un compañero de clase o de tu libro de texto. Nunca obtendrá una visión general tan buena de sus amigos o del texto como lo hará de su maestro.
1 Preséntate para la clase. Cuando pierdes la clase, tienes que aprender los conceptos ya sea de un compañero de clase o de tu libro de texto. Nunca obtendrá una visión general tan buena de sus amigos o del texto como lo hará de su maestro. - Ven a clases a tiempo. De hecho, venga un poco temprano y abra su cuaderno en el lugar correcto, abra su libro de texto y saque su calculadora para que esté listo para comenzar cuando su maestro esté listo para comenzar.
- Solo saltea la clase si estás enfermo. Cuando se pierda la clase, hable con un compañero de clase para averiguar de qué habló la maestra y qué deberes se le asignaron.
-
 2 Trabaja junto con tu maestro. Si tu profesor tiene problemas al principio de tu clase, entonces trabaja junto con el profesor en tu cuaderno.
2 Trabaja junto con tu maestro. Si tu profesor tiene problemas al principio de tu clase, entonces trabaja junto con el profesor en tu cuaderno. - Asegúrese de que sus notas sean claras y fáciles de leer. No solo escribas los problemas. También anote todo lo que el maestro dice que aumenta su comprensión de los conceptos.
- Trabaje cualquier problema de muestra que su profesor publique para que usted haga. Cuando el docente camine por el aula mientras trabaja, responda las preguntas.
- Participa mientras el maestro está trabajando un problema. No esperes a que tu maestra te llame. Ofrézcase como voluntario para responder cuando sepa la respuesta y levante la mano para hacer preguntas cuando no esté seguro de lo que se enseña.
-
 3 Haga su tarea el mismo día que se le asignó. Cuando haces la tarea el mismo día, los conceptos están frescos en tu mente. Algunas veces, terminar la tarea el mismo día no es posible. Solo asegúrese de que su tarea esté completa antes de ir a clase.
3 Haga su tarea el mismo día que se le asignó. Cuando haces la tarea el mismo día, los conceptos están frescos en tu mente. Algunas veces, terminar la tarea el mismo día no es posible. Solo asegúrese de que su tarea esté completa antes de ir a clase. -
 4 Haga un esfuerzo fuera de la clase si necesita ayuda. Vaya a su maestro durante su período libre o durante el horario de oficina.
4 Haga un esfuerzo fuera de la clase si necesita ayuda. Vaya a su maestro durante su período libre o durante el horario de oficina. - Si tiene un Centro de Matemáticas en su escuela, averigüe las horas que está abierto y obtenga ayuda.
- Únete a un grupo de estudio. Los buenos grupos de estudio generalmente contienen 4 o 5 personas en una buena combinación de niveles de habilidad. Si eres un estudiante "C" en matemáticas, únete a un grupo que tiene 2 o 3 estudiantes "A" o "B" para que puedas subir tu nivel. Evite unirse a un grupo lleno de estudiantes cuyas calificaciones son más bajas que las suyas.[1]
Parte dos de seis:
Aprender matemáticas en la escuela
-
 1 Comience con aritmética. En la mayoría de las escuelas, los estudiantes trabajan en aritmética durante los grados de primaria. La aritmética incluye los fundamentos de suma, resta, multiplicación y división.
1 Comience con aritmética. En la mayoría de las escuelas, los estudiantes trabajan en aritmética durante los grados de primaria. La aritmética incluye los fundamentos de suma, resta, multiplicación y división. - Trabaja en simulacros. Hacer una gran cantidad de problemas aritméticos una y otra vez es la mejor manera de entender los fundamentos. Busque software que le proporcione muchos problemas matemáticos diferentes para trabajar. Además, busque ejercicios cronometrados para aumentar su velocidad.
- La repetición es la base de las matemáticas. ¡El concepto no solo debe aprenderse, sino ponerse a trabajar para que lo recuerde!
- También puede encontrar simulacros aritméticos en línea, y puede descargar aplicaciones aritméticas en su dispositivo móvil.
-
 2 Progreso al preálgebra. Este curso proporcionará los elementos básicos que necesitarás para resolver problemas de álgebra más adelante.
2 Progreso al preálgebra. Este curso proporcionará los elementos básicos que necesitarás para resolver problemas de álgebra más adelante. - Aprende sobre fracciones y decimales. Aprenderá a sumar, restar, multiplicar y dividir fracciones y decimales. En cuanto a las fracciones, aprenderás cómo reducir fracciones e interpretar números mixtos. Con respecto a los decimales, comprenderá el valor posicional, y podrá usar decimales en problemas verbales.
- Proporciones de estudio, proporciones y porcentajes. Estos conceptos te ayudarán a aprender a hacer comparaciones.
- Resuelve cuadrados y raíces cuadradas. Cuando hayas dominado este tema, tendrás cuadrados perfectos de muchos números memorizados. También podrá trabajar con ecuaciones que contengan raíces cuadradas.
- Preséntese a la geometría básica. Aprenderás todas las formas y conceptos 3D. También aprenderá conceptos como área, perímetro, volumen y área de superficie, así como información sobre líneas y ángulos paralelos y perpendiculares.
- Comprenda algunas estadísticas básicas. En preálgebra, su introducción a las estadísticas incluye principalmente elementos visuales como gráficos, diagramas de dispersión, diagramas de tallo y hojas e histogramas.
- Aprende los conceptos básicos de álgebra. Estos incluirán conceptos como resolver ecuaciones simples que contienen variables, aprender sobre propiedades como la propiedad distributiva, graficar ecuaciones simples y resolver desigualdades.
-
 3 Avance a Algebra I. En su primer año de álgebra, aprenderá sobre los símbolos básicos que participan en el álgebra. También aprenderás a:
3 Avance a Algebra I. En su primer año de álgebra, aprenderá sobre los símbolos básicos que participan en el álgebra. También aprenderás a: - Resuelve ecuaciones lineales y desigualdades que contienen 1-2 variables. Aprenderá cómo resolver estos problemas no solo en papel, sino también en una calculadora.
- Abordar los problemas planteados Se sorprenderá de cuántos problemas diarios que enfrentará en el futuro implican la capacidad de resolver problemas de enunciado algebraico. Por ejemplo, usará álgebra para calcular la tasa de interés que gana en su cuenta bancaria o en sus inversiones. También puede usar álgebra para calcular cuánto tiempo tendrá que viajar en función de la velocidad de su automóvil.
- Trabaja con exponentes. Cuando comiences a resolver ecuaciones con polinomios (expresiones que contienen tanto números como variables), tendrás que entender cómo usar exponentes. Esto también puede incluir trabajar con notación científica.Una vez que tenga los exponentes abajo, puede aprender a sumar, restar, multiplicar y dividir expresiones polinomiales.
- Comprender funciones y gráficos. En álgebra, realmente te meterás en ecuaciones gráficas. Aprenderá cómo calcular la pendiente de una línea, cómo poner ecuaciones en forma de punto y pendiente, y cómo calcular las intersecciones en xey de una línea usando la forma pendiente-intersección.
- Calcule los sistemas de ecuaciones. A veces, te dan 2 ecuaciones separadas con variables xey, y tienes que resolver x o y para ambas ecuaciones. Afortunadamente, aprenderá muchos trucos para resolver estas ecuaciones, incluidas las gráficas, la sustitución y la suma.[2]
-
 4 Entrar en la geometría En geometría, aprenderá sobre las propiedades de líneas, segmentos, ángulos y formas.[3]
4 Entrar en la geometría En geometría, aprenderá sobre las propiedades de líneas, segmentos, ángulos y formas.[3] - Memorizará una serie de teoremas y corolarios que lo ayudarán a comprender las reglas de la geometría.
- Aprenderá cómo calcular el área de un círculo, cómo usar el teorema de Pitágoras y cómo descubrir las relaciones entre los ángulos y los lados de triángulos especiales.
- Verá mucha geometría en futuras pruebas estandarizadas como SAT, ACT y GRE.
-
 5 Enfréntate a Algebra II. Algebra II se basa en los conceptos que aprendió en Algebra I, pero agrega temas más complejos que involucran matrices y funciones no lineales más complejas.
5 Enfréntate a Algebra II. Algebra II se basa en los conceptos que aprendió en Algebra I, pero agrega temas más complejos que involucran matrices y funciones no lineales más complejas. -
 6 Tackle trigonometry. Conoces las palabras de trig: seno, coseno, tangente, etc. La trigonometría te enseñará muchas formas prácticas de calcular ángulos y longitudes de líneas, y estas habilidades serán muy valiosas para las personas que se dedican a la construcción, arquitectura, ingeniería o topografía.
6 Tackle trigonometry. Conoces las palabras de trig: seno, coseno, tangente, etc. La trigonometría te enseñará muchas formas prácticas de calcular ángulos y longitudes de líneas, y estas habilidades serán muy valiosas para las personas que se dedican a la construcción, arquitectura, ingeniería o topografía. -
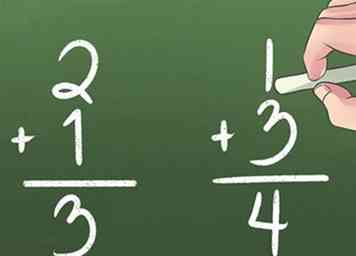 7 Cuente con algunos cálculos. El cálculo puede sonar intimidante, pero es una herramienta increíble para entender tanto el comportamiento de los números como el mundo que lo rodea.
7 Cuente con algunos cálculos. El cálculo puede sonar intimidante, pero es una herramienta increíble para entender tanto el comportamiento de los números como el mundo que lo rodea. - Cálculo le enseñará sobre funciones y sobre límites. Verá el comportamiento o una serie de funciones útiles, incluidas e ^ x y funciones logarítmicas.
- También aprenderá cómo calcular y trabajar con derivados. Una primera derivada le proporciona información basada en la pendiente de una línea tangente a una ecuación. Por ejemplo, una derivada te dice la velocidad a la que algo está cambiando en una situación no lineal. Una segunda derivada le indicará si una función está aumentando o disminuyendo a lo largo de un determinado intervalo, de modo que puede determinar la concavidad de una función.
- Las integrales le enseñarán a calcular el área debajo de una curva así como también el volumen.
- El cálculo de la escuela secundaria generalmente termina con secuencias y series. Aunque los estudiantes no verán muchas aplicaciones para series, son importantes para las personas que continúan estudiando ecuaciones diferenciales.
- El cálculo aún es solo el comienzo para algunos. Si estás considerando una carrera con una alta participación de las matemáticas y la ciencia, como un ingeniero, ¡intenta ir un poco más lejos![4]
Parte tres de seis:
Fundamentos matemáticos - As Some Addition
-
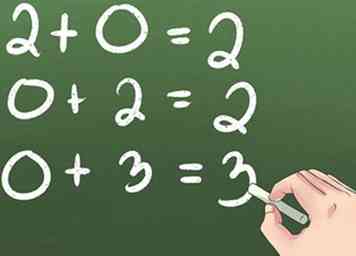 1 Comience con hechos "+1". Agregar 1 a un número lo lleva al siguiente número más alto en la línea numérica. Por ejemplo, 2 + 1 = 3.
1 Comience con hechos "+1". Agregar 1 a un número lo lleva al siguiente número más alto en la línea numérica. Por ejemplo, 2 + 1 = 3. -
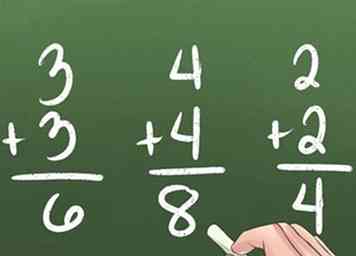 2 Comprender los ceros. Cualquier número agregado a cero equivale al mismo número porque "cero" es lo mismo que "nada".
2 Comprender los ceros. Cualquier número agregado a cero equivale al mismo número porque "cero" es lo mismo que "nada". -
 3 Aprende los dobles. Los dobles son problemas que implican agregar dos del mismo número. Por ejemplo, 3 + 3 = 6 es un ejemplo de una ecuación que implica dobles.
3 Aprende los dobles. Los dobles son problemas que implican agregar dos del mismo número. Por ejemplo, 3 + 3 = 6 es un ejemplo de una ecuación que implica dobles. -
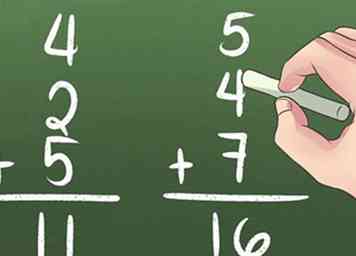 4 Utilice el mapeo para conocer otras soluciones de adición. En el siguiente ejemplo, aprende mapeando lo que sucede cuando agrega 3 a 5, 2 y 1. Pruebe los problemas de "agregar 2" por su cuenta.
4 Utilice el mapeo para conocer otras soluciones de adición. En el siguiente ejemplo, aprende mapeando lo que sucede cuando agrega 3 a 5, 2 y 1. Pruebe los problemas de "agregar 2" por su cuenta. -
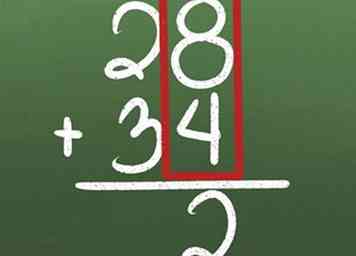 5 Ir más allá de 10. Aprenda a sumar 3 números para obtener un número mayor a 10.
5 Ir más allá de 10. Aprenda a sumar 3 números para obtener un número mayor a 10. -
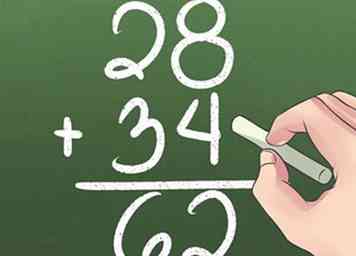 6 Agrega números más grandes. Aprenda a reagrupar 1s en el lugar 10s, 10s en el lugar 100s, etc.
6 Agrega números más grandes. Aprenda a reagrupar 1s en el lugar 10s, 10s en el lugar 100s, etc. - Agregue los números en la columna de la derecha primero. 8 + 4 = 12, lo que significa que tiene 1 10 y 2 1s. Escriba el 2 debajo de la columna 1s.
- Escribe la columna 1 sobre los 10s.
- Agregue la columna 10s juntas.
Parte cuatro de seis:
Fundamentos matemáticos: estrategias para restar
-
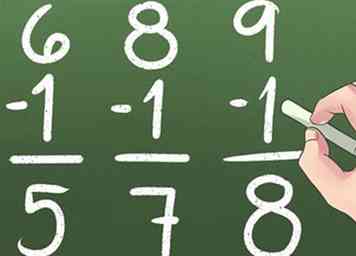 1 Comience con "al revés 1."Restar 1 de un número lo lleva hacia atrás 1 número. Por ejemplo, 4 - 1 = 3.
1 Comience con "al revés 1."Restar 1 de un número lo lleva hacia atrás 1 número. Por ejemplo, 4 - 1 = 3. -
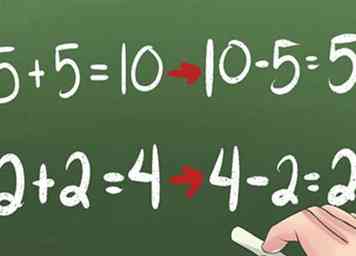 2 Aprende la resta de dobles. Por ejemplo, agregue los dobles 5 + 5 para obtener 10. Simplemente escriba la ecuación hacia atrás para obtener 10 - 5 = 5.
2 Aprende la resta de dobles. Por ejemplo, agregue los dobles 5 + 5 para obtener 10. Simplemente escriba la ecuación hacia atrás para obtener 10 - 5 = 5. - Si 5 + 5 = 10, entonces 10 - 5 = 5.
- Si 2 + 2 = 4, entonces 4 - 2 = 2.
-
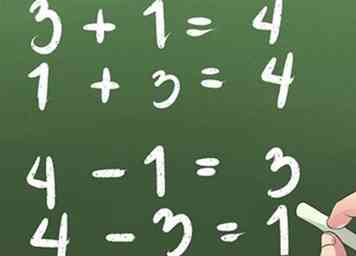 3 Memorice familias de hechos Por ejemplo:
3 Memorice familias de hechos Por ejemplo: - 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1
-
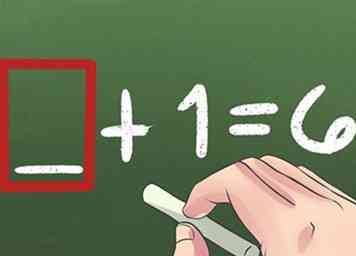 4 Encuentra los números que faltan Por ejemplo, ___ + 1 = 6 (la respuesta es 5). Esto también sienta las bases para el álgebra y más allá.
4 Encuentra los números que faltan Por ejemplo, ___ + 1 = 6 (la respuesta es 5). Esto también sienta las bases para el álgebra y más allá. -
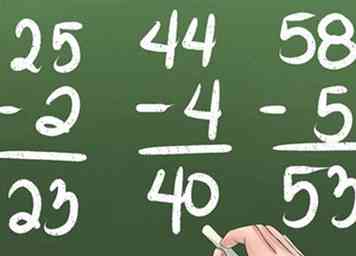 5 Memoriza las restas hasta 20.
5 Memoriza las restas hasta 20. -
 6 Practica restar números de 1 dígito de números de 2 dígitos sin pedir prestado. Reste los números en la columna 1s y disminuya el número en la columna 10s.
6 Practica restar números de 1 dígito de números de 2 dígitos sin pedir prestado. Reste los números en la columna 1s y disminuya el número en la columna 10s. -
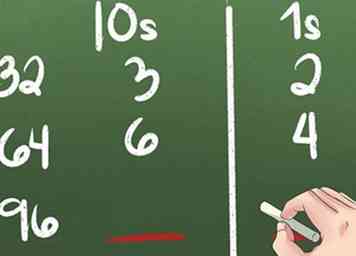 7 Practique el valor posicional para prepararse para restar con endeudamiento.
7 Practique el valor posicional para prepararse para restar con endeudamiento. - 32 = 3 10s y 2 1s.
- 64 = 6 10s y 4 1s.
- 96 = __ 10s y __ 1s.
-
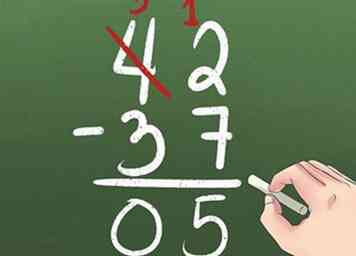 8 Reste con préstamos.
8 Reste con préstamos. - Quiere restar 42 - 37. Comienza tratando de restar 2 - 7 en la columna 1s. Sin embargo, eso no funciona!
- Pedir prestado 10 de la columna 10s y ponerlo en la columna 1s. En lugar de 4 10s, ahora tienes 3 10s. En lugar de 2 1s, ahora tiene 12 1.
- Reste primero su columna 1s: 12 - 7 = 5. Luego, revise la columna 10s. Como 3 - 3 = 0, no tiene que escribir 0. Su respuesta es 5.[5]
Parte cinco de seis:
Fundamentos matemáticos - Multiplicación maestra
-
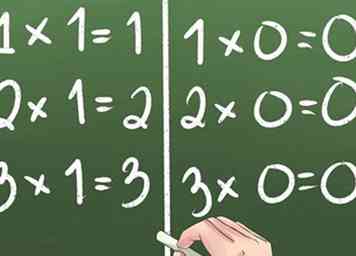 1 Comience con 1s y 0s. Cualquier número multiplicado por 1 es igual a sí mismo. Cualquier número por cero es igual a cero.
1 Comience con 1s y 0s. Cualquier número multiplicado por 1 es igual a sí mismo. Cualquier número por cero es igual a cero. -
 2 Memoriza la tabla de multiplicar
2 Memoriza la tabla de multiplicar -
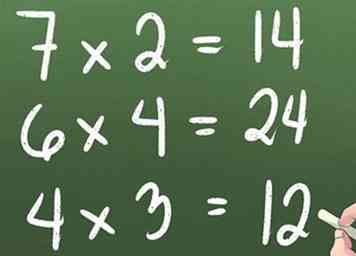 3Practica problemas de multiplicación de un solo dígito
3Practica problemas de multiplicación de un solo dígito -
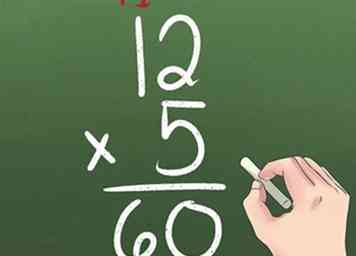 4 Multiplica números de 2 dígitos por números de 1 dígito.
4 Multiplica números de 2 dígitos por números de 1 dígito. - Multiplica el número inferior derecho por el número superior derecho.
- Multiplica el número inferior derecho por el número superior izquierdo.
-
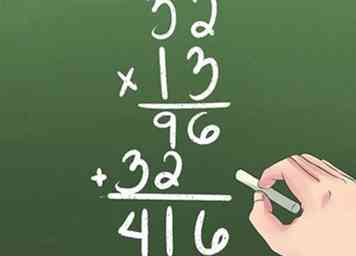 5 Multiplica 2 números de 2 dígitos.
5 Multiplica 2 números de 2 dígitos. - Multiplique el número inferior derecho por la parte superior derecha y luego los números superiores izquierdos.
- Mueva la segunda fila un dígito a la izquierda.
- Multiplica el número inferior izquierdo por la esquina superior derecha y luego los números superiores izquierdos.
- Agrega las columnas juntas.
-
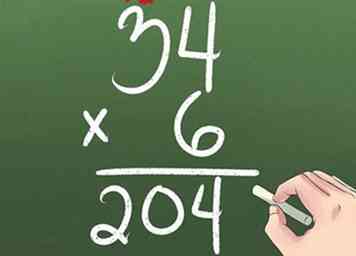 6 Multiplica y reagrupa las columnas.
6 Multiplica y reagrupa las columnas. - Desea multiplicar 34 x 6. Comienza multiplicando la columna de 1s (4 x 6), pero no puede tener 24 1 en la columna de 1s.
- Mantenga 4 1s en la columna de 1s. Mueve los 2 10s a la columna de 10s.
- Multiplica 6 x 3, lo que equivale a 18. Agrega los 2 que llevaste encima, que equivaldrán a 20.
Parte seis de seis:
Fundamentos matemáticos - Discover Division
-
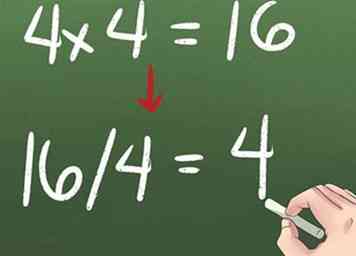 1 Piense en la división como lo opuesto a la multiplicación. Si 4 x 4 = 16, entonces 16/4 = 4.
1 Piense en la división como lo opuesto a la multiplicación. Si 4 x 4 = 16, entonces 16/4 = 4. -
 2 Escribe tu problema de división.
2 Escribe tu problema de división. - Divida el número a la izquierda del símbolo de división, o el divisor, en el primer número debajo del símbolo de división. Como 6/2 = 3, escribirá 3 encima del símbolo de división.
- Multiplica el número sobre el símbolo de división por el divisor. Baja el producto debajo del primer número debajo del símbolo de división. Dado que 3 x 2 = 6, entonces traerá un 6 hacia abajo.
- Reste los 2 números que ha escrito. 6 - 6 = 0. También puede dejar el 0 en blanco, ya que normalmente no comienza un nuevo número con 0.
- Trae el segundo número que está debajo del símbolo de división hacia abajo.
- Divida el número que derribó el divisor. En este caso, 8/2 = 4. Escribe 4 en la parte superior del símbolo de división.
- Multiplique el número superior derecho por el divisor y disminuya el número. 4 x 2 = 8.
- Reste los números. La resta final es igual a cero, lo que significa que ha terminado el problema. 68/2 = 34.[6]
-
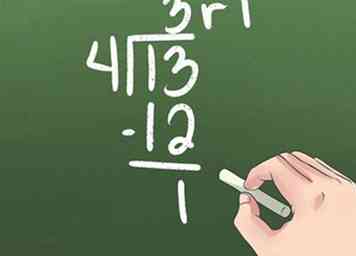 3 Cuenta para los residuos. Algunos divisores no se dividirán uniformemente en otros números. Cuando hayas terminado tu resta final, y no tengas más números para derribar, entonces el número final es tu resto.[7]
3 Cuenta para los residuos. Algunos divisores no se dividirán uniformemente en otros números. Cuando hayas terminado tu resta final, y no tengas más números para derribar, entonces el número final es tu resto.[7]
 Minotauromaquia
Minotauromaquia
 1 Preséntate para la clase. Cuando pierdes la clase, tienes que aprender los conceptos ya sea de un compañero de clase o de tu libro de texto. Nunca obtendrá una visión general tan buena de sus amigos o del texto como lo hará de su maestro.
1 Preséntate para la clase. Cuando pierdes la clase, tienes que aprender los conceptos ya sea de un compañero de clase o de tu libro de texto. Nunca obtendrá una visión general tan buena de sus amigos o del texto como lo hará de su maestro.  2 Trabaja junto con tu maestro. Si tu profesor tiene problemas al principio de tu clase, entonces trabaja junto con el profesor en tu cuaderno.
2 Trabaja junto con tu maestro. Si tu profesor tiene problemas al principio de tu clase, entonces trabaja junto con el profesor en tu cuaderno.  3 Haga su tarea el mismo día que se le asignó. Cuando haces la tarea el mismo día, los conceptos están frescos en tu mente. Algunas veces, terminar la tarea el mismo día no es posible. Solo asegúrese de que su tarea esté completa antes de ir a clase.
3 Haga su tarea el mismo día que se le asignó. Cuando haces la tarea el mismo día, los conceptos están frescos en tu mente. Algunas veces, terminar la tarea el mismo día no es posible. Solo asegúrese de que su tarea esté completa antes de ir a clase.  4 Haga un esfuerzo fuera de la clase si necesita ayuda. Vaya a su maestro durante su período libre o durante el horario de oficina.
4 Haga un esfuerzo fuera de la clase si necesita ayuda. Vaya a su maestro durante su período libre o durante el horario de oficina.  1 Comience con aritmética. En la mayoría de las escuelas, los estudiantes trabajan en aritmética durante los grados de primaria. La aritmética incluye los fundamentos de suma, resta, multiplicación y división.
1 Comience con aritmética. En la mayoría de las escuelas, los estudiantes trabajan en aritmética durante los grados de primaria. La aritmética incluye los fundamentos de suma, resta, multiplicación y división.  2 Progreso al preálgebra. Este curso proporcionará los elementos básicos que necesitarás para resolver problemas de álgebra más adelante.
2 Progreso al preálgebra. Este curso proporcionará los elementos básicos que necesitarás para resolver problemas de álgebra más adelante.  3 Avance a Algebra I. En su primer año de álgebra, aprenderá sobre los símbolos básicos que participan en el álgebra. También aprenderás a:
3 Avance a Algebra I. En su primer año de álgebra, aprenderá sobre los símbolos básicos que participan en el álgebra. También aprenderás a:  4 Entrar en la geometría En geometría, aprenderá sobre las propiedades de líneas, segmentos, ángulos y formas.[3]
4 Entrar en la geometría En geometría, aprenderá sobre las propiedades de líneas, segmentos, ángulos y formas.[3]  5 Enfréntate a Algebra II. Algebra II se basa en los conceptos que aprendió en Algebra I, pero agrega temas más complejos que involucran matrices y funciones no lineales más complejas.
5 Enfréntate a Algebra II. Algebra II se basa en los conceptos que aprendió en Algebra I, pero agrega temas más complejos que involucran matrices y funciones no lineales más complejas.  6 Tackle trigonometry. Conoces las palabras de trig: seno, coseno, tangente, etc. La trigonometría te enseñará muchas formas prácticas de calcular ángulos y longitudes de líneas, y estas habilidades serán muy valiosas para las personas que se dedican a la construcción, arquitectura, ingeniería o topografía.
6 Tackle trigonometry. Conoces las palabras de trig: seno, coseno, tangente, etc. La trigonometría te enseñará muchas formas prácticas de calcular ángulos y longitudes de líneas, y estas habilidades serán muy valiosas para las personas que se dedican a la construcción, arquitectura, ingeniería o topografía. 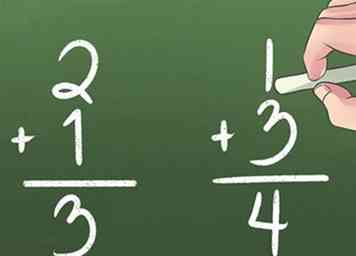 7 Cuente con algunos cálculos. El cálculo puede sonar intimidante, pero es una herramienta increíble para entender tanto el comportamiento de los números como el mundo que lo rodea.
7 Cuente con algunos cálculos. El cálculo puede sonar intimidante, pero es una herramienta increíble para entender tanto el comportamiento de los números como el mundo que lo rodea. 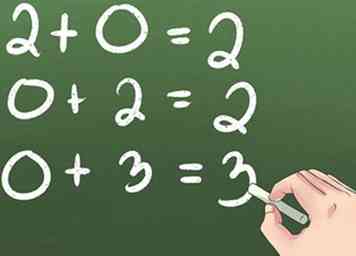 1 Comience con hechos "+1". Agregar 1 a un número lo lleva al siguiente número más alto en la línea numérica. Por ejemplo, 2 + 1 = 3.
1 Comience con hechos "+1". Agregar 1 a un número lo lleva al siguiente número más alto en la línea numérica. Por ejemplo, 2 + 1 = 3. 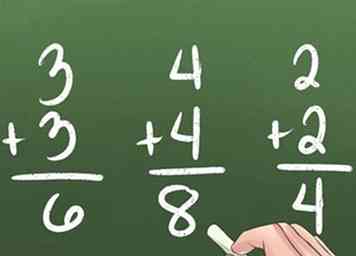 2 Comprender los ceros. Cualquier número agregado a cero equivale al mismo número porque "cero" es lo mismo que "nada".
2 Comprender los ceros. Cualquier número agregado a cero equivale al mismo número porque "cero" es lo mismo que "nada".  3 Aprende los dobles. Los dobles son problemas que implican agregar dos del mismo número. Por ejemplo, 3 + 3 = 6 es un ejemplo de una ecuación que implica dobles.
3 Aprende los dobles. Los dobles son problemas que implican agregar dos del mismo número. Por ejemplo, 3 + 3 = 6 es un ejemplo de una ecuación que implica dobles. 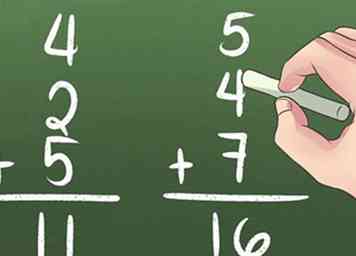 4 Utilice el mapeo para conocer otras soluciones de adición. En el siguiente ejemplo, aprende mapeando lo que sucede cuando agrega 3 a 5, 2 y 1. Pruebe los problemas de "agregar 2" por su cuenta.
4 Utilice el mapeo para conocer otras soluciones de adición. En el siguiente ejemplo, aprende mapeando lo que sucede cuando agrega 3 a 5, 2 y 1. Pruebe los problemas de "agregar 2" por su cuenta. 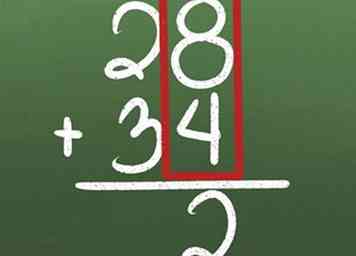 5 Ir más allá de 10. Aprenda a sumar 3 números para obtener un número mayor a 10.
5 Ir más allá de 10. Aprenda a sumar 3 números para obtener un número mayor a 10. 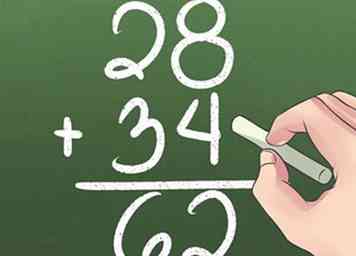 6 Agrega números más grandes. Aprenda a reagrupar 1s en el lugar 10s, 10s en el lugar 100s, etc.
6 Agrega números más grandes. Aprenda a reagrupar 1s en el lugar 10s, 10s en el lugar 100s, etc. 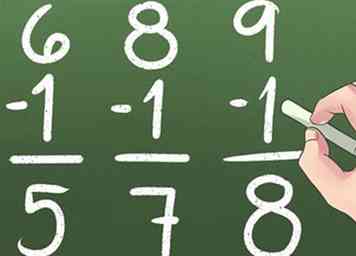 1 Comience con "al revés 1."Restar 1 de un número lo lleva hacia atrás 1 número. Por ejemplo, 4 - 1 = 3.
1 Comience con "al revés 1."Restar 1 de un número lo lleva hacia atrás 1 número. Por ejemplo, 4 - 1 = 3. 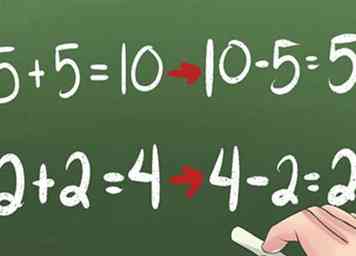 2 Aprende la resta de dobles. Por ejemplo, agregue los dobles 5 + 5 para obtener 10. Simplemente escriba la ecuación hacia atrás para obtener 10 - 5 = 5.
2 Aprende la resta de dobles. Por ejemplo, agregue los dobles 5 + 5 para obtener 10. Simplemente escriba la ecuación hacia atrás para obtener 10 - 5 = 5. 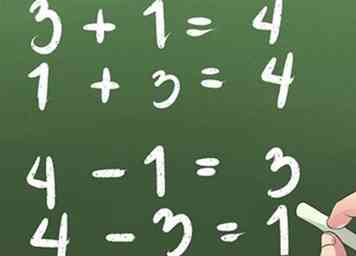 3 Memorice familias de hechos Por ejemplo:
3 Memorice familias de hechos Por ejemplo: 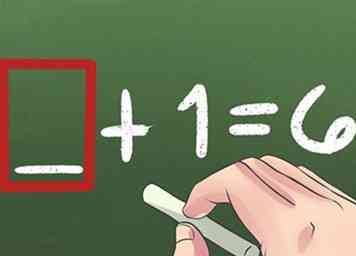 4 Encuentra los números que faltan Por ejemplo, ___ + 1 = 6 (la respuesta es 5). Esto también sienta las bases para el álgebra y más allá.
4 Encuentra los números que faltan Por ejemplo, ___ + 1 = 6 (la respuesta es 5). Esto también sienta las bases para el álgebra y más allá. 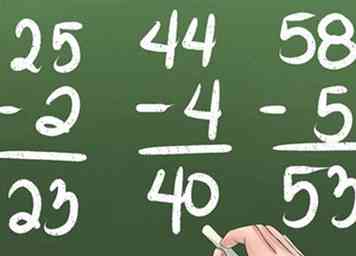 5 Memoriza las restas hasta 20.
5 Memoriza las restas hasta 20.  6 Practica restar números de 1 dígito de números de 2 dígitos sin pedir prestado. Reste los números en la columna 1s y disminuya el número en la columna 10s.
6 Practica restar números de 1 dígito de números de 2 dígitos sin pedir prestado. Reste los números en la columna 1s y disminuya el número en la columna 10s. 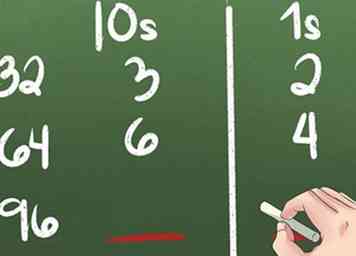 7 Practique el valor posicional para prepararse para restar con endeudamiento.
7 Practique el valor posicional para prepararse para restar con endeudamiento. 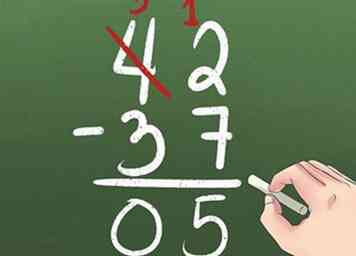 8 Reste con préstamos.
8 Reste con préstamos. 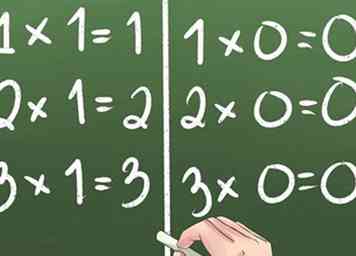 1 Comience con 1s y 0s. Cualquier número multiplicado por 1 es igual a sí mismo. Cualquier número por cero es igual a cero.
1 Comience con 1s y 0s. Cualquier número multiplicado por 1 es igual a sí mismo. Cualquier número por cero es igual a cero.  2 Memoriza la tabla de multiplicar
2 Memoriza la tabla de multiplicar 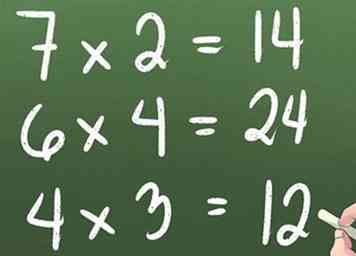 3Practica problemas de multiplicación de un solo dígito
3Practica problemas de multiplicación de un solo dígito 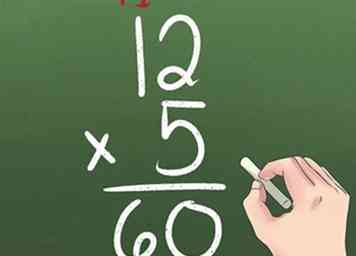 4 Multiplica números de 2 dígitos por números de 1 dígito.
4 Multiplica números de 2 dígitos por números de 1 dígito. 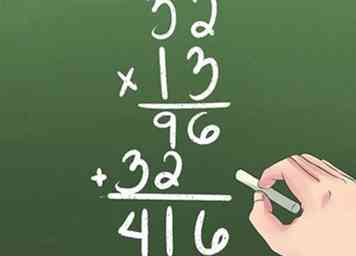 5 Multiplica 2 números de 2 dígitos.
5 Multiplica 2 números de 2 dígitos. 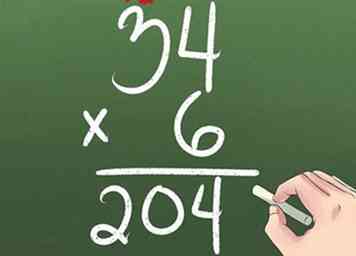 6 Multiplica y reagrupa las columnas.
6 Multiplica y reagrupa las columnas. 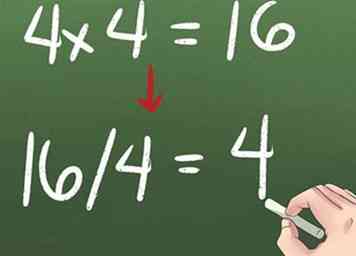 1 Piense en la división como lo opuesto a la multiplicación. Si 4 x 4 = 16, entonces 16/4 = 4.
1 Piense en la división como lo opuesto a la multiplicación. Si 4 x 4 = 16, entonces 16/4 = 4.  2 Escribe tu problema de división.
2 Escribe tu problema de división. 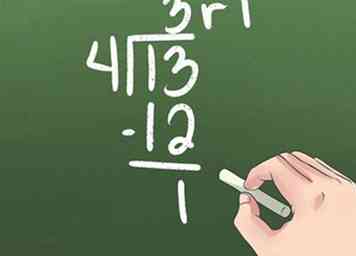 3 Cuenta para los residuos. Algunos divisores no se dividirán uniformemente en otros números. Cuando hayas terminado tu resta final, y no tengas más números para derribar, entonces el número final es tu resto.[7]
3 Cuenta para los residuos. Algunos divisores no se dividirán uniformemente en otros números. Cuando hayas terminado tu resta final, y no tengas más números para derribar, entonces el número final es tu resto.[7]