Los cuadrados mágicos Singly Even Even Order son aquellos que son divisibles por 2 pero no por 4. El cuadrado más antiguo sería cuadrado de orden 6x6, luego tenemos 10x10, 14x14, 18x18, etc.
Pasos
-
 1 PENDIENTE SINGLY EVEN - 6X6 SQUARE.
1 PENDIENTE SINGLY EVEN - 6X6 SQUARE. -
 2 Ahora echemos un vistazo a los cuadrados 6x6. El cuadrado de 6x6 tendrá números del 1 al 36, mientras que el cuadrado de 4x4 tiene números del 1 al 16. 36-16 = 20/2 = 10. Agreguemos 10 a todos los números de cualquier cuadrado de 4x4 para obtener un cuadrado de 4x4 con un total de 74. Este cuadrado de 4x4 lo colocaremos como cuadrados de 2x2 en las 4 esquinas en el cuadro de 6x6 del lado izquierdo. Ahora tenemos números del 1 al 10 y del 27 al 36 para llenar los lugares vacíos.
2 Ahora echemos un vistazo a los cuadrados 6x6. El cuadrado de 6x6 tendrá números del 1 al 36, mientras que el cuadrado de 4x4 tiene números del 1 al 16. 36-16 = 20/2 = 10. Agreguemos 10 a todos los números de cualquier cuadrado de 4x4 para obtener un cuadrado de 4x4 con un total de 74. Este cuadrado de 4x4 lo colocaremos como cuadrados de 2x2 en las 4 esquinas en el cuadro de 6x6 del lado izquierdo. Ahora tenemos números del 1 al 10 y del 27 al 36 para llenar los lugares vacíos. - 11 16 xx xx 21 26 'xx' se trata de lugares por llenar.
- 25 22 xx xx 15 12
- xx xx xx xx xx xx
- xx xx xx xx xx xx
- 18 13 xx xx 24 19
- 20 23 xx xx 14 17
-
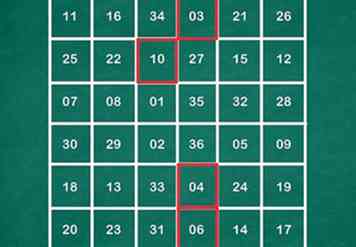
 3 Ahora primero completaremos las diagonales insertando 1 y 36, en una y 2 y 35, en la otra. El resto de los números están tan llenos que tenemos un total de 37 en el resto de los 2 lugares en filas y columnas con un total de 111 en cada una de la tercera y cuarta columnas y filas.
3 Ahora primero completaremos las diagonales insertando 1 y 36, en una y 2 y 35, en la otra. El resto de los números están tan llenos que tenemos un total de 37 en el resto de los 2 lugares en filas y columnas con un total de 111 en cada una de la tercera y cuarta columnas y filas. -
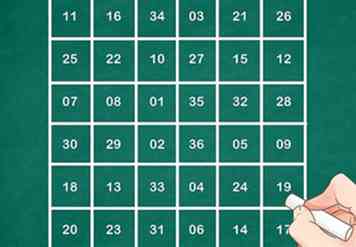 4 El cuadrado completo de 6x6 sería como se muestra a continuación:
4 El cuadrado completo de 6x6 sería como se muestra a continuación: - 11 16 34 03 21 26
- 25 22 10 27 15 12
- 07 08 01 35 32 28
- 30 29 02 36 05 09
- 18 13 33 04 24 19
- 20 23 31 06 14 17
-
 5
5 -
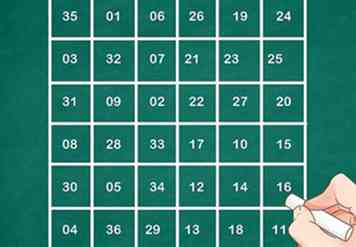 6 Tenemos 880 cuadrados para elegir, además de colocar 3,4,6 y 10 tenemos 24 opciones. Esto se debe a que tenemos 4 opciones para colocar el primer número, 3 opciones para colocar el siguiente número y 2 opciones para el siguiente número. Del mismo modo, para colocar 5,7,8, y 9 tenemos 24 opciones, por lo que obtenemos fácilmente 880x24x24 todos los cuadrados diferentes. Además de las diagonales, tenemos la opción de elegir los números. En lugar de 1 y 2 podríamos haber elegido 9 y 10. Una combinación disponible sería 1,9,10, para una columna y 5,7,8 para la otra, y 3,4,10 para una fila y 2,6 , 9 para la otra fila. ¿Desarrollar otras combinaciones y cada una dará lugar a 880x24x24 nuevos cuadrados de 6x6?
6 Tenemos 880 cuadrados para elegir, además de colocar 3,4,6 y 10 tenemos 24 opciones. Esto se debe a que tenemos 4 opciones para colocar el primer número, 3 opciones para colocar el siguiente número y 2 opciones para el siguiente número. Del mismo modo, para colocar 5,7,8, y 9 tenemos 24 opciones, por lo que obtenemos fácilmente 880x24x24 todos los cuadrados diferentes. Además de las diagonales, tenemos la opción de elegir los números. En lugar de 1 y 2 podríamos haber elegido 9 y 10. Una combinación disponible sería 1,9,10, para una columna y 5,7,8 para la otra, y 3,4,10 para una fila y 2,6 , 9 para la otra fila. ¿Desarrollar otras combinaciones y cada una dará lugar a 880x24x24 nuevos cuadrados de 6x6? -
 7
7 -
 8 Por supuesto, hay otros métodos para calcular los cuadrados de 6x6 y obtener más cuadrados de 6x6. Podríamos haber colocado el cuadrado 4x4 con un total de 74, como un cuadrado central y llenar los números del 1 al 10 y del 27 al 36 en los lugares vacíos en las casillas de las columnas 1st 2nd, 5th and 6th y 1st 2nd, 5th y 6ª filas. También hay otros métodos, intente poner el cuadrado 4x4 con un total de 74 en la 1ª a 4ª filas y columnas y llene las columnas 5ª y 6ª y las filas con los números disponibles. Pruebe otras formas también
8 Por supuesto, hay otros métodos para calcular los cuadrados de 6x6 y obtener más cuadrados de 6x6. Podríamos haber colocado el cuadrado 4x4 con un total de 74, como un cuadrado central y llenar los números del 1 al 10 y del 27 al 36 en los lugares vacíos en las casillas de las columnas 1st 2nd, 5th and 6th y 1st 2nd, 5th y 6ª filas. También hay otros métodos, intente poner el cuadrado 4x4 con un total de 74 en la 1ª a 4ª filas y columnas y llene las columnas 5ª y 6ª y las filas con los números disponibles. Pruebe otras formas también -
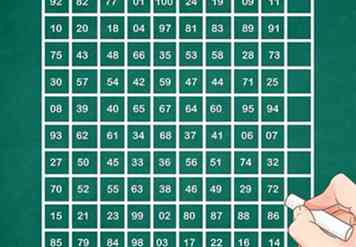
 9 Un cuadrado de pedido de 10x10 tendrá números del 1 al 100 con un total de 505. El cuadrado de orden 6x6 tenía números del 1 al 36. 100-36 = 64, 64/2 es 32. Entonces sumamos 32 a todos los números en el cuadrado de orden 6x6 para obtener uno con un total de 303. Esto se colocará en el centro y los espacios vacíos se llenarán primero con tres cuadrados de 4x4, un cuadrado tendrá números del 9 al 16 y 85 al 92, el segundo de 17 a 24 y 77 a 84 y el tercero de 25 a 32 y de 69 a 76. Ahora habrá Se deben llenar 16 espacios, 8 en las columnas 5, 6 y las filas 1, 2, 9 y 10, y 8 en las filas 5, 6 y las columnas 1, 2, 9 y 10. Tenemos que asegurarnos de que el conjunto de números son tales que en el primer caso las filas suman un total de 101 y en el segundo caso las columnas suman un total de 101, junto con asegurar que el total de la columna sea 202 en el 1er y el total de la fila sea 202 en el segundo caso. Si seleccionamos los números más pequeños con los mismos totales en las columnas y las filas, respectivamente, obtendremos los totales correctos. Es por esta razón que se han seleccionado 1 y 4, 2 y 3, 5 y 8 y 6 y 7.
9 Un cuadrado de pedido de 10x10 tendrá números del 1 al 100 con un total de 505. El cuadrado de orden 6x6 tenía números del 1 al 36. 100-36 = 64, 64/2 es 32. Entonces sumamos 32 a todos los números en el cuadrado de orden 6x6 para obtener uno con un total de 303. Esto se colocará en el centro y los espacios vacíos se llenarán primero con tres cuadrados de 4x4, un cuadrado tendrá números del 9 al 16 y 85 al 92, el segundo de 17 a 24 y 77 a 84 y el tercero de 25 a 32 y de 69 a 76. Ahora habrá Se deben llenar 16 espacios, 8 en las columnas 5, 6 y las filas 1, 2, 9 y 10, y 8 en las filas 5, 6 y las columnas 1, 2, 9 y 10. Tenemos que asegurarnos de que el conjunto de números son tales que en el primer caso las filas suman un total de 101 y en el segundo caso las columnas suman un total de 101, junto con asegurar que el total de la columna sea 202 en el 1er y el total de la fila sea 202 en el segundo caso. Si seleccionamos los números más pequeños con los mismos totales en las columnas y las filas, respectivamente, obtendremos los totales correctos. Es por esta razón que se han seleccionado 1 y 4, 2 y 3, 5 y 8 y 6 y 7. - 92 82 77 01 100 24 19 09 11
- 10 20 18 04 097 81 83 89 91
- 75 43 48 66 035 53 58 28 73
- 30 57 54 42 059 47 44 71 25
- 08 39 40 65 067 64 60 95 94
- 93 62 61 34 068 37 41 06 07
- 27 50 45 33 036 56 51 74 32
- 70 52 55 63 038 46 49 29 72
- 15 21 23 99 002 80 78 88 86
- 85 79 84 98 003 17 22 16 14
- 10 Tenemos la opción de colocar los números del 1 al 8 como queramos. Entonces el número de cuadrados de 6x6 se puede multiplicar por 8x6x4x2 para obtener el número de cuadrados para el cuadrado de 10x10. Por supuesto, hay otras formas de construir los cuadrados de 10x10, por lo que el número de cuadrados posibles solo puede imaginarse.
- 11 Para el cuadrado de 14x14 podemos seguir el mismo procedimiento comenzando con un cuadrado de 10x10 en el que 196-100 = 96, 96/2 = 48, se ha agregado a todos los números para dar un total de 985. El total requerido es 14 (1 + 196) / 2 = 1379. Tendremos que insertar siete cuadrados 4x4 con un total de 394 y llenar los 16 espacios restantes con números del 1 al 8 y del 189 al 196. Podemos colocar los números de 1 a 8 como lo hicimos en el cuadrado de 10x10. Del mismo modo, podemos ir desde el cuadrado de 14x14 hasta el cuadrado de 18x18 y así sucesivamente.
 Minotauromaquia
Minotauromaquia
 1 PENDIENTE SINGLY EVEN - 6X6 SQUARE.
1 PENDIENTE SINGLY EVEN - 6X6 SQUARE.  2 Ahora echemos un vistazo a los cuadrados 6x6. El cuadrado de 6x6 tendrá números del 1 al 36, mientras que el cuadrado de 4x4 tiene números del 1 al 16. 36-16 = 20/2 = 10. Agreguemos 10 a todos los números de cualquier cuadrado de 4x4 para obtener un cuadrado de 4x4 con un total de 74. Este cuadrado de 4x4 lo colocaremos como cuadrados de 2x2 en las 4 esquinas en el cuadro de 6x6 del lado izquierdo. Ahora tenemos números del 1 al 10 y del 27 al 36 para llenar los lugares vacíos.
2 Ahora echemos un vistazo a los cuadrados 6x6. El cuadrado de 6x6 tendrá números del 1 al 36, mientras que el cuadrado de 4x4 tiene números del 1 al 16. 36-16 = 20/2 = 10. Agreguemos 10 a todos los números de cualquier cuadrado de 4x4 para obtener un cuadrado de 4x4 con un total de 74. Este cuadrado de 4x4 lo colocaremos como cuadrados de 2x2 en las 4 esquinas en el cuadro de 6x6 del lado izquierdo. Ahora tenemos números del 1 al 10 y del 27 al 36 para llenar los lugares vacíos.  3 Ahora primero completaremos las diagonales insertando 1 y 36, en una y 2 y 35, en la otra. El resto de los números están tan llenos que tenemos un total de 37 en el resto de los 2 lugares en filas y columnas con un total de 111 en cada una de la tercera y cuarta columnas y filas.
3 Ahora primero completaremos las diagonales insertando 1 y 36, en una y 2 y 35, en la otra. El resto de los números están tan llenos que tenemos un total de 37 en el resto de los 2 lugares en filas y columnas con un total de 111 en cada una de la tercera y cuarta columnas y filas.  4 El cuadrado completo de 6x6 sería como se muestra a continuación:
4 El cuadrado completo de 6x6 sería como se muestra a continuación:  5
5  6 Tenemos 880 cuadrados para elegir, además de colocar 3,4,6 y 10 tenemos 24 opciones. Esto se debe a que tenemos 4 opciones para colocar el primer número, 3 opciones para colocar el siguiente número y 2 opciones para el siguiente número. Del mismo modo, para colocar 5,7,8, y 9 tenemos 24 opciones, por lo que obtenemos fácilmente 880x24x24 todos los cuadrados diferentes. Además de las diagonales, tenemos la opción de elegir los números. En lugar de 1 y 2 podríamos haber elegido 9 y 10. Una combinación disponible sería 1,9,10, para una columna y 5,7,8 para la otra, y 3,4,10 para una fila y 2,6 , 9 para la otra fila. ¿Desarrollar otras combinaciones y cada una dará lugar a 880x24x24 nuevos cuadrados de 6x6?
6 Tenemos 880 cuadrados para elegir, además de colocar 3,4,6 y 10 tenemos 24 opciones. Esto se debe a que tenemos 4 opciones para colocar el primer número, 3 opciones para colocar el siguiente número y 2 opciones para el siguiente número. Del mismo modo, para colocar 5,7,8, y 9 tenemos 24 opciones, por lo que obtenemos fácilmente 880x24x24 todos los cuadrados diferentes. Además de las diagonales, tenemos la opción de elegir los números. En lugar de 1 y 2 podríamos haber elegido 9 y 10. Una combinación disponible sería 1,9,10, para una columna y 5,7,8 para la otra, y 3,4,10 para una fila y 2,6 , 9 para la otra fila. ¿Desarrollar otras combinaciones y cada una dará lugar a 880x24x24 nuevos cuadrados de 6x6?  7
7  8 Por supuesto, hay otros métodos para calcular los cuadrados de 6x6 y obtener más cuadrados de 6x6. Podríamos haber colocado el cuadrado 4x4 con un total de 74, como un cuadrado central y llenar los números del 1 al 10 y del 27 al 36 en los lugares vacíos en las casillas de las columnas 1st 2nd, 5th and 6th y 1st 2nd, 5th y 6ª filas. También hay otros métodos, intente poner el cuadrado 4x4 con un total de 74 en la 1ª a 4ª filas y columnas y llene las columnas 5ª y 6ª y las filas con los números disponibles. Pruebe otras formas también
8 Por supuesto, hay otros métodos para calcular los cuadrados de 6x6 y obtener más cuadrados de 6x6. Podríamos haber colocado el cuadrado 4x4 con un total de 74, como un cuadrado central y llenar los números del 1 al 10 y del 27 al 36 en los lugares vacíos en las casillas de las columnas 1st 2nd, 5th and 6th y 1st 2nd, 5th y 6ª filas. También hay otros métodos, intente poner el cuadrado 4x4 con un total de 74 en la 1ª a 4ª filas y columnas y llene las columnas 5ª y 6ª y las filas con los números disponibles. Pruebe otras formas también  9 Un cuadrado de pedido de 10x10 tendrá números del 1 al 100 con un total de 505. El cuadrado de orden 6x6 tenía números del 1 al 36. 100-36 = 64, 64/2 es 32. Entonces sumamos 32 a todos los números en el cuadrado de orden 6x6 para obtener uno con un total de 303. Esto se colocará en el centro y los espacios vacíos se llenarán primero con tres cuadrados de 4x4, un cuadrado tendrá números del 9 al 16 y 85 al 92, el segundo de 17 a 24 y 77 a 84 y el tercero de 25 a 32 y de 69 a 76. Ahora habrá Se deben llenar 16 espacios, 8 en las columnas 5, 6 y las filas 1, 2, 9 y 10, y 8 en las filas 5, 6 y las columnas 1, 2, 9 y 10. Tenemos que asegurarnos de que el conjunto de números son tales que en el primer caso las filas suman un total de 101 y en el segundo caso las columnas suman un total de 101, junto con asegurar que el total de la columna sea 202 en el 1er y el total de la fila sea 202 en el segundo caso. Si seleccionamos los números más pequeños con los mismos totales en las columnas y las filas, respectivamente, obtendremos los totales correctos. Es por esta razón que se han seleccionado 1 y 4, 2 y 3, 5 y 8 y 6 y 7.
9 Un cuadrado de pedido de 10x10 tendrá números del 1 al 100 con un total de 505. El cuadrado de orden 6x6 tenía números del 1 al 36. 100-36 = 64, 64/2 es 32. Entonces sumamos 32 a todos los números en el cuadrado de orden 6x6 para obtener uno con un total de 303. Esto se colocará en el centro y los espacios vacíos se llenarán primero con tres cuadrados de 4x4, un cuadrado tendrá números del 9 al 16 y 85 al 92, el segundo de 17 a 24 y 77 a 84 y el tercero de 25 a 32 y de 69 a 76. Ahora habrá Se deben llenar 16 espacios, 8 en las columnas 5, 6 y las filas 1, 2, 9 y 10, y 8 en las filas 5, 6 y las columnas 1, 2, 9 y 10. Tenemos que asegurarnos de que el conjunto de números son tales que en el primer caso las filas suman un total de 101 y en el segundo caso las columnas suman un total de 101, junto con asegurar que el total de la columna sea 202 en el 1er y el total de la fila sea 202 en el segundo caso. Si seleccionamos los números más pequeños con los mismos totales en las columnas y las filas, respectivamente, obtendremos los totales correctos. Es por esta razón que se han seleccionado 1 y 4, 2 y 3, 5 y 8 y 6 y 7.