Los números primos, una vez considerados una novedad matemática, han entrado en el prime time con el advenimiento de Internet y las modernas técnicas de encriptación. Al decidir si un número primo de 1024 dígitos puede ser computacionalmente difícil, usted mismo, con un poco de práctica, puede determinar la primalidad de cualquier número de 3 dígitos en su cabeza.
Y como todos los trucos mentales de la matemática, como los juegos malabares y el monociclo, es en esencia el arte de presumir. Ciertamente, leyendo esta explicación y practicando sus principios, su coordinación mente-ojo dará un salto adelante, pero, más importante aún, ¡podrá sorprender a sus amigos con su capacidad de cálculo!
Pasos
-
 1 Obtén lápiz y papel. Como cualquier principio matemático, lo recordarás mejor si practicas en papel al mismo tiempo.
1 Obtén lápiz y papel. Como cualquier principio matemático, lo recordarás mejor si practicas en papel al mismo tiempo. -
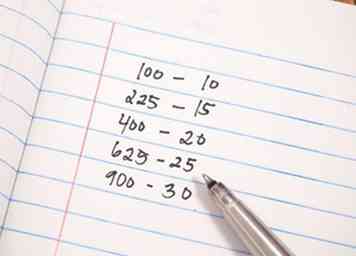 2 Estime la raíz cuadrada del número. Esto hará que su cheque sea más rápido ya que uno solo necesita intentar dividir el posible primo entre los números primos menores que la raíz cuadrada de ese número. Una referencia rápida podría ayudar: la raíz cuadrada de 100 es 10, de 225 es 15, de 400 es 20, de 625 es 25 y de 900 es 30.
2 Estime la raíz cuadrada del número. Esto hará que su cheque sea más rápido ya que uno solo necesita intentar dividir el posible primo entre los números primos menores que la raíz cuadrada de ese número. Una referencia rápida podría ayudar: la raíz cuadrada de 100 es 10, de 225 es 15, de 400 es 20, de 625 es 25 y de 900 es 30. -
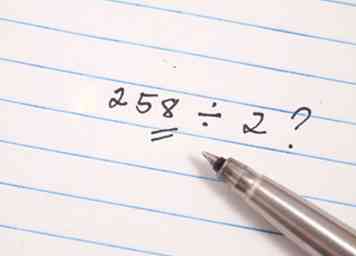 3 Aprenda a saber rápidamente si un número es divisible por 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 o 31. Dado que la raíz cuadrada de 1000 es aproximadamente 33, nunca necesitará probar ningún número mayor que 31. Al reducir el número de pruebas a 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, y 31, ya has ganado la mitad de la batalla.
3 Aprenda a saber rápidamente si un número es divisible por 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 o 31. Dado que la raíz cuadrada de 1000 es aproximadamente 33, nunca necesitará probar ningún número mayor que 31. Al reducir el número de pruebas a 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, y 31, ya has ganado la mitad de la batalla. - Estas son las reglas de divisibilidad para esos números primos:
- Divisible por 2 - Si el número termina en 2, 4, 6 u 8
- Divisible por 3 - Si los dígitos sumados son divisibles por 3
- Divisible por 5 - Si el número termina en 0 o 5
- Divisible por 7 - Tome el último dígito y multiplíquelo por dos. Reste ese número del resto de los dígitos. El número original es divisible por 7 si ese nuevo número es divisible por 7.
- Divisible por 11 - Tome el último dígito. Reste ese número del resto de los dígitos. El número original es divisible por 11 si ese nuevo número es divisible por 11.
- Divisible por 13 - Tome el último dígito y multiplíquelo por cuatro. Agrega ese número al resto de los dígitos. El número original es divisible por 13 si ese nuevo número es divisible por 13.
- Divisible por 17 - Tome el último dígito y multiplíquelo por cinco. Reste ese número del resto de los dígitos. El número original es divisible por 17 si ese nuevo número es divisible por 17. (Esto suena más difícil de lo que parece. Un ejemplo a continuación ilustrará).
- Divisible por 19 - Tome el último dígito y multiplíquelo por dos. Agrega ese número al resto de los dígitos. El número original es divisible por 19 si ese nuevo número es divisible por 19.
- Divisible por 23 - Tome el último dígito y multiplíquelo por siete. Agrega ese número al resto de los dígitos. El número original es divisible por 23 si ese nuevo número es divisible por 23.
- Divisible por 29 - Tome el último dígito y multiplíquelo por tres. Agrega ese número al resto de los dígitos. El número original es divisible por 29 si ese nuevo número es divisible por 29.
- Divisible por 31 - Tome el último dígito y multiplíquelo por tres. Reste ese número del resto de los dígitos. El número original es divisible por 31 si ese nuevo número es divisible por 31.
- Estas son las reglas de divisibilidad para esos números primos:
-
 4 Intenta dividir el posible primo entre los números primos menores que la raíz cuadrada de ese número.
4 Intenta dividir el posible primo entre los números primos menores que la raíz cuadrada de ese número. -
 5 Con una sonrisa de desprecio, proclama si es primordial y por qué es divisible.
5 Con una sonrisa de desprecio, proclama si es primordial y por qué es divisible. - Ejemplo Hagamos 781.
- Lápiz y papel. Comprobar.
- Estime la raíz cuadrada. 787 está entre 625 y 900, así que de la tabla de arriba, sé que la raíz cuadrada de 787 estará entre 25 y 30, probablemente alrededor de 27. Entonces, los números primos que necesitaré para probar son 2, 3, 5, 7, 11, 13, 17, 19 y 23. El próximo primo es 29, y mi matemática mental me dice que la raíz cuadrada de 787 probablemente no sea 29 porque no está muy cerca de 900.
- Compruebe la divisibilidad en 2, 3, 5, 7, 11, 13, 17, 19 y 23.
- Por dos: 781 no termina en 2, 4, 6 u 8. Hasta ahora todo bien.
- Por tres: Agrega los dígitos; 7 + 8 + 1 = 16. 16 no es divisible por 3, entonces tampoco lo es 781.
- Para las cinco: 781 no termina en 0 o 5. Todavía primo.
- Para las siete: Multiplica el último dígito por dos; 1 * 2 = 2. Restarlo de los dígitos restantes; 78 - 2 = 76. 76 no es divisible por 7 (recuerde que 70 es y 77 es), tampoco lo es 781.
- A las once: Reste el último dígito de los dígitos restantes; 78 - 1 = 77. 77 es divisible por 11, por lo que 781 también lo es.
- Entonces, 781 no es primo. Es al menos divisible por 11.
- Ejemplo n. ° 2 Hagamos 527.
- Lápiz y papel. Comprobar.
- Estime la raíz cuadrada. 527 está entre 400 y 625. Por lo tanto, mirando mi tabla, la raíz cuadrada de 527 es probablemente alrededor de 23. Entonces, los números primos que necesitaré para probar son 2 a 23, nuevamente.
- Compruebe la divisibilidad en 2, 3, 5, 7, 11, 13, 17, 19 y 23.
- Por dos: 527 no termina en 2, 4, 6 u 8. Hasta ahora todo bien.
- Por tres: Agrega los dígitos; 5 + 2 + 7 = 14. 14 no es divisible por 3, por lo que tampoco es 527.
- Para las cinco: 527 no termina en 0 o 5. Avanzando.
- Para las siete: Multiplica el último dígito por dos; 2 * 7 = 14. Restarlo de los dígitos restantes; 52 - 14 = 38. 38 no es divisible por 7, por lo que tampoco es 527.
- A las once: Reste el último dígito de los dígitos restantes; 52 - 7 = 45. 45 no es divisible por 11, por lo que tampoco es 527.
- Por trece: Multiplique el último dígito por cuatro; 7 * 4 = 28. Agregue también los dígitos restantes; 52 + 28 = 80. 80 no es divisible por 13, por lo que tampoco es 527.
- A los diecisiete años: Multiplique el último dígito por cinco; 7 * 5 = 35. Restarlo de los dígitos restantes; 52 - 35 = 17. 17 es divisible por 17, por lo que 527 es demasiado.
- Entonces, 527 no es primo. Es al menos divisible por 17.
- Ejemplo Hagamos 781.
 Minotauromaquia
Minotauromaquia
 1 Obtén lápiz y papel. Como cualquier principio matemático, lo recordarás mejor si practicas en papel al mismo tiempo.
1 Obtén lápiz y papel. Como cualquier principio matemático, lo recordarás mejor si practicas en papel al mismo tiempo. 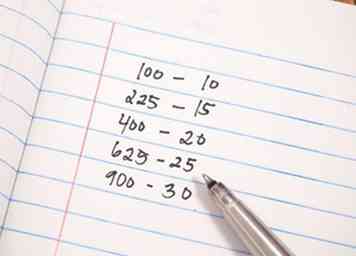 2 Estime la raíz cuadrada del número. Esto hará que su cheque sea más rápido ya que uno solo necesita intentar dividir el posible primo entre los números primos menores que la raíz cuadrada de ese número. Una referencia rápida podría ayudar: la raíz cuadrada de 100 es 10, de 225 es 15, de 400 es 20, de 625 es 25 y de 900 es 30.
2 Estime la raíz cuadrada del número. Esto hará que su cheque sea más rápido ya que uno solo necesita intentar dividir el posible primo entre los números primos menores que la raíz cuadrada de ese número. Una referencia rápida podría ayudar: la raíz cuadrada de 100 es 10, de 225 es 15, de 400 es 20, de 625 es 25 y de 900 es 30. 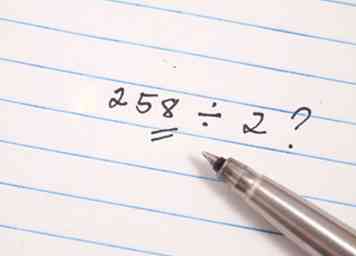 3 Aprenda a saber rápidamente si un número es divisible por 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 o 31. Dado que la raíz cuadrada de 1000 es aproximadamente 33, nunca necesitará probar ningún número mayor que 31. Al reducir el número de pruebas a 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, y 31, ya has ganado la mitad de la batalla.
3 Aprenda a saber rápidamente si un número es divisible por 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 o 31. Dado que la raíz cuadrada de 1000 es aproximadamente 33, nunca necesitará probar ningún número mayor que 31. Al reducir el número de pruebas a 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, y 31, ya has ganado la mitad de la batalla.  4 Intenta dividir el posible primo entre los números primos menores que la raíz cuadrada de ese número.
4 Intenta dividir el posible primo entre los números primos menores que la raíz cuadrada de ese número.  5 Con una sonrisa de desprecio, proclama si es primordial y por qué es divisible.
5 Con una sonrisa de desprecio, proclama si es primordial y por qué es divisible.