Euclides, en su famoso tratado de 13 libros sobre Geometría, "Elementos", da en el Libro I la Proposición 2, la Solución y Demostración de cómo "Desde un punto dado (A) dibujar una línea derecha igual a una línea derecha finita dada (BC ) ". Este artículo le mostrará cómo logró la solución y la demostración, y así la prueba del problema. Además, demostrará el uso de la opción de herramienta "Shapes" del navegador multimedia de Excel, empleada para simular una prueba geométrica.
Parte uno de tres:
El tutorial
-

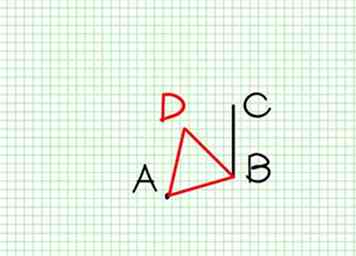
 1
1
Solución --- Únete a AB (Post.I.); en AB describa el triángulo equilátero ABD [I.1] - (consulte el artículo Cómo determinar una línea = a raíz cuadrada de 3 geométricamente, sobre cómo construir un triángulo equilátero correctamente si no sabe cómo). Para hacer esto usando el Explorador de medios, siga los pasos secundarios dentro de estas imágenes tomadas de Excel y convertidas a través de la aplicación Vista previa a archivos png. -
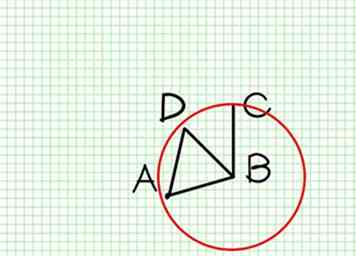 2 Con B como centro y BC como radio, describe el círculo ECH (Post. III.).
2 Con B como centro y BC como radio, describe el círculo ECH (Post. III.). -
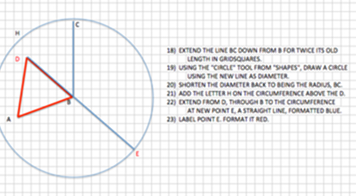
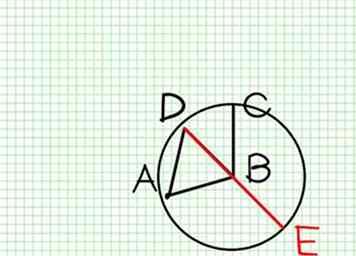 3 Produce DB para cumplir con el círculo ECH en E (Post. II).
3 Produce DB para cumplir con el círculo ECH en E (Post. II). -

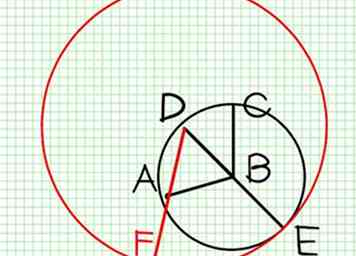 4 Con D como centro y DE como radio, describe el círculo EFG (Publicación. III.). Produce DA para cumplir con este círculo en AF.
4 Con D como centro y DE como radio, describe el círculo EFG (Publicación. III.). Produce DA para cumplir con este círculo en AF. -
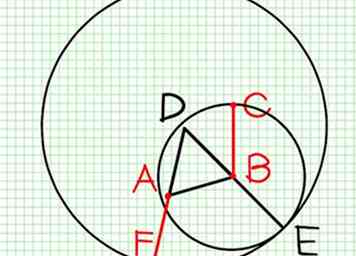 5 Tenga en cuenta que AF es igual a BC.
5 Tenga en cuenta que AF es igual a BC. -
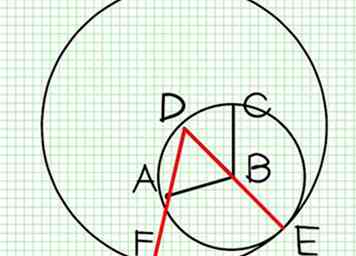 6 Demostrar --- Porque D es el centro del círculo EFG, DF es igual a DE (Def. XXXII.).
6 Demostrar --- Porque D es el centro del círculo EFG, DF es igual a DE (Def. XXXII.).
Parte dos de tres:
Gráficos Explicativos, Diagramas, Fotos
-
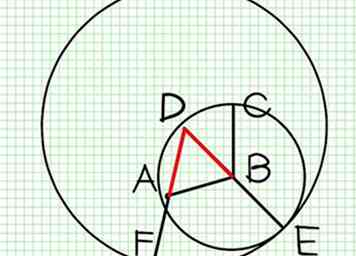 1 Como DAB es un triángulo equilátero, sepa que DA es igual a DB (Def. XXI.). Por lo tanto, tenemos DF = DE, y DA = DB; y tomando lo último de lo primero, el resto AF es igual al resto BE (Axioma III). De nuevo, porque B es el centro del círculo ECH, BC es igual a BE; y [se demuestra] que AF es igual a BE; y las cosas que son iguales a la misma cosa son iguales entre sí (Axioma I)
1 Como DAB es un triángulo equilátero, sepa que DA es igual a DB (Def. XXI.). Por lo tanto, tenemos DF = DE, y DA = DB; y tomando lo último de lo primero, el resto AF es igual al resto BE (Axioma III). De nuevo, porque B es el centro del círculo ECH, BC es igual a BE; y [se demuestra] que AF es igual a BE; y las cosas que son iguales a la misma cosa son iguales entre sí (Axioma I) -
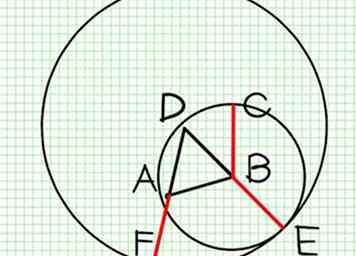 2 Por lo tanto, AF es igual a BC. Por lo tanto, desde el punto A dado, la línea AF se ha dibujado igual a la línea BC.
2 Por lo tanto, AF es igual a BC. Por lo tanto, desde el punto A dado, la línea AF se ha dibujado igual a la línea BC. -
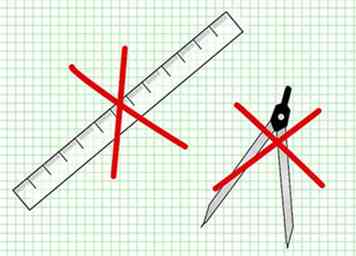 3 Es habitual que los comentaristas de Euclides digan que permite el uso de la regla y la brújula. Si tal fuera el caso, esta Proposición habría sido innecesaria. El hecho es que el objetivo de Euclides era enseñar Geometría Teórica y no Práctica, y las únicas cosas que postula son el trazado de líneas rectas y la descripción de círculos. Si permitiera el uso mecánico de la regla y la brújula, podría dar métodos para resolver muchos problemas que van más allá de los límites de "geometría del punto, línea y círculo". Ver Notas D, F al final de este trabajo (en referencia a Archives.org o la publicación de The Royal University of Ireland) .
3 Es habitual que los comentaristas de Euclides digan que permite el uso de la regla y la brújula. Si tal fuera el caso, esta Proposición habría sido innecesaria. El hecho es que el objetivo de Euclides era enseñar Geometría Teórica y no Práctica, y las únicas cosas que postula son el trazado de líneas rectas y la descripción de círculos. Si permitiera el uso mecánico de la regla y la brújula, podría dar métodos para resolver muchos problemas que van más allá de los límites de "geometría del punto, línea y círculo". Ver Notas D, F al final de este trabajo (en referencia a Archives.org o la publicación de The Royal University of Ireland) .
Parte tres de tres:
Orientación útil
- 1 Haga uso de artículos auxiliares cuando proceda a través de este tutorial:
- Para obtener una lista de artículos relacionados con Excel, arte geométrico y / o trigonométrico, gráficos / diagramas y formulación algebraica, vea el artículo Cómo crear una ruta de partículas espirales o una forma de collar o borde esférico.
- Para obtener gráficos y gráficos más artísticos, también puede hacer clic en Categoría: Imágenes de Microsoft Excel, Categoría: Matemáticas, Categoría: Hojas de cálculo o Categoría: Gráficos para ver muchas hojas de cálculo y tablas de Excel donde Trigonometría, Geometría y Cálculo se han convertido en Arte. o simplemente haga clic en la categoría que aparece en la parte superior derecha blanca de esta página, o en la parte inferior izquierda de la página.
 Minotauromaquia
Minotauromaquia

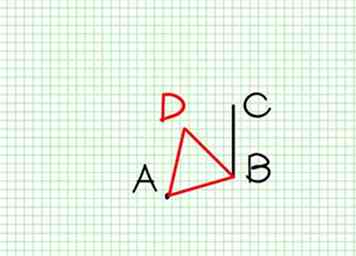
 1
1  2 Con B como centro y BC como radio, describe el círculo ECH (Post. III.).
2 Con B como centro y BC como radio, describe el círculo ECH (Post. III.). 
 3 Produce DB para cumplir con el círculo ECH en E (Post. II).
3 Produce DB para cumplir con el círculo ECH en E (Post. II). 
 4 Con D como centro y DE como radio, describe el círculo EFG (Publicación. III.). Produce DA para cumplir con este círculo en AF.
4 Con D como centro y DE como radio, describe el círculo EFG (Publicación. III.). Produce DA para cumplir con este círculo en AF.  5 Tenga en cuenta que AF es igual a BC.
5 Tenga en cuenta que AF es igual a BC.  6 Demostrar --- Porque D es el centro del círculo EFG, DF es igual a DE (Def. XXXII.).
6 Demostrar --- Porque D es el centro del círculo EFG, DF es igual a DE (Def. XXXII.).  1 Como DAB es un triángulo equilátero, sepa que DA es igual a DB (Def. XXI.). Por lo tanto, tenemos DF = DE, y DA = DB; y tomando lo último de lo primero, el resto AF es igual al resto BE (Axioma III). De nuevo, porque B es el centro del círculo ECH, BC es igual a BE; y [se demuestra] que AF es igual a BE; y las cosas que son iguales a la misma cosa son iguales entre sí (Axioma I)
1 Como DAB es un triángulo equilátero, sepa que DA es igual a DB (Def. XXI.). Por lo tanto, tenemos DF = DE, y DA = DB; y tomando lo último de lo primero, el resto AF es igual al resto BE (Axioma III). De nuevo, porque B es el centro del círculo ECH, BC es igual a BE; y [se demuestra] que AF es igual a BE; y las cosas que son iguales a la misma cosa son iguales entre sí (Axioma I)  2 Por lo tanto, AF es igual a BC. Por lo tanto, desde el punto A dado, la línea AF se ha dibujado igual a la línea BC.
2 Por lo tanto, AF es igual a BC. Por lo tanto, desde el punto A dado, la línea AF se ha dibujado igual a la línea BC.  3 Es habitual que los comentaristas de Euclides digan que permite el uso de la regla y la brújula. Si tal fuera el caso, esta Proposición habría sido innecesaria. El hecho es que el objetivo de Euclides era enseñar Geometría Teórica y no Práctica, y las únicas cosas que postula son el trazado de líneas rectas y la descripción de círculos. Si permitiera el uso mecánico de la regla y la brújula, podría dar métodos para resolver muchos problemas que van más allá de los límites de "geometría del punto, línea y círculo". Ver Notas D, F al final de este trabajo (en referencia a Archives.org o la publicación de The Royal University of Ireland) .
3 Es habitual que los comentaristas de Euclides digan que permite el uso de la regla y la brújula. Si tal fuera el caso, esta Proposición habría sido innecesaria. El hecho es que el objetivo de Euclides era enseñar Geometría Teórica y no Práctica, y las únicas cosas que postula son el trazado de líneas rectas y la descripción de círculos. Si permitiera el uso mecánico de la regla y la brújula, podría dar métodos para resolver muchos problemas que van más allá de los límites de "geometría del punto, línea y círculo". Ver Notas D, F al final de este trabajo (en referencia a Archives.org o la publicación de The Royal University of Ireland) .