La prueba de hipótesis está guiada por análisis estadísticos. La significancia estadística se calcula utilizando un valor p, que le indica la probabilidad de que se observe su resultado, dado que una determinada afirmación (la hipótesis nula) es verdadera.[1] Si este valor p es menor que el nivel de significancia establecido (generalmente 0.05), el experimentador puede asumir que la hipótesis nula es falsa y aceptar la hipótesis alternativa. Usando una prueba t simple, puede calcular un valor p y determinar la significancia entre dos grupos diferentes de un conjunto de datos.
Parte uno de tres:
Configurando tu experimento
-
 1 Define tus hipótesis El primer paso para evaluar la significación estadística es definir la pregunta que desea responder y establecer su hipótesis. La hipótesis es una declaración sobre sus datos experimentales y las diferencias que pueden estar ocurriendo en la población. Para cualquier experimento, hay una hipótesis nula y otra alternativa.[2] Generalmente, comparará dos grupos para ver si son iguales o diferentes.
1 Define tus hipótesis El primer paso para evaluar la significación estadística es definir la pregunta que desea responder y establecer su hipótesis. La hipótesis es una declaración sobre sus datos experimentales y las diferencias que pueden estar ocurriendo en la población. Para cualquier experimento, hay una hipótesis nula y otra alternativa.[2] Generalmente, comparará dos grupos para ver si son iguales o diferentes. - La hipótesis nula (H0) generalmente establece que no hay diferencia entre sus dos conjuntos de datos. Por ejemplo: los estudiantes que leen el material antes de la clase no obtienen mejores calificaciones finales.
- La hipótesis alternativa (Hun) es lo opuesto a la hipótesis nula y es la afirmación que intentas respaldar con tus datos experimentales. Por ejemplo: los estudiantes que leen el material antes de clase obtienen mejores notas finales.
-
 2 Establezca el nivel de significancia para determinar cuán inusual debe ser su información antes de que pueda considerarse significativa. El nivel de significancia (también llamado alfa) es el umbral que establece para determinar la importancia. Si su valor p es menor o igual que el nivel de significancia establecido, los datos se consideran estadísticamente significativos.[3]
2 Establezca el nivel de significancia para determinar cuán inusual debe ser su información antes de que pueda considerarse significativa. El nivel de significancia (también llamado alfa) es el umbral que establece para determinar la importancia. Si su valor p es menor o igual que el nivel de significancia establecido, los datos se consideran estadísticamente significativos.[3] - Como regla general, el nivel de significancia (o alfa) comúnmente se establece en 0.05, lo que significa que la probabilidad de observar las diferencias observadas en sus datos por casualidad es solo del 5%.
- Un nivel de confianza más alto (y, por lo tanto, un valor p más bajo) significa que los resultados son más significativos.
- Si desea una mayor confianza en sus datos, establezca el p-valor más bajo en 0.01. Los valores p más bajos generalmente se usan en la fabricación cuando se detectan defectos en los productos. Es muy importante tener una gran confianza en que cada pieza funcionará exactamente como se supone que debe hacerlo.
- Para la mayoría de los experimentos impulsados por hipótesis, un nivel de significancia de 0.05 es aceptable.
-
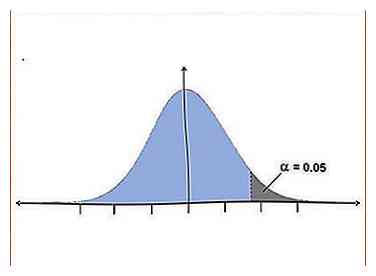 3 Decida usar una prueba de una cola o dos colas. Una de las suposiciones que hace una prueba t es que sus datos se distribuyen normalmente. Una distribución normal de datos forma una curva de campana con la mayoría de las muestras cayendo en el medio.[4] La prueba t es una prueba matemática para ver si sus datos quedan fuera de la distribución normal, ya sea arriba o abajo, en las "colas" de la curva.
3 Decida usar una prueba de una cola o dos colas. Una de las suposiciones que hace una prueba t es que sus datos se distribuyen normalmente. Una distribución normal de datos forma una curva de campana con la mayoría de las muestras cayendo en el medio.[4] La prueba t es una prueba matemática para ver si sus datos quedan fuera de la distribución normal, ya sea arriba o abajo, en las "colas" de la curva. - Una prueba de una cola es más poderosa que una prueba de dos colas, ya que examina el potencial de una relación en una sola dirección (como por encima del grupo de control), mientras que una prueba de dos colas examina el potencial de una relación en ambos direcciones (como arriba o abajo del grupo de control).[5]
- Si no está seguro de si sus datos estarán por encima o por debajo del grupo de control, use una prueba de dos colas. Esto le permite probar la significancia en cualquier dirección.
- Si sabe en qué dirección está esperando que avance su información, use una prueba de una cola. En el ejemplo dado, usted espera que las calificaciones del alumno mejoren; por lo tanto, usará una prueba de una cola.
-
 4 Determine el tamaño de muestra con un análisis de potencia. El poder de una prueba es la probabilidad de observar el resultado esperado, dado un tamaño de muestra específico.[6] El umbral común para el poder (o β) es del 80%. Un análisis de potencia puede ser un poco complicado sin algunos datos preliminares, ya que necesita información sobre los medios esperados entre cada grupo y sus desviaciones estándar. Use una calculadora de análisis de energía en línea para determinar el tamaño de muestra óptimo para sus datos.[7]
4 Determine el tamaño de muestra con un análisis de potencia. El poder de una prueba es la probabilidad de observar el resultado esperado, dado un tamaño de muestra específico.[6] El umbral común para el poder (o β) es del 80%. Un análisis de potencia puede ser un poco complicado sin algunos datos preliminares, ya que necesita información sobre los medios esperados entre cada grupo y sus desviaciones estándar. Use una calculadora de análisis de energía en línea para determinar el tamaño de muestra óptimo para sus datos.[7] - Los investigadores generalmente hacen un pequeño estudio piloto para informar su análisis de poder y determinar el tamaño de muestra necesario para un estudio más amplio y completo.
- Si no tiene los medios para realizar un estudio piloto complejo, haga algunas estimaciones sobre los posibles medios basados en la lectura de la literatura y los estudios que otros individuos pudieron haber realizado. Esto le dará un buen lugar para comenzar con el tamaño de la muestra.
Parte dos de tres:
Cálculo de la desviación estándar
-
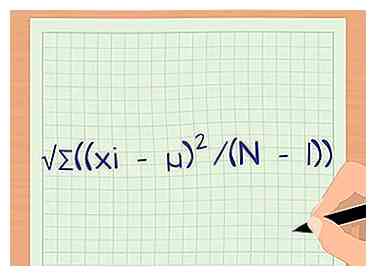 1 Defina la fórmula para la desviación estándar. La desviación estándar es una medida de la dispersión de sus datos. Le brinda información sobre cuán similar es cada punto de datos dentro de su muestra, lo que le ayuda a determinar si los datos son significativos. A primera vista, la ecuación puede parecer un poco complicada, pero estos pasos lo guiarán a través del proceso del cálculo. La fórmula es s = √Σ ((xyo - µ)2/ (N - 1)).
1 Defina la fórmula para la desviación estándar. La desviación estándar es una medida de la dispersión de sus datos. Le brinda información sobre cuán similar es cada punto de datos dentro de su muestra, lo que le ayuda a determinar si los datos son significativos. A primera vista, la ecuación puede parecer un poco complicada, pero estos pasos lo guiarán a través del proceso del cálculo. La fórmula es s = √Σ ((xyo - µ)2/ (N - 1)). - s es la desviación estándar.
- Σ indica que sumará todos los valores de muestra recopilados.
- Xyo representa cada valor individual de sus datos.
- μ es el promedio (o media) de sus datos para cada grupo.
- N es el número de muestra total.
-
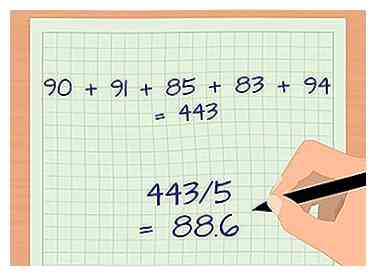 2 Promedio de las muestras en cada grupo. Para calcular la desviación estándar, primero debe tomar el promedio de las muestras en los grupos individuales. El promedio se designa con la letra griega mu o μ. Para hacer esto, simplemente agregue cada muestra y luego divida por el número total de muestras.[8]
2 Promedio de las muestras en cada grupo. Para calcular la desviación estándar, primero debe tomar el promedio de las muestras en los grupos individuales. El promedio se designa con la letra griega mu o μ. Para hacer esto, simplemente agregue cada muestra y luego divida por el número total de muestras.[8] - Por ejemplo, para encontrar la calificación promedio del grupo que lee el material antes de la clase, veamos algunos datos. Para simplificar, utilizaremos un conjunto de datos de 5 puntos: 90, 91, 85, 83 y 94.
- Agregue todas las muestras juntas: 90 + 91 + 85 + 83 + 94 = 443.
- Divida la suma por el número de muestra, N = 5: 443/5 = 88.6.
- La calificación promedio para este grupo es 88.6.
-
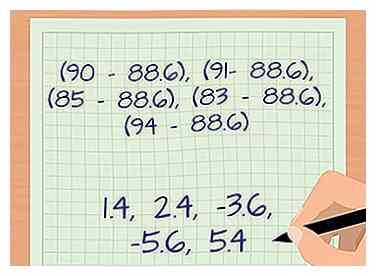 3 Reste cada muestra del promedio. La siguiente parte del cálculo implica el (xyo - μ) porción de la ecuación. Usted restará cada muestra del promedio recién calculado. Para nuestro ejemplo, terminarás con cinco restas.
3 Reste cada muestra del promedio. La siguiente parte del cálculo implica el (xyo - μ) porción de la ecuación. Usted restará cada muestra del promedio recién calculado. Para nuestro ejemplo, terminarás con cinco restas. - (90 - 88.6), (91 - 88.6), (85 - 88.6), (83 - 88.6) y (94 - 88.6).
- Los números calculados ahora son 1.4, 2.4, -3.6, -5.6 y 5.4.
-
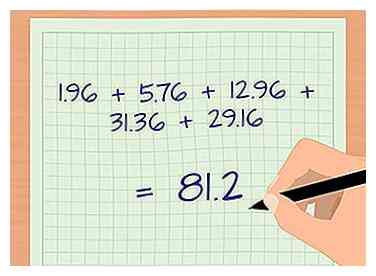 4 Cuadre cada uno de estos números y agréguelos. Cada uno de los nuevos números que acaba de calcular se cuadrará. Este paso también se ocupará de los signos negativos. Si tiene un signo negativo después de este paso o al final de su cálculo, es posible que haya olvidado este paso.
4 Cuadre cada uno de estos números y agréguelos. Cada uno de los nuevos números que acaba de calcular se cuadrará. Este paso también se ocupará de los signos negativos. Si tiene un signo negativo después de este paso o al final de su cálculo, es posible que haya olvidado este paso. - En nuestro ejemplo, ahora estamos trabajando con 1.96, 5.76, 12.96, 31.36 y 29.16.
- Sumando estos cuadrados juntos produce: 1.96 + 5.76 + 12.96 + 31.36 + 29.16 = 81.2.
-
 5 Divida por el número de muestra total menos 1. La fórmula se divide por N - 1 porque está corrigiendo el hecho de que no ha contado a toda una población; está tomando una muestra de la población de todos los estudiantes para hacer una estimación.[9]
5 Divida por el número de muestra total menos 1. La fórmula se divide por N - 1 porque está corrigiendo el hecho de que no ha contado a toda una población; está tomando una muestra de la población de todos los estudiantes para hacer una estimación.[9] - Restar: N - 1 = 5 - 1 = 4
- Divide: 81.2 / 4 = 20.3
-
 6 Toma la raíz cuadrada. Una vez que haya dividido por el número de muestra menos uno, tome la raíz cuadrada de este número final. Este es el último paso para calcular la desviación estándar. Hay programas estadísticos que harán este cálculo por usted después de ingresar los datos brutos.
6 Toma la raíz cuadrada. Una vez que haya dividido por el número de muestra menos uno, tome la raíz cuadrada de este número final. Este es el último paso para calcular la desviación estándar. Hay programas estadísticos que harán este cálculo por usted después de ingresar los datos brutos. - Para nuestro ejemplo, la desviación estándar de las calificaciones finales de los estudiantes que leen antes de la clase es: s = √20.3 = 4.51.
Parte tres de tres:
Determinar la importancia
-
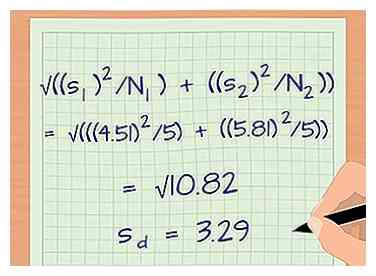 1 Calcule la varianza entre sus 2 grupos de muestra. Hasta este punto, el ejemplo solo ha tratado con 1 de los grupos de muestra. Si está intentando comparar 2 grupos, obviamente tendrá datos de ambos. Calcule la desviación estándar del segundo grupo de muestras y utilícela para calcular la varianza entre los 2 grupos experimentales. La fórmula para la varianza es sre = √ ((s1/NORTE1) + (s)2/NORTE2)).[10]
1 Calcule la varianza entre sus 2 grupos de muestra. Hasta este punto, el ejemplo solo ha tratado con 1 de los grupos de muestra. Si está intentando comparar 2 grupos, obviamente tendrá datos de ambos. Calcule la desviación estándar del segundo grupo de muestras y utilícela para calcular la varianza entre los 2 grupos experimentales. La fórmula para la varianza es sre = √ ((s1/NORTE1) + (s)2/NORTE2)).[10] - sre es la varianza entre tus grupos
- s1 es la desviación estándar del grupo 1 y N1 es el tamaño de muestra del grupo 1.
- s2 es la desviación estándar del grupo 2 y N2 es el tamaño de muestra del grupo 2.
- Para nuestro ejemplo, digamos que los datos del grupo 2 (estudiantes que no leyeron antes de la clase) tenían un tamaño de muestra de 5 y una desviación estándar de 5.81. La varianza es:
- sre = √ ((s1)2/NORTE1) + ((s2)2/NORTE2))
- sre = √(((4.51)2/5) + ((5.81)2/5)) = √((20.34/5) + (33.76/5)) = √(4.07 + 6.75) = √10.82 = 3.29.
-
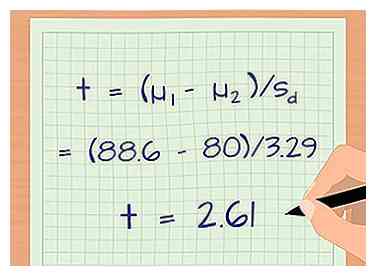 2 Calcule el puntaje t de sus datos. Un puntaje t le permite convertir sus datos en una forma que le permite compararlos con otros datos. Los puntajes T le permiten realizar una prueba t que le permite calcular la probabilidad de que dos grupos sean significativamente diferentes entre sí. La fórmula para un puntaje t es: t = (μ1 - µ2) / sre.[11]
2 Calcule el puntaje t de sus datos. Un puntaje t le permite convertir sus datos en una forma que le permite compararlos con otros datos. Los puntajes T le permiten realizar una prueba t que le permite calcular la probabilidad de que dos grupos sean significativamente diferentes entre sí. La fórmula para un puntaje t es: t = (μ1 - µ2) / sre.[11] - µ1 es el promedio del primer grupo.
- µ2 es el promedio del segundo grupo.
- sre es la varianza entre tus muestras
- Use el promedio más grande como μ1 por lo que no tendrá un valor t negativo.
- Para nuestro ejemplo, digamos que el promedio de muestra para el grupo 2 (los que no leyeron) fue 80. El puntaje t es: t = (μ1 - µ2) / sre = (88.6 - 80)/3.29 = 2.61.
-
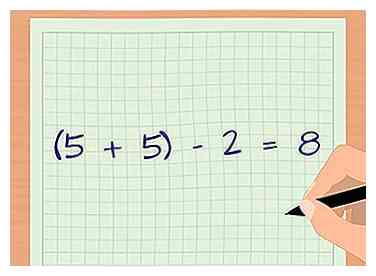 3 Determine los grados de libertad de su muestra. Al usar el puntaje t, el número de grados de libertad se determina usando el tamaño de muestra. Sume la cantidad de muestras de cada grupo y luego reste dos. Para nuestro ejemplo, los grados de libertad (d.f.) son 8 porque hay cinco muestras en el primer grupo y cinco muestras en el segundo grupo ((5 + 5) - 2 = 8).[12]
3 Determine los grados de libertad de su muestra. Al usar el puntaje t, el número de grados de libertad se determina usando el tamaño de muestra. Sume la cantidad de muestras de cada grupo y luego reste dos. Para nuestro ejemplo, los grados de libertad (d.f.) son 8 porque hay cinco muestras en el primer grupo y cinco muestras en el segundo grupo ((5 + 5) - 2 = 8).[12] -
 4 Use una tabla t para evaluar la significancia. Una tabla de puntajes t[13] y los grados de libertad se pueden encontrar en un libro de estadísticas estándar o en línea. Mire la fila que contiene los grados de libertad para sus datos y encuentre el valor p que corresponde a su puntaje t.
4 Use una tabla t para evaluar la significancia. Una tabla de puntajes t[13] y los grados de libertad se pueden encontrar en un libro de estadísticas estándar o en línea. Mire la fila que contiene los grados de libertad para sus datos y encuentre el valor p que corresponde a su puntaje t. - Con 8 d.f. y un puntaje t de 2.61, el valor de p para una prueba de una cola cae entre 0.01 y 0.025. Debido a que establecemos nuestro nivel de significancia menor o igual a 0.05, nuestros datos son estadísticamente significativos. Con estos datos, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa:[14] los estudiantes que leen el material antes de clase obtienen mejores calificaciones finales.
-
 5 Considera un estudio de seguimiento. Muchos investigadores hacen un pequeño estudio piloto con algunas medidas para ayudarlos a entender cómo diseñar un estudio más amplio. Hacer otro estudio, con más mediciones, ayudará a aumentar su confianza sobre su conclusión.
5 Considera un estudio de seguimiento. Muchos investigadores hacen un pequeño estudio piloto con algunas medidas para ayudarlos a entender cómo diseñar un estudio más amplio. Hacer otro estudio, con más mediciones, ayudará a aumentar su confianza sobre su conclusión. - Un estudio de seguimiento puede ayudarlo a determinar si alguna de sus conclusiones contuvo un error tipo I (observar una diferencia cuando no hay una, o un falso rechazo de la hipótesis nula) o un error tipo II (no observar una diferencia cuando hay una uno, o falsa aceptación de la hipótesis nula).[15]
 Minotauromaquia
Minotauromaquia
 1 Define tus hipótesis El primer paso para evaluar la significación estadística es definir la pregunta que desea responder y establecer su hipótesis. La hipótesis es una declaración sobre sus datos experimentales y las diferencias que pueden estar ocurriendo en la población. Para cualquier experimento, hay una hipótesis nula y otra alternativa.[2] Generalmente, comparará dos grupos para ver si son iguales o diferentes.
1 Define tus hipótesis El primer paso para evaluar la significación estadística es definir la pregunta que desea responder y establecer su hipótesis. La hipótesis es una declaración sobre sus datos experimentales y las diferencias que pueden estar ocurriendo en la población. Para cualquier experimento, hay una hipótesis nula y otra alternativa.[2] Generalmente, comparará dos grupos para ver si son iguales o diferentes.  2 Establezca el nivel de significancia para determinar cuán inusual debe ser su información antes de que pueda considerarse significativa. El nivel de significancia (también llamado alfa) es el umbral que establece para determinar la importancia. Si su valor p es menor o igual que el nivel de significancia establecido, los datos se consideran estadísticamente significativos.[3]
2 Establezca el nivel de significancia para determinar cuán inusual debe ser su información antes de que pueda considerarse significativa. El nivel de significancia (también llamado alfa) es el umbral que establece para determinar la importancia. Si su valor p es menor o igual que el nivel de significancia establecido, los datos se consideran estadísticamente significativos.[3]  3 Decida usar una prueba de una cola o dos colas. Una de las suposiciones que hace una prueba t es que sus datos se distribuyen normalmente. Una distribución normal de datos forma una curva de campana con la mayoría de las muestras cayendo en el medio.[4] La prueba t es una prueba matemática para ver si sus datos quedan fuera de la distribución normal, ya sea arriba o abajo, en las "colas" de la curva.
3 Decida usar una prueba de una cola o dos colas. Una de las suposiciones que hace una prueba t es que sus datos se distribuyen normalmente. Una distribución normal de datos forma una curva de campana con la mayoría de las muestras cayendo en el medio.[4] La prueba t es una prueba matemática para ver si sus datos quedan fuera de la distribución normal, ya sea arriba o abajo, en las "colas" de la curva.  4 Determine el tamaño de muestra con un análisis de potencia. El poder de una prueba es la probabilidad de observar el resultado esperado, dado un tamaño de muestra específico.[6] El umbral común para el poder (o β) es del 80%. Un análisis de potencia puede ser un poco complicado sin algunos datos preliminares, ya que necesita información sobre los medios esperados entre cada grupo y sus desviaciones estándar. Use una calculadora de análisis de energía en línea para determinar el tamaño de muestra óptimo para sus datos.[7]
4 Determine el tamaño de muestra con un análisis de potencia. El poder de una prueba es la probabilidad de observar el resultado esperado, dado un tamaño de muestra específico.[6] El umbral común para el poder (o β) es del 80%. Un análisis de potencia puede ser un poco complicado sin algunos datos preliminares, ya que necesita información sobre los medios esperados entre cada grupo y sus desviaciones estándar. Use una calculadora de análisis de energía en línea para determinar el tamaño de muestra óptimo para sus datos.[7] 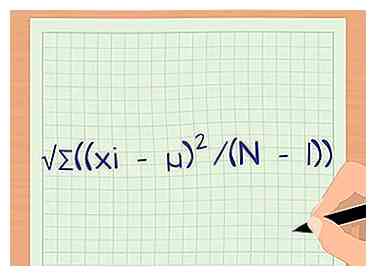 1 Defina la fórmula para la desviación estándar. La desviación estándar es una medida de la dispersión de sus datos. Le brinda información sobre cuán similar es cada punto de datos dentro de su muestra, lo que le ayuda a determinar si los datos son significativos. A primera vista, la ecuación puede parecer un poco complicada, pero estos pasos lo guiarán a través del proceso del cálculo. La fórmula es s = √Σ ((xyo - µ)2/ (N - 1)).
1 Defina la fórmula para la desviación estándar. La desviación estándar es una medida de la dispersión de sus datos. Le brinda información sobre cuán similar es cada punto de datos dentro de su muestra, lo que le ayuda a determinar si los datos son significativos. A primera vista, la ecuación puede parecer un poco complicada, pero estos pasos lo guiarán a través del proceso del cálculo. La fórmula es s = √Σ ((xyo - µ)2/ (N - 1)). 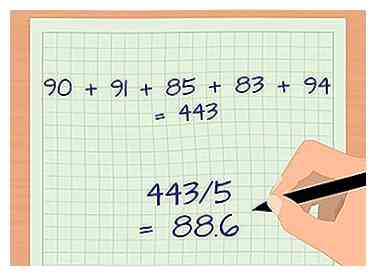 2 Promedio de las muestras en cada grupo. Para calcular la desviación estándar, primero debe tomar el promedio de las muestras en los grupos individuales. El promedio se designa con la letra griega mu o μ. Para hacer esto, simplemente agregue cada muestra y luego divida por el número total de muestras.[8]
2 Promedio de las muestras en cada grupo. Para calcular la desviación estándar, primero debe tomar el promedio de las muestras en los grupos individuales. El promedio se designa con la letra griega mu o μ. Para hacer esto, simplemente agregue cada muestra y luego divida por el número total de muestras.[8] 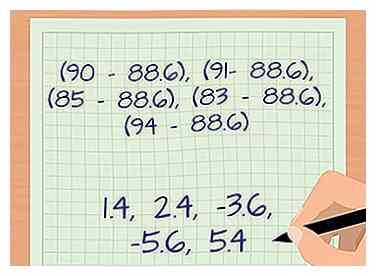 3 Reste cada muestra del promedio. La siguiente parte del cálculo implica el (xyo - μ) porción de la ecuación. Usted restará cada muestra del promedio recién calculado. Para nuestro ejemplo, terminarás con cinco restas.
3 Reste cada muestra del promedio. La siguiente parte del cálculo implica el (xyo - μ) porción de la ecuación. Usted restará cada muestra del promedio recién calculado. Para nuestro ejemplo, terminarás con cinco restas. 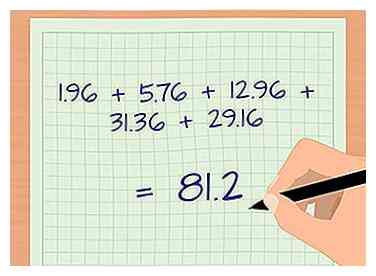 4 Cuadre cada uno de estos números y agréguelos. Cada uno de los nuevos números que acaba de calcular se cuadrará. Este paso también se ocupará de los signos negativos. Si tiene un signo negativo después de este paso o al final de su cálculo, es posible que haya olvidado este paso.
4 Cuadre cada uno de estos números y agréguelos. Cada uno de los nuevos números que acaba de calcular se cuadrará. Este paso también se ocupará de los signos negativos. Si tiene un signo negativo después de este paso o al final de su cálculo, es posible que haya olvidado este paso.  5 Divida por el número de muestra total menos 1. La fórmula se divide por N - 1 porque está corrigiendo el hecho de que no ha contado a toda una población; está tomando una muestra de la población de todos los estudiantes para hacer una estimación.[9]
5 Divida por el número de muestra total menos 1. La fórmula se divide por N - 1 porque está corrigiendo el hecho de que no ha contado a toda una población; está tomando una muestra de la población de todos los estudiantes para hacer una estimación.[9]  6 Toma la raíz cuadrada. Una vez que haya dividido por el número de muestra menos uno, tome la raíz cuadrada de este número final. Este es el último paso para calcular la desviación estándar. Hay programas estadísticos que harán este cálculo por usted después de ingresar los datos brutos.
6 Toma la raíz cuadrada. Una vez que haya dividido por el número de muestra menos uno, tome la raíz cuadrada de este número final. Este es el último paso para calcular la desviación estándar. Hay programas estadísticos que harán este cálculo por usted después de ingresar los datos brutos. 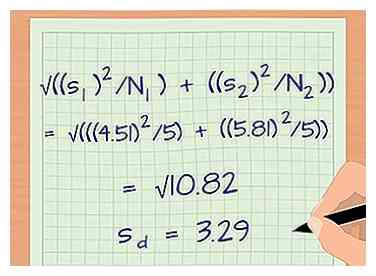 1 Calcule la varianza entre sus 2 grupos de muestra. Hasta este punto, el ejemplo solo ha tratado con 1 de los grupos de muestra. Si está intentando comparar 2 grupos, obviamente tendrá datos de ambos. Calcule la desviación estándar del segundo grupo de muestras y utilícela para calcular la varianza entre los 2 grupos experimentales. La fórmula para la varianza es sre = √ ((s1/NORTE1) + (s)2/NORTE2)).[10]
1 Calcule la varianza entre sus 2 grupos de muestra. Hasta este punto, el ejemplo solo ha tratado con 1 de los grupos de muestra. Si está intentando comparar 2 grupos, obviamente tendrá datos de ambos. Calcule la desviación estándar del segundo grupo de muestras y utilícela para calcular la varianza entre los 2 grupos experimentales. La fórmula para la varianza es sre = √ ((s1/NORTE1) + (s)2/NORTE2)).[10] 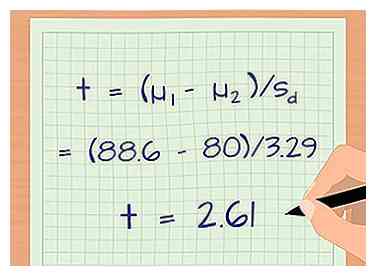 2 Calcule el puntaje t de sus datos. Un puntaje t le permite convertir sus datos en una forma que le permite compararlos con otros datos. Los puntajes T le permiten realizar una prueba t que le permite calcular la probabilidad de que dos grupos sean significativamente diferentes entre sí. La fórmula para un puntaje t es: t = (μ1 - µ2) / sre.[11]
2 Calcule el puntaje t de sus datos. Un puntaje t le permite convertir sus datos en una forma que le permite compararlos con otros datos. Los puntajes T le permiten realizar una prueba t que le permite calcular la probabilidad de que dos grupos sean significativamente diferentes entre sí. La fórmula para un puntaje t es: t = (μ1 - µ2) / sre.[11] 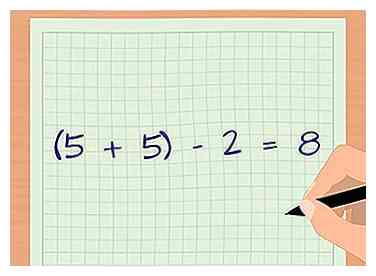 3 Determine los grados de libertad de su muestra. Al usar el puntaje t, el número de grados de libertad se determina usando el tamaño de muestra. Sume la cantidad de muestras de cada grupo y luego reste dos. Para nuestro ejemplo, los grados de libertad (d.f.) son 8 porque hay cinco muestras en el primer grupo y cinco muestras en el segundo grupo ((5 + 5) - 2 = 8).[12]
3 Determine los grados de libertad de su muestra. Al usar el puntaje t, el número de grados de libertad se determina usando el tamaño de muestra. Sume la cantidad de muestras de cada grupo y luego reste dos. Para nuestro ejemplo, los grados de libertad (d.f.) son 8 porque hay cinco muestras en el primer grupo y cinco muestras en el segundo grupo ((5 + 5) - 2 = 8).[12]  4 Use una tabla t para evaluar la significancia. Una tabla de puntajes t[13] y los grados de libertad se pueden encontrar en un libro de estadísticas estándar o en línea. Mire la fila que contiene los grados de libertad para sus datos y encuentre el valor p que corresponde a su puntaje t.
4 Use una tabla t para evaluar la significancia. Una tabla de puntajes t[13] y los grados de libertad se pueden encontrar en un libro de estadísticas estándar o en línea. Mire la fila que contiene los grados de libertad para sus datos y encuentre el valor p que corresponde a su puntaje t.  5 Considera un estudio de seguimiento. Muchos investigadores hacen un pequeño estudio piloto con algunas medidas para ayudarlos a entender cómo diseñar un estudio más amplio. Hacer otro estudio, con más mediciones, ayudará a aumentar su confianza sobre su conclusión.
5 Considera un estudio de seguimiento. Muchos investigadores hacen un pequeño estudio piloto con algunas medidas para ayudarlos a entender cómo diseñar un estudio más amplio. Hacer otro estudio, con más mediciones, ayudará a aumentar su confianza sobre su conclusión.