Los gráficos de control son una forma eficiente de analizar los datos de rendimiento para evaluar un proceso. Los cuadros de control tienen muchos usos; se pueden usar en la fabricación para probar si la maquinaria está produciendo productos dentro de las especificaciones. Además, tienen muchas aplicaciones simples, como profesores que los utilizan para evaluar los puntajes de las pruebas. Para crear un gráfico de control, es útil tener Excel; simplificará tu vida.

Pasos

  1. 1 Verifique que sus datos cumplan con los siguientes criterios:
    • Los datos generalmente deben distribuirse normalmente en torno a una media (promedio).
      • En el siguiente ejemplo, una compañía de botellas llena sus botellas a 16 oz. (media); están evaluando si su proceso está "bajo control". La cantidad en onzas de más de 16 oz normalmente se distribuye alrededor de la media.
    • Las mediciones deben ser independientes entre sí.
      • En el ejemplo, las medidas están en subgrupos. Los datos en los subgrupos deberían ser independientes del número de medición; cada punto de datos tendrá un subgrupo y un número de medición.
  2. 2 Encuentra la media de cada subgrupo.
    • Para encontrar la media, agregue todas las medidas en el subgrupo y divida por el número de mediciones en el subgrupo.
      • En el ejemplo, hay 20 subgrupos y en cada subgrupo hay 4 medidas.
  3. 3 Encuentra la media de todos los medios del paso anterior (X).
    • Esto le dará la media general de todos los puntos de datos.
    • La media global será la línea central en el gráfico (CL), que es 13.75 para nuestro ejemplo.
  4. 4 Calcule la desviación estándar (S) de los puntos de datos (ver consejos).
  5. 5 Calcule los límites de control superior e inferior (UCL, LCL) usando la siguiente fórmula:
    • UCL = CL + 3 * S
    • LCL = CL - 3 * S
    • La fórmula representa 3 desviaciones estándar por encima y 3 desviaciones estándar por debajo de la media, respectivamente.
  6. 6 Consulte la tabla a continuación con los pasos 7 a 10.
  7. 7 Dibuja una línea en cada desviación.
    • En el ejemplo anterior, hay una línea dibujada en una, dos y tres desviaciones estándar (sigma) lejos de la media.
      • La zona C está a 1 sigma de distancia de la media (verde).
      • La zona B está a 2 sigma de distancia de la media (amarilla).
      • La zona A está a 3 sigma de la media (roja).
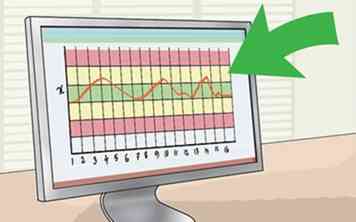  8. 8 Graficar el gráfico de control de barras X, graficando el subgrupo significa (eje x) versos de mediciones (eje y). Tu gráfica debería verse más o menos así:
  9. 9 Evalúe el gráfico para ver si el proceso está fuera de control. El gráfico está fuera de control si cualquiera de los siguientes es verdadero:
    • Cualquier punto cae más allá de la zona roja (arriba o debajo de la línea 3-sigma).
    • 8 puntos consecutivos caen en un lado de la línea central.
    • 2 de 3 puntos consecutivos caen dentro de la zona A.
    • 4 de 5 puntos consecutivos caen dentro de la zona A y / o zona B.
    • 15 puntos consecutivos están dentro de la Zona C.
    • 8 puntos consecutivos no en la zona C.
  10. 10 Indique si el sistema está bajo control o fuera de control.

Gráficos de control de muestra

Tabla de control de muestra Gráfico de control de muestra para subgrupos Gráfico de control de muestra para grupos múltiples