Por diversos motivos, es posible que necesite definir el valor máximo o mínimo de una función cuadrática seleccionada. Puede encontrar el máximo o mínimo si su función original está escrita en forma general, , o en forma estándar, . Finalmente, también puede usar algunos cálculos básicos para definir el máximo o mínimo de cualquier función cuadrática.
Método uno de tres:
A partir de la forma general de la función
-
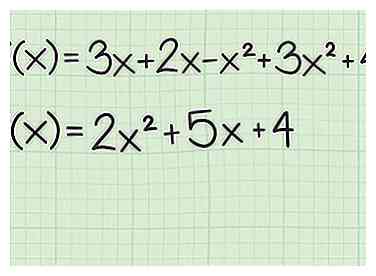 1 Configure la función en forma general. Una función cuadrática es aquella que tiene un término. Puede o no contener un término sin un exponente No habrá exponentes más grandes que 2. La forma general es . Si es necesario, combine términos similares y reorganice para establecer la función en esta forma general.[1]
1 Configure la función en forma general. Una función cuadrática es aquella que tiene un término. Puede o no contener un término sin un exponente No habrá exponentes más grandes que 2. La forma general es . Si es necesario, combine términos similares y reorganice para establecer la función en esta forma general.[1] - Por ejemplo, supongamos que comienzas con . Combina el términos y el términos para obtener lo siguiente en forma general:
- Por ejemplo, supongamos que comienzas con . Combina el términos y el términos para obtener lo siguiente en forma general:
-
 2 Determine la dirección del gráfico. Una función cuadrática da como resultado el gráfico de una parábola. La parábola se abre hacia arriba o hacia abajo. Si , el coeficiente de término, es positivo, entonces la parábola se abre hacia arriba. Si es negativo, entonces la parábola se abre hacia abajo. Mira los siguientes ejemplos:[2]
2 Determine la dirección del gráfico. Una función cuadrática da como resultado el gráfico de una parábola. La parábola se abre hacia arriba o hacia abajo. Si , el coeficiente de término, es positivo, entonces la parábola se abre hacia arriba. Si es negativo, entonces la parábola se abre hacia abajo. Mira los siguientes ejemplos:[2] - por , entonces la parábola se abre hacia arriba.
- por , entonces la parábola se abre hacia abajo.
- por , entonces la parábola se abre hacia arriba.
- Si la parábola se abre hacia arriba, encontrará su valor mínimo. Si la parábola se abre hacia abajo, encontrará su valor máximo.
-
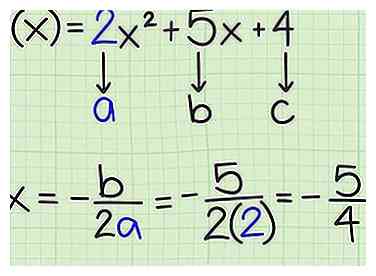 3 Calcula -b / 2a. El valor de te dice el valor del vértice de la parábola. Cuando la función cuadrática está escrita en su forma general de , usa los coeficientes de y términos de la siguiente manera:
3 Calcula -b / 2a. El valor de te dice el valor del vértice de la parábola. Cuando la función cuadrática está escrita en su forma general de , usa los coeficientes de y términos de la siguiente manera: - Para una función , y . Por lo tanto, encuentre el valor x del vértice como:
- Como segundo ejemplo, considere la función . En este ejemplo, y . Por lo tanto, encuentre el valor x del vértice como:
- Para una función , y . Por lo tanto, encuentre el valor x del vértice como:
-
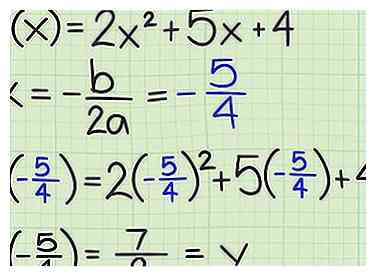 4 Encuentra el valor f (x) correspondiente. Inserte el valor de x que acaba de calcular en la función para encontrar el valor correspondiente de f (x). Este será el mínimo o el máximo de la función.
4 Encuentra el valor f (x) correspondiente. Inserte el valor de x que acaba de calcular en la función para encontrar el valor correspondiente de f (x). Este será el mínimo o el máximo de la función. - Para el primer ejemplo anterior, , calculó el valor de x para que el vértice sea . Entrar en lugar de en la función para encontrar el valor máximo:
- Para el segundo ejemplo anterior, , encontraste que el vértice estaba en . Insertar en lugar de en la función para encontrar el valor máximo:
- Para el primer ejemplo anterior, , calculó el valor de x para que el vértice sea . Entrar en lugar de en la función para encontrar el valor máximo:
-
 5 Informe sus resultados. Revisa la pregunta que te hicieron. Si se le piden las coordenadas del vértice, debe informar el y (o ) valores. Si solo se le solicita el máximo o mínimo, solo necesita informar el (o valor) Consulte de nuevo el valor de coeficiente para asegurarse de tener un máximo o un mínimo.
5 Informe sus resultados. Revisa la pregunta que te hicieron. Si se le piden las coordenadas del vértice, debe informar el y (o ) valores. Si solo se le solicita el máximo o mínimo, solo necesita informar el (o valor) Consulte de nuevo el valor de coeficiente para asegurarse de tener un máximo o un mínimo. - Para el primer ejemplo, , El valor de es positivo, por lo que informará el valor mínimo. El vértice está en y el valor mínimo es .
- Para el segundo ejemplo, , El valor de es negativo, por lo que informará el valor máximo. El vértice está en y el valor máximo es .
Método dos de tres:
Usando el formulario estándar o vértice
-
 1 Escribe tu función cuadrática en forma estándar o vértice. La forma estándar de una función cuadrática general, que también se puede llamar forma de vértice, se ve así:[3]
1 Escribe tu función cuadrática en forma estándar o vértice. La forma estándar de una función cuadrática general, que también se puede llamar forma de vértice, se ve así:[3] - Si su función ya se le ha asignado de esta forma, solo necesita reconocer las variables , y . Si su función comienza en la forma general , deberás completar el cuadrado para volver a escribirlo en forma de vértice.
- Para revisar cómo completar el cuadrado, vea Completar el cuadrado.
-
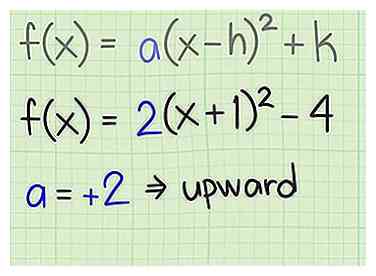 2 Determine la dirección del gráfico. Al igual que con una función cuadrática escrita en su forma general, puede indicar la dirección de la parábola observando el coeficiente . Si en esta forma estándar es positiva, entonces la parábola se abre hacia arriba. Si es negativo, entonces la parábola se abre hacia abajo. Mira los siguientes ejemplos:[4]
2 Determine la dirección del gráfico. Al igual que con una función cuadrática escrita en su forma general, puede indicar la dirección de la parábola observando el coeficiente . Si en esta forma estándar es positiva, entonces la parábola se abre hacia arriba. Si es negativo, entonces la parábola se abre hacia abajo. Mira los siguientes ejemplos:[4] - por , , que es positivo, entonces la parábola se abre hacia arriba.
- por , , que es negativo, entonces la parábola se abre hacia abajo.
- Si la parábola se abre hacia arriba, encontrará su valor mínimo. Si la parábola se abre hacia abajo, encontrará su valor máximo.
-
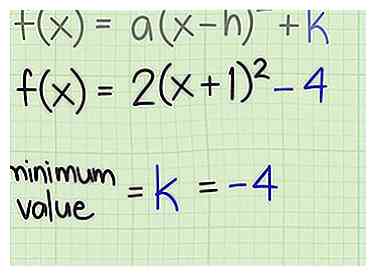 3 Identifica el valor mínimo o máximo. Cuando la función se escribe en forma estándar, encontrar el valor mínimo o máximo es tan simple como establecer el valor de la variable . Para las dos funciones de ejemplo dadas anteriormente, estos valores son:
3 Identifica el valor mínimo o máximo. Cuando la función se escribe en forma estándar, encontrar el valor mínimo o máximo es tan simple como establecer el valor de la variable . Para las dos funciones de ejemplo dadas anteriormente, estos valores son: - por , . Este es el valor mínimo de la función porque esta parábola se abre hacia arriba.
- por , . Este es el valor máximo de la función, porque esta parábola se abre hacia abajo.
-
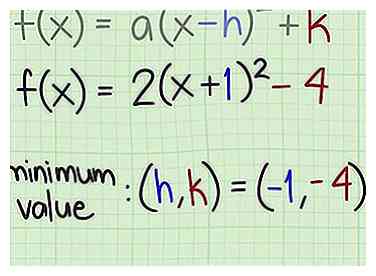 4 Encuentra el vértice. Si se le piden las coordenadas del valor mínimo o máximo, el punto será . Tenga en cuenta, sin embargo, que en la forma estándar de la ecuación, el término entre paréntesis es , entonces necesitas el signo opuesto al número que sigue al .
4 Encuentra el vértice. Si se le piden las coordenadas del valor mínimo o máximo, el punto será . Tenga en cuenta, sin embargo, que en la forma estándar de la ecuación, el término entre paréntesis es , entonces necesitas el signo opuesto al número que sigue al . - por , el término entre paréntesis es (x + 1), que se puede reescribir como (x - (- 1)). Así, . Por lo tanto, las coordenadas del vértice para esta función son .
- por , el término dentro del paréntesis es (x-2). Por lo tanto, . Las coordenadas del vértice son (2, 2).
Método tres de tres:
Usar el cálculo para derivar el mínimo o el máximo
-
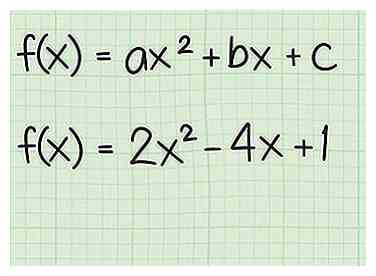 1 Comience con la forma general. Escribe tu función cuadrática en forma general, . Si es necesario, puede necesitar combinar términos similares y reorganizar para obtener la forma correcta.[5]
1 Comience con la forma general. Escribe tu función cuadrática en forma general, . Si es necesario, puede necesitar combinar términos similares y reorganizar para obtener la forma correcta.[5] - Comience con la función de muestra .
-
 2 Usa la regla de poder para encontrar la primera derivada. Usando el cálculo básico de primer año, puede encontrar la primera derivada de la función cuadrática general que se debe .[6]
2 Usa la regla de poder para encontrar la primera derivada. Usando el cálculo básico de primer año, puede encontrar la primera derivada de la función cuadrática general que se debe .[6] - Para la función de muestra , encuentra la derivada como:
- Para la función de muestra , encuentra la derivada como:
-
 3 Establezca la derivada igual a cero. Recuerde que la derivada de una función le dice la pendiente de la función en ese punto seleccionado. El mínimo o máximo de una función ocurre cuando la pendiente es cero. Por lo tanto, para encontrar dónde ocurre el mínimo o el máximo, establezca la derivada igual a cero. Continúe con el problema de muestra de arriba:[7]
3 Establezca la derivada igual a cero. Recuerde que la derivada de una función le dice la pendiente de la función en ese punto seleccionado. El mínimo o máximo de una función ocurre cuando la pendiente es cero. Por lo tanto, para encontrar dónde ocurre el mínimo o el máximo, establezca la derivada igual a cero. Continúe con el problema de muestra de arriba:[7] -
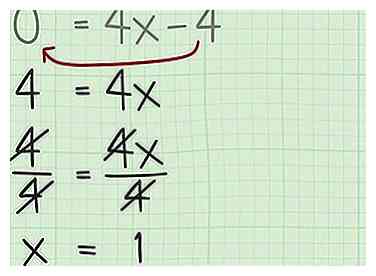 4 Solución para x. Usa las reglas básicas del álgebra para reordenar la función y resolver el valor de x, cuando la derivada es igual a cero. Esta solución le dirá la coordenada x del vértice de la función, que es donde ocurrirá el máximo o el mínimo.[8]
4 Solución para x. Usa las reglas básicas del álgebra para reordenar la función y resolver el valor de x, cuando la derivada es igual a cero. Esta solución le dirá la coordenada x del vértice de la función, que es donde ocurrirá el máximo o el mínimo.[8] -
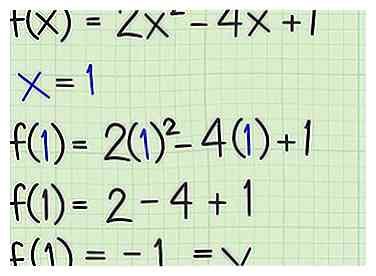 5 Inserta el valor resuelto de x en la función original. El valor mínimo o máximo de la función será el valor de en el seleccionado posición. Inserta tu valor de en la función original y resuelve para encontrar el mínimo o el máximo.[9]
5 Inserta el valor resuelto de x en la función original. El valor mínimo o máximo de la función será el valor de en el seleccionado posición. Inserta tu valor de en la función original y resuelve para encontrar el mínimo o el máximo.[9] - Para la función a ,
- Para la función a ,
-
 6 Informe su solución. La solución te da el vértice del punto máximo o mínimo. Para esta función de muestra, , el vértice ocurre en . El coeficiente es positivo, por lo que la función se abre hacia arriba. Por lo tanto, el valor mínimo de la función es la coordenada y del vértice, que es .[10]
6 Informe su solución. La solución te da el vértice del punto máximo o mínimo. Para esta función de muestra, , el vértice ocurre en . El coeficiente es positivo, por lo que la función se abre hacia arriba. Por lo tanto, el valor mínimo de la función es la coordenada y del vértice, que es .[10]
 Minotauromaquia
Minotauromaquia
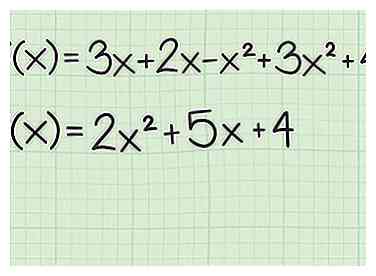 1 Configure la función en forma general. Una función cuadrática es aquella que tiene un
1 Configure la función en forma general. Una función cuadrática es aquella que tiene un  2 Determine la dirección del gráfico. Una función cuadrática da como resultado el gráfico de una parábola. La parábola se abre hacia arriba o hacia abajo. Si
2 Determine la dirección del gráfico. Una función cuadrática da como resultado el gráfico de una parábola. La parábola se abre hacia arriba o hacia abajo. Si 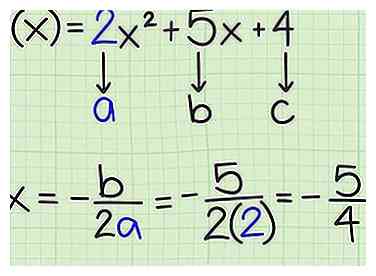 3 Calcula -b / 2a. El valor de
3 Calcula -b / 2a. El valor de 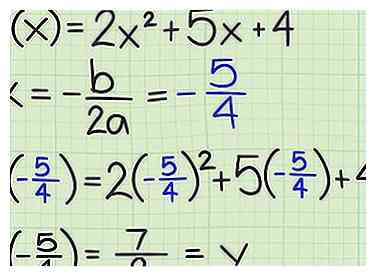 4 Encuentra el valor f (x) correspondiente. Inserte el valor de x que acaba de calcular en la función para encontrar el valor correspondiente de f (x). Este será el mínimo o el máximo de la función.
4 Encuentra el valor f (x) correspondiente. Inserte el valor de x que acaba de calcular en la función para encontrar el valor correspondiente de f (x). Este será el mínimo o el máximo de la función.  5 Informe sus resultados. Revisa la pregunta que te hicieron. Si se le piden las coordenadas del vértice, debe informar el
5 Informe sus resultados. Revisa la pregunta que te hicieron. Si se le piden las coordenadas del vértice, debe informar el  1 Escribe tu función cuadrática en forma estándar o vértice. La forma estándar de una función cuadrática general, que también se puede llamar forma de vértice, se ve así:[3]
1 Escribe tu función cuadrática en forma estándar o vértice. La forma estándar de una función cuadrática general, que también se puede llamar forma de vértice, se ve así:[3] 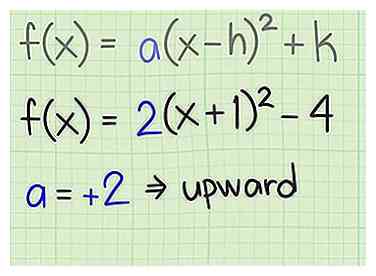 2 Determine la dirección del gráfico. Al igual que con una función cuadrática escrita en su forma general, puede indicar la dirección de la parábola observando el coeficiente
2 Determine la dirección del gráfico. Al igual que con una función cuadrática escrita en su forma general, puede indicar la dirección de la parábola observando el coeficiente 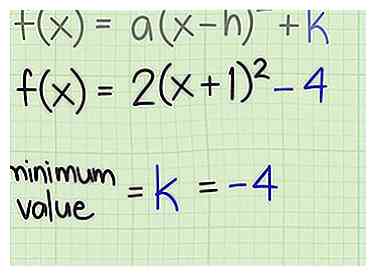 3 Identifica el valor mínimo o máximo. Cuando la función se escribe en forma estándar, encontrar el valor mínimo o máximo es tan simple como establecer el valor de la variable
3 Identifica el valor mínimo o máximo. Cuando la función se escribe en forma estándar, encontrar el valor mínimo o máximo es tan simple como establecer el valor de la variable 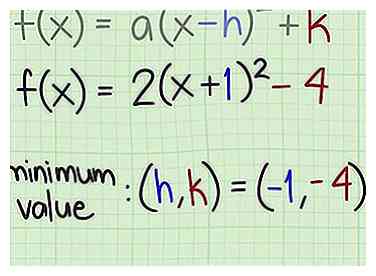 4 Encuentra el vértice. Si se le piden las coordenadas del valor mínimo o máximo, el punto será
4 Encuentra el vértice. Si se le piden las coordenadas del valor mínimo o máximo, el punto será 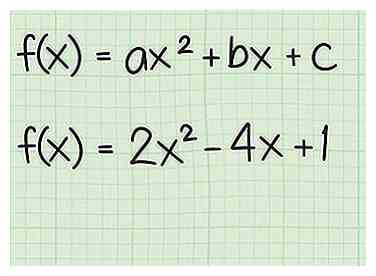 1 Comience con la forma general. Escribe tu función cuadrática en forma general,
1 Comience con la forma general. Escribe tu función cuadrática en forma general,  2 Usa la regla de poder para encontrar la primera derivada. Usando el cálculo básico de primer año, puede encontrar la primera derivada de la función cuadrática general que se debe
2 Usa la regla de poder para encontrar la primera derivada. Usando el cálculo básico de primer año, puede encontrar la primera derivada de la función cuadrática general que se debe  3 Establezca la derivada igual a cero. Recuerde que la derivada de una función le dice la pendiente de la función en ese punto seleccionado. El mínimo o máximo de una función ocurre cuando la pendiente es cero. Por lo tanto, para encontrar dónde ocurre el mínimo o el máximo, establezca la derivada igual a cero. Continúe con el problema de muestra de arriba:[7]
3 Establezca la derivada igual a cero. Recuerde que la derivada de una función le dice la pendiente de la función en ese punto seleccionado. El mínimo o máximo de una función ocurre cuando la pendiente es cero. Por lo tanto, para encontrar dónde ocurre el mínimo o el máximo, establezca la derivada igual a cero. Continúe con el problema de muestra de arriba:[7] 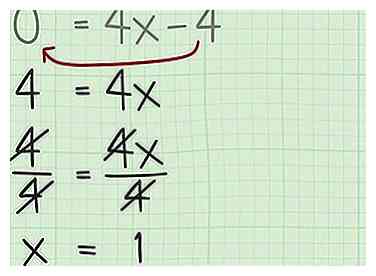 4 Solución para x. Usa las reglas básicas del álgebra para reordenar la función y resolver el valor de x, cuando la derivada es igual a cero. Esta solución le dirá la coordenada x del vértice de la función, que es donde ocurrirá el máximo o el mínimo.[8]
4 Solución para x. Usa las reglas básicas del álgebra para reordenar la función y resolver el valor de x, cuando la derivada es igual a cero. Esta solución le dirá la coordenada x del vértice de la función, que es donde ocurrirá el máximo o el mínimo.[8] 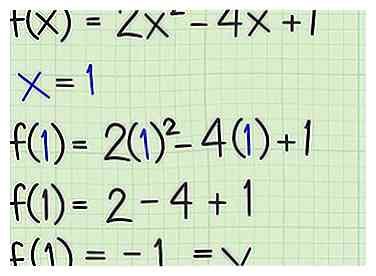 5 Inserta el valor resuelto de x en la función original. El valor mínimo o máximo de la función será el valor de
5 Inserta el valor resuelto de x en la función original. El valor mínimo o máximo de la función será el valor de  6 Informe su solución. La solución te da el vértice del punto máximo o mínimo. Para esta función de muestra,
6 Informe su solución. La solución te da el vértice del punto máximo o mínimo. Para esta función de muestra,