Si sabes cómo multiplicar dos matrices juntas, estás en camino de "dividir" una matriz por otra. Esa palabra está entre comillas porque las matrices técnicamente no se pueden dividir. En cambio, multiplicamos una matriz por la inverso de otra matriz. Estos cálculos se usan comúnmente para resolver sistemas de ecuaciones lineales.[1]
Parte uno de tres:
Confirmando que la "división" es posible
-
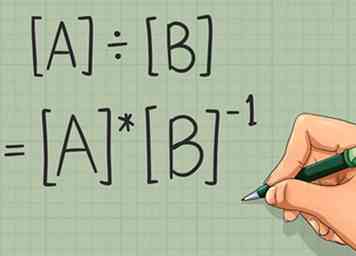 1 Comprender la división de la matriz" Técnicamente, no existe la división de matriz. Dividir una matriz por otra matriz es una función indefinida.[2] El equivalente más cercano se multiplica por el inverso de otra matriz. En otras palabras, mientras [A] ÷ [B] no está definido, puede resolver el problema [A] * [B]-1. Dado que estas dos ecuaciones serían equivalentes para cantidades escalares, esto "se siente" como una división de matriz, pero es importante usar la terminología correcta.
1 Comprender la división de la matriz" Técnicamente, no existe la división de matriz. Dividir una matriz por otra matriz es una función indefinida.[2] El equivalente más cercano se multiplica por el inverso de otra matriz. En otras palabras, mientras [A] ÷ [B] no está definido, puede resolver el problema [A] * [B]-1. Dado que estas dos ecuaciones serían equivalentes para cantidades escalares, esto "se siente" como una división de matriz, pero es importante usar la terminología correcta. - Tenga en cuenta que [A] * [B]-1 y B]-1 * [A] no son el mismo problema. Es posible que deba resolver ambos para encontrar todas las soluciones posibles.
- Por ejemplo, en lugar de , escribir .
Es posible que también necesite calcular , que puede tener una respuesta diferente.
-
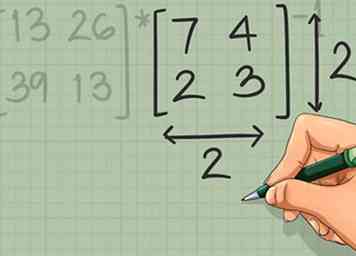 2 Confirme que la "matriz del divisor" es cuadrada. Para tomar el inverso de una matriz, debe ser una matriz cuadrada, con el mismo número de filas y columnas. Si la matriz que planea invertir no es cuadrada, no existe una solución única para el problema.[3]
2 Confirme que la "matriz del divisor" es cuadrada. Para tomar el inverso de una matriz, debe ser una matriz cuadrada, con el mismo número de filas y columnas. Si la matriz que planea invertir no es cuadrada, no existe una solución única para el problema.[3] - El término "matriz divisoria" es un poco flojo, ya que técnicamente no es un problema de división. Para [A] * [B]-1, esto se refiere a la matriz [B]. En nuestro problema de ejemplo, esto es .
- Una matriz que tiene una inversa se llama "invertible" o "no singular". Las matrices sin inversa son "singulares".
-
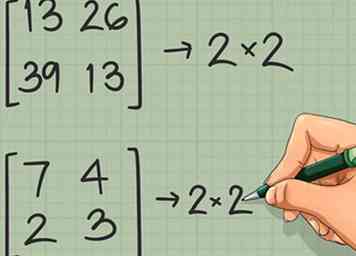 3 Verifique que las dos matrices se puedan multiplicar juntas. Para multiplicar dos matrices juntas, el número de columnas en la primera matriz debe ser igual al número de filas en la segunda matriz.[4] Si esto no funciona en ninguno de los arreglos ([A] * [B]-1 o [B]-1 * [A]), no hay solución al problema.
3 Verifique que las dos matrices se puedan multiplicar juntas. Para multiplicar dos matrices juntas, el número de columnas en la primera matriz debe ser igual al número de filas en la segunda matriz.[4] Si esto no funciona en ninguno de los arreglos ([A] * [B]-1 o [B]-1 * [A]), no hay solución al problema. - Por ejemplo, si [A] es una matriz de 4 x 3 (4 filas, 3 columnas) y [B] es una matriz de 2 x 2 (2 filas, 2 columnas), no hay solución. [A] * [B]-1 no funciona desde 3 ≠ 2, y [B]-1 * [A] no funciona desde 2 ≠ 4.
- Tenga en cuenta que el inverso [B]-1 siempre tiene el mismo número de filas y columnas que la matriz original [B]. No es necesario calcular el inverso para completar este paso.
- En nuestro problema de ejemplo, ambas matrices son 2 x 2, por lo que se pueden multiplicar en cualquier orden.
-
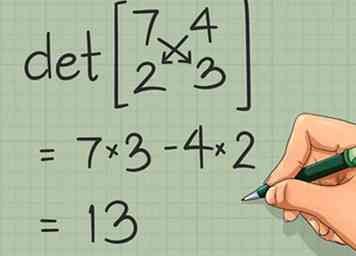 4 Encuentra el determinante de una matriz de 2 x 2. Hay un requisito más que verificar antes de poder tomar el inverso de una matriz. El determinante de la matriz debe ser distinto de cero. Si el determinante es cero, la matriz no tiene un inverso. Aquí se explica cómo encontrar el determinante en el caso más simple, la matriz 2 x 2:
4 Encuentra el determinante de una matriz de 2 x 2. Hay un requisito más que verificar antes de poder tomar el inverso de una matriz. El determinante de la matriz debe ser distinto de cero. Si el determinante es cero, la matriz no tiene un inverso. Aquí se explica cómo encontrar el determinante en el caso más simple, la matriz 2 x 2: - Matriz 2 x 2: El determinante de la matriz es ad - bc.[5] En otras palabras, tome el producto de la diagonal principal (arriba a la izquierda a la parte inferior derecha), luego restar el producto de la antidiagonal (arriba a la derecha a abajo a la izquierda).
- Por ejemplo, la matriz tiene el determinante (7) (3) - (4) (2) = 21 - 8 = 13. Esto es distinto de cero, por lo que es posible encontrar el inverso.
-
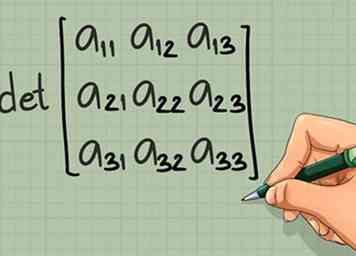 5 Encuentra el determinante de una matriz más grande. Si su matriz es 3 x 3 o superior, encontrar el determinante requiere un poco más de trabajo:
5 Encuentra el determinante de una matriz más grande. Si su matriz es 3 x 3 o superior, encontrar el determinante requiere un poco más de trabajo: - Matriz 3 x 3: Elija cualquier elemento y tache la fila y columna a la que pertenece. Encuentre el determinante de la matriz 2 x 2 restante, multiplique por el elemento elegido y haga referencia a una tabla de signos de matriz para determinar el signo. Repita esto para los otros dos elementos en la misma fila o columna que el primero que eligió, luego sume los tres factores determinantes. Lea este artículo para obtener instrucciones paso a paso y consejos para acelerar esto.
- Matrices más grandes: Se recomienda el uso de una calculadora gráfica o software. El método es similar al método de matriz de 3 x 3, pero es tedioso a mano.[6] Por ejemplo, para encontrar el determinante de una matriz de 4 x 4, debe encontrar los determinantes de cuatro matrices de 3 x 3.
-
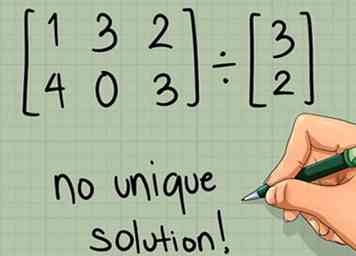 6 Continúa en. Si su matriz no es cuadrada, o si su determinante es cero, escriba "ninguna solución única". El problema esta completo Si la matriz es cuadrada y su determinante es distinto de cero, continúe con la siguiente sección para el próximo paso: encontrar el inverso.
6 Continúa en. Si su matriz no es cuadrada, o si su determinante es cero, escriba "ninguna solución única". El problema esta completo Si la matriz es cuadrada y su determinante es distinto de cero, continúe con la siguiente sección para el próximo paso: encontrar el inverso.
Parte dos de tres:
Invertir la matriz
-
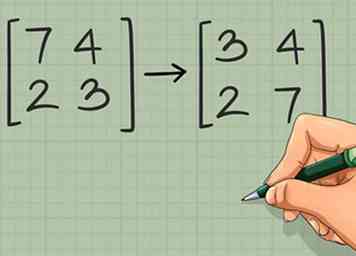 1 Cambie las posiciones de los elementos en la diagonal principal de 2 x 2. Si su matriz es 2 x 2, puede usar un atajo para hacer este cálculo mucho más fácil.[7] El primer paso en este acceso directo implica cambiar el elemento superior izquierdo con el elemento inferior derecho. Por ejemplo:
1 Cambie las posiciones de los elementos en la diagonal principal de 2 x 2. Si su matriz es 2 x 2, puede usar un atajo para hacer este cálculo mucho más fácil.[7] El primer paso en este acceso directo implica cambiar el elemento superior izquierdo con el elemento inferior derecho. Por ejemplo: - →
- Nota: La mayoría de las personas usa calculadoras para encontrar el inverso de una matriz de 3 x 3 o superior. Si desea calcularlo a mano, consulte el final de esta sección.
-
 2 Tome el opuesto de los otros dos elementos, pero déjelos en posición. En otras palabras, multiplicar la parte superior derecho y abajo izquierda elementos por -1:
2 Tome el opuesto de los otros dos elementos, pero déjelos en posición. En otras palabras, multiplicar la parte superior derecho y abajo izquierda elementos por -1: - →
-
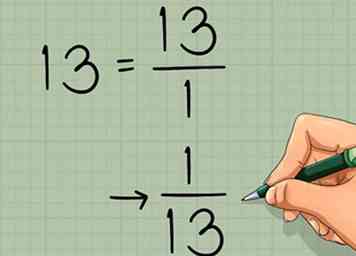 3 Toma el recíproco del determinante. Encontró el determinante de esta matriz en la sección anterior, por lo que no es necesario calcularla por segunda vez. Simplemente escriba el 1 / (determinante) recíproco:
3 Toma el recíproco del determinante. Encontró el determinante de esta matriz en la sección anterior, por lo que no es necesario calcularla por segunda vez. Simplemente escriba el 1 / (determinante) recíproco: - En nuestro ejemplo, el determinante es 13. El recíproco de esto es .
-
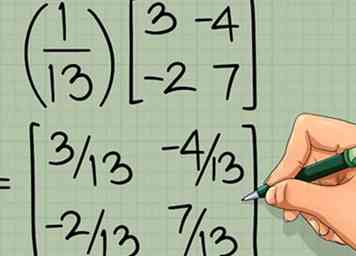 4 Multiplica la nueva matriz por el recíproco del determinante. Multiplica cada elemento de la nueva matriz por el recíproco que acabas de encontrar. La matriz resultante es la inversa de la matriz 2 x 2:
4 Multiplica la nueva matriz por el recíproco del determinante. Multiplica cada elemento de la nueva matriz por el recíproco que acabas de encontrar. La matriz resultante es la inversa de la matriz 2 x 2: -
=
-
-
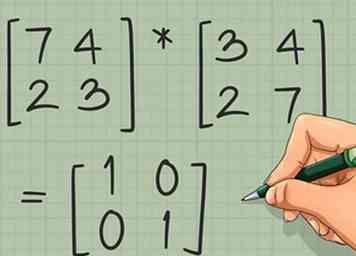 5 Confirma que el inverso es correcto. Para verificar tu trabajo, multiplica el inverso por la matriz original. Si el inverso es correcto, su producto siempre será la matriz de identidad, Si la matemática se retira, continúe con la siguiente sección para completar su problema.
5 Confirma que el inverso es correcto. Para verificar tu trabajo, multiplica el inverso por la matriz original. Si el inverso es correcto, su producto siempre será la matriz de identidad, Si la matemática se retira, continúe con la siguiente sección para completar su problema. - Para el problema de ejemplo, multiplique .
- Aquí hay un repaso sobre cómo multiplicar matrices.
- Nota: la multiplicación de la matriz no es conmutativa: el orden de los factores es importante. Sin embargo, al multiplicar una matriz por su inversa, ambas opciones darán como resultado la matriz de identidad.[8]
-
 6 Revise la inversión de la matriz para matrices de 3 x 3 o más. A menos que esté aprendiendo este proceso por primera vez, ahorre tiempo usando una calculadora gráfica o software matemático para matrices más grandes. Si necesita calcularlo a mano, aquí hay un resumen rápido de un método:[9][10]
6 Revise la inversión de la matriz para matrices de 3 x 3 o más. A menos que esté aprendiendo este proceso por primera vez, ahorre tiempo usando una calculadora gráfica o software matemático para matrices más grandes. Si necesita calcularlo a mano, aquí hay un resumen rápido de un método:[9][10] - Adhiera la matriz de identidad I al lado derecho de su matriz. Por ejemplo, [B] → [B | YO ]. La matriz de identidad tiene elementos "1" a lo largo de la diagonal principal y elementos "0" en todas las otras posiciones.
- Realice operaciones de fila para reducir la matriz hasta que el lado izquierdo esté en forma escalonada, luego continúe reduciendo hasta que el lado izquierdo sea la matriz de identidad.
- Una vez que se completa la operación, su matriz estará en la forma [I | segundo-1] En otras palabras, el lado derecho será el inverso de la matriz original.
Parte tres de tres:
Multiplicar matrices para completar el problema
-
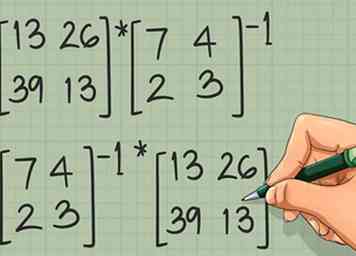 1 Escribe ambas ecuaciones posibles. En "matemáticas ordinarias" con cantidades escalares, la multiplicación es conmutativa; 2 x 6 = 6 x 2. Esto no es cierto para las matrices, por lo que puede necesitar resolver dos problemas:
1 Escribe ambas ecuaciones posibles. En "matemáticas ordinarias" con cantidades escalares, la multiplicación es conmutativa; 2 x 6 = 6 x 2. Esto no es cierto para las matrices, por lo que puede necesitar resolver dos problemas: - [A] * [B]-1 es la solución X para el problema X[B] = [A].
- [SEGUNDO]-1 * [A] es la solución X para el problema [B]X = [A].
- Si esto es parte de una ecuación, asegúrese de realizar la misma operación en ambos lados. Si [A] = [C], entonces [B]-1[A] lo hace no igual [C] [B]-1, porque el [B]-1 está en el lado izquierdo de [A] pero el lado derecho de [C].[11]
-
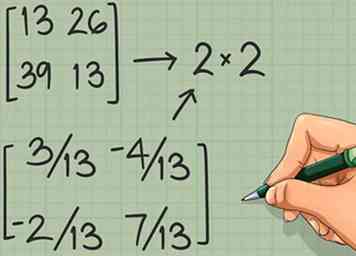 2 Encuentra las dimensiones de tu respuesta. Las dimensiones de la matriz final son las dimensiones externas de los dos factores. Tiene el mismo número de filas que la primera matriz y el mismo número de columnas que la segunda matriz.
2 Encuentra las dimensiones de tu respuesta. Las dimensiones de la matriz final son las dimensiones externas de los dos factores. Tiene el mismo número de filas que la primera matriz y el mismo número de columnas que la segunda matriz. - Volviendo a nuestro ejemplo original, ambos y son matrices de 2 x 2, por lo que las dimensiones de la respuesta son también 2 x 2.
- Para tomar un ejemplo más complicado, si [A] es un 4 x 3 matriz y [B]-1 es un 3 x 3 matriz, luego la matriz [A] * [B]-1 tiene dimensiones 4 x 3.
-
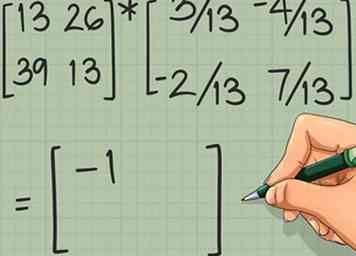 3 Encuentra el valor del primer elemento. Consulte el artículo vinculado para obtener instrucciones completas o actualice su memoria con este resumen:
3 Encuentra el valor del primer elemento. Consulte el artículo vinculado para obtener instrucciones completas o actualice su memoria con este resumen: - Para encontrar la fila 1, columna 1 de [A] [B]-1, encuentre el producto escalar de [A] fila 1 y [B]-1 columna 1. Es decir, para una matriz de 2 x 2, calcule .
- En nuestro ejemplo , la fila 1 de la columna 1 de nuestra respuesta es:
-
 4 Repita el proceso del producto escalar para cada posición en su matriz. Por ejemplo, el elemento en la posición 2,1 es el producto escalar de [A] fila 2 y [B]-1 columna 1. Trate de completar el ejemplo por su cuenta. Deberías obtener las siguientes respuestas:
4 Repita el proceso del producto escalar para cada posición en su matriz. Por ejemplo, el elemento en la posición 2,1 es el producto escalar de [A] fila 2 y [B]-1 columna 1. Trate de completar el ejemplo por su cuenta. Deberías obtener las siguientes respuestas: - Si necesita encontrar la otra solución,
 Minotauromaquia
Minotauromaquia
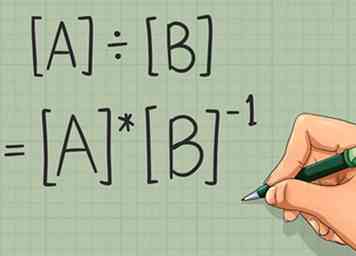 1 Comprender la división de la matriz" Técnicamente, no existe la división de matriz. Dividir una matriz por otra matriz es una función indefinida.[2] El equivalente más cercano se multiplica por el inverso de otra matriz. En otras palabras, mientras [A] ÷ [B] no está definido, puede resolver el problema [A] * [B]-1. Dado que estas dos ecuaciones serían equivalentes para cantidades escalares, esto "se siente" como una división de matriz, pero es importante usar la terminología correcta.
1 Comprender la división de la matriz" Técnicamente, no existe la división de matriz. Dividir una matriz por otra matriz es una función indefinida.[2] El equivalente más cercano se multiplica por el inverso de otra matriz. En otras palabras, mientras [A] ÷ [B] no está definido, puede resolver el problema [A] * [B]-1. Dado que estas dos ecuaciones serían equivalentes para cantidades escalares, esto "se siente" como una división de matriz, pero es importante usar la terminología correcta. 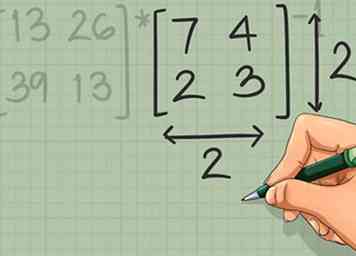 2 Confirme que la "matriz del divisor" es cuadrada. Para tomar el inverso de una matriz, debe ser una matriz cuadrada, con el mismo número de filas y columnas. Si la matriz que planea invertir no es cuadrada, no existe una solución única para el problema.[3]
2 Confirme que la "matriz del divisor" es cuadrada. Para tomar el inverso de una matriz, debe ser una matriz cuadrada, con el mismo número de filas y columnas. Si la matriz que planea invertir no es cuadrada, no existe una solución única para el problema.[3] 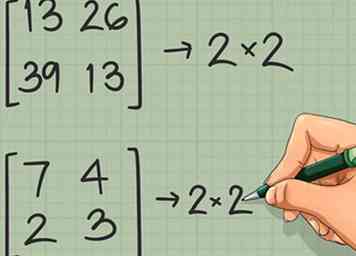 3 Verifique que las dos matrices se puedan multiplicar juntas. Para multiplicar dos matrices juntas, el número de columnas en la primera matriz debe ser igual al número de filas en la segunda matriz.[4] Si esto no funciona en ninguno de los arreglos ([A] * [B]-1 o [B]-1 * [A]), no hay solución al problema.
3 Verifique que las dos matrices se puedan multiplicar juntas. Para multiplicar dos matrices juntas, el número de columnas en la primera matriz debe ser igual al número de filas en la segunda matriz.[4] Si esto no funciona en ninguno de los arreglos ([A] * [B]-1 o [B]-1 * [A]), no hay solución al problema. 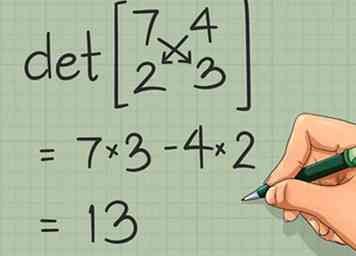 4 Encuentra el determinante de una matriz de 2 x 2. Hay un requisito más que verificar antes de poder tomar el inverso de una matriz. El determinante de la matriz debe ser distinto de cero. Si el determinante es cero, la matriz no tiene un inverso. Aquí se explica cómo encontrar el determinante en el caso más simple, la matriz 2 x 2:
4 Encuentra el determinante de una matriz de 2 x 2. Hay un requisito más que verificar antes de poder tomar el inverso de una matriz. El determinante de la matriz debe ser distinto de cero. Si el determinante es cero, la matriz no tiene un inverso. Aquí se explica cómo encontrar el determinante en el caso más simple, la matriz 2 x 2: 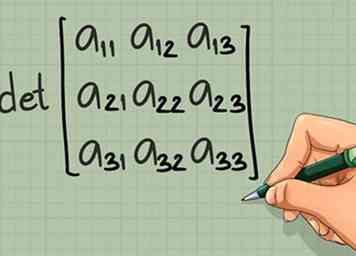 5 Encuentra el determinante de una matriz más grande. Si su matriz es 3 x 3 o superior, encontrar el determinante requiere un poco más de trabajo:
5 Encuentra el determinante de una matriz más grande. Si su matriz es 3 x 3 o superior, encontrar el determinante requiere un poco más de trabajo: 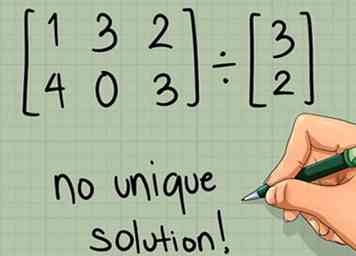 6 Continúa en. Si su matriz no es cuadrada, o si su determinante es cero, escriba "ninguna solución única". El problema esta completo Si la matriz es cuadrada y su determinante es distinto de cero, continúe con la siguiente sección para el próximo paso: encontrar el inverso.
6 Continúa en. Si su matriz no es cuadrada, o si su determinante es cero, escriba "ninguna solución única". El problema esta completo Si la matriz es cuadrada y su determinante es distinto de cero, continúe con la siguiente sección para el próximo paso: encontrar el inverso. 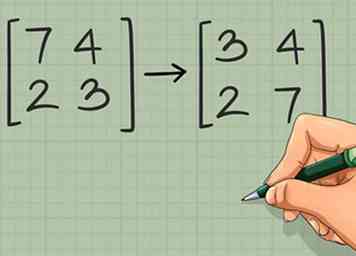 1 Cambie las posiciones de los elementos en la diagonal principal de 2 x 2. Si su matriz es 2 x 2, puede usar un atajo para hacer este cálculo mucho más fácil.[7] El primer paso en este acceso directo implica cambiar el elemento superior izquierdo con el elemento inferior derecho. Por ejemplo:
1 Cambie las posiciones de los elementos en la diagonal principal de 2 x 2. Si su matriz es 2 x 2, puede usar un atajo para hacer este cálculo mucho más fácil.[7] El primer paso en este acceso directo implica cambiar el elemento superior izquierdo con el elemento inferior derecho. Por ejemplo:  2 Tome el opuesto de los otros dos elementos, pero déjelos en posición. En otras palabras, multiplicar la parte superior derecho y abajo izquierda elementos por -1:
2 Tome el opuesto de los otros dos elementos, pero déjelos en posición. En otras palabras, multiplicar la parte superior derecho y abajo izquierda elementos por -1: 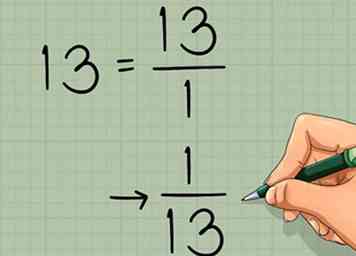 3 Toma el recíproco del determinante. Encontró el determinante de esta matriz en la sección anterior, por lo que no es necesario calcularla por segunda vez. Simplemente escriba el 1 / (determinante) recíproco:
3 Toma el recíproco del determinante. Encontró el determinante de esta matriz en la sección anterior, por lo que no es necesario calcularla por segunda vez. Simplemente escriba el 1 / (determinante) recíproco: 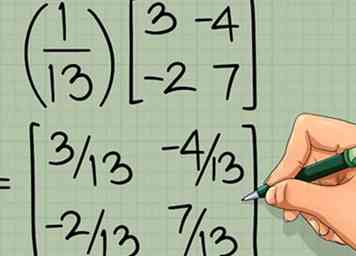 4 Multiplica la nueva matriz por el recíproco del determinante. Multiplica cada elemento de la nueva matriz por el recíproco que acabas de encontrar. La matriz resultante es la inversa de la matriz 2 x 2:
4 Multiplica la nueva matriz por el recíproco del determinante. Multiplica cada elemento de la nueva matriz por el recíproco que acabas de encontrar. La matriz resultante es la inversa de la matriz 2 x 2: 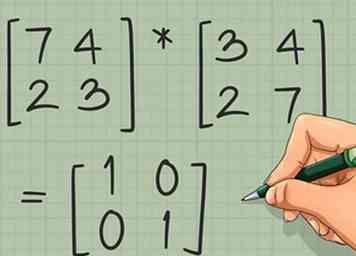 5 Confirma que el inverso es correcto. Para verificar tu trabajo, multiplica el inverso por la matriz original. Si el inverso es correcto, su producto siempre será la matriz de identidad,
5 Confirma que el inverso es correcto. Para verificar tu trabajo, multiplica el inverso por la matriz original. Si el inverso es correcto, su producto siempre será la matriz de identidad,  6 Revise la inversión de la matriz para matrices de 3 x 3 o más. A menos que esté aprendiendo este proceso por primera vez, ahorre tiempo usando una calculadora gráfica o software matemático para matrices más grandes. Si necesita calcularlo a mano, aquí hay un resumen rápido de un método:[9][10]
6 Revise la inversión de la matriz para matrices de 3 x 3 o más. A menos que esté aprendiendo este proceso por primera vez, ahorre tiempo usando una calculadora gráfica o software matemático para matrices más grandes. Si necesita calcularlo a mano, aquí hay un resumen rápido de un método:[9][10] 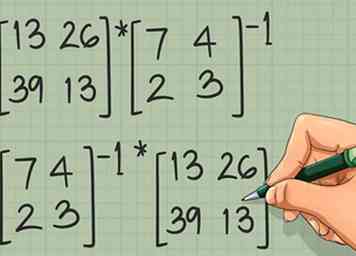 1 Escribe ambas ecuaciones posibles. En "matemáticas ordinarias" con cantidades escalares, la multiplicación es conmutativa; 2 x 6 = 6 x 2. Esto no es cierto para las matrices, por lo que puede necesitar resolver dos problemas:
1 Escribe ambas ecuaciones posibles. En "matemáticas ordinarias" con cantidades escalares, la multiplicación es conmutativa; 2 x 6 = 6 x 2. Esto no es cierto para las matrices, por lo que puede necesitar resolver dos problemas: 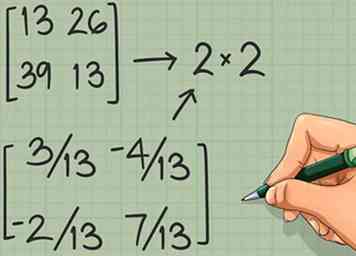 2 Encuentra las dimensiones de tu respuesta. Las dimensiones de la matriz final son las dimensiones externas de los dos factores. Tiene el mismo número de filas que la primera matriz y el mismo número de columnas que la segunda matriz.
2 Encuentra las dimensiones de tu respuesta. Las dimensiones de la matriz final son las dimensiones externas de los dos factores. Tiene el mismo número de filas que la primera matriz y el mismo número de columnas que la segunda matriz. 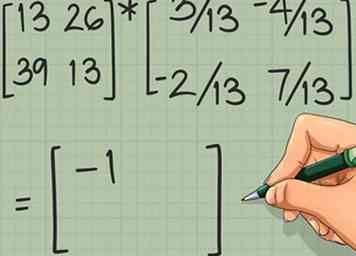 3 Encuentra el valor del primer elemento. Consulte el artículo vinculado para obtener instrucciones completas o actualice su memoria con este resumen:
3 Encuentra el valor del primer elemento. Consulte el artículo vinculado para obtener instrucciones completas o actualice su memoria con este resumen:  4 Repita el proceso del producto escalar para cada posición en su matriz. Por ejemplo, el elemento en la posición 2,1 es el producto escalar de [A] fila 2 y [B]-1 columna 1. Trate de completar el ejemplo por su cuenta. Deberías obtener las siguientes respuestas:
4 Repita el proceso del producto escalar para cada posición en su matriz. Por ejemplo, el elemento en la posición 2,1 es el producto escalar de [A] fila 2 y [B]-1 columna 1. Trate de completar el ejemplo por su cuenta. Deberías obtener las siguientes respuestas: