Minotauromaquia
Un vector es un objeto geométrico que tiene dirección y magnitud. Puede representarse como un segmento de línea con un punto inicial (punto de inicio) en un extremo y una flecha en el otro extremo, de modo que la longitud del segmento de línea sea la magnitud del vector y la flecha indique la dirección del vector . La normalización de vectores es un ejercicio común en matemáticas y también tiene aplicaciones prácticas en gráficos por computadora.
Método uno de cinco:
Definir términos
-
1 Definir un vector de unidad. El vector unitario de un vector A es el vector con el mismo punto inicial y dirección que A, pero con una longitud de 1 unidad. Se puede demostrar matemáticamente que hay un solo vector unitario para cada vector dado A. -
2 Definir la normalización de un vector. Este es el proceso de identificación del vector unitario para un vector dado A. -
3 Definir un vector ligado Un vector vinculado en el espacio cartesiano tiene su punto inicial en el origen del sistema de coordenadas, expresado como (0,0) en dos dimensiones. Esto le permite identificar un vector únicamente en términos de su punto terminal. -
4 Describe la notación vectorial Al restringirnos a vectores vinculados, A = (x, y) donde el par de coordenadas (x, y) indica la ubicación del punto terminal para el vector A.
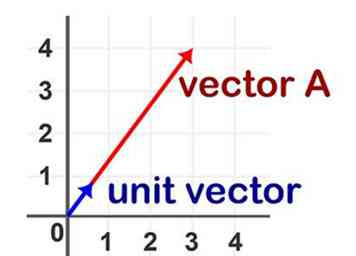1 Definir un vector de unidad. El vector unitario de un vector A es el vector con el mismo punto inicial y dirección que A, pero con una longitud de 1 unidad. Se puede demostrar matemáticamente que hay un solo vector unitario para cada vector dado A. 
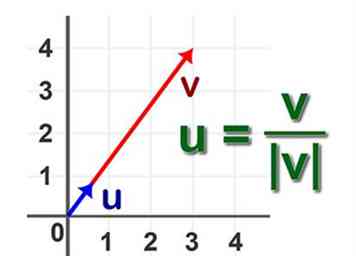2 Definir la normalización de un vector. Este es el proceso de identificación del vector unitario para un vector dado A. 
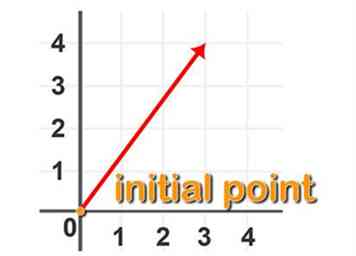3 Definir un vector ligado Un vector vinculado en el espacio cartesiano tiene su punto inicial en el origen del sistema de coordenadas, expresado como (0,0) en dos dimensiones. Esto le permite identificar un vector únicamente en términos de su punto terminal. 
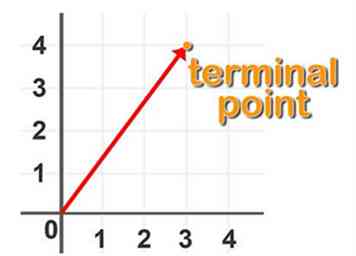4 Describe la notación vectorial Al restringirnos a vectores vinculados, A = (x, y) donde el par de coordenadas (x, y) indica la ubicación del punto terminal para el vector A. Método dos de cinco:
Analiza el objetivo
-
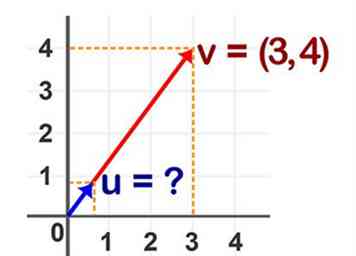1 Establezca los valores conocidos. A partir de la definición del vector unitario, sabemos que el punto inicial y la dirección del vector unitario es el mismo que el vector A. Además, sabemos que la longitud del vector unitario es 1. -
2 Determine el valor desconocido. La única variable que necesitamos calcular es el punto terminal del vector unitario.
1 Establezca los valores conocidos. A partir de la definición del vector unitario, sabemos que el punto inicial y la dirección del vector unitario es el mismo que el vector A. Además, sabemos que la longitud del vector unitario es 1. 
2 Determine el valor desconocido. La única variable que necesitamos calcular es el punto terminal del vector unitario. Método tres de cinco:
Derive una solución para el Vector de la unidad
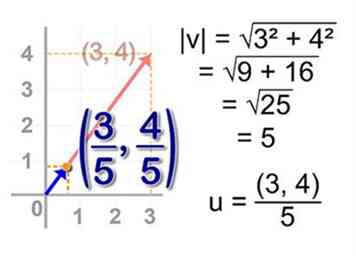
- Encuentre el punto terminal para el vector unitario del vector A = (x, y). A partir de la proporcionalidad de triángulos similares, usted sabe que cualquier vector que tenga la misma dirección que el vector A tendrá un punto terminal (x / c, y / c) para algunos c. Además, usted sabe que la longitud del vector unitario es 1. Por lo tanto, según el Teorema de Pitágoras, [x ^ 2 / c ^ 2 + y ^ 2 / c ^ 2] ^ (1/2) = 1 -> [(x ^ 2 + y ^ 2) / c ^ 2] ^ (1/2) -> (x ^ 2 + y ^ 2) ^ (1/2) / c = 1 -> c = (x ^ 2 + y ^ 2) ^ (1/2). Por lo tanto, el vector unitario u para el vector A = (x, y) se da como u = (x / (x ^ 2 + y ^ 2) ^ (1/2), y / (x ^ 2 + y ^ 2 ) ^ (1/2))
Método cuatro de cinco:
Normalizar un vector en 2 espacios dimensionales
- Deje que el vector A sea un vector con su punto inicial en el punto de origen y terminal en (2,3), tal que A = (2,3). Calcula el vector unitario u = (x / (x ^ 2 + y ^ 2) ^ (1/2), y / (x ^ 2 + y ^ 2) ^ (1/2)) = (2 / (2 ^ 2 + 3 ^ 2) ^ (1/2), 3 / (2 ^ 2 + 3 ^ 2) ^ (1/2)) = (2 / (13 ^ (1/2)), 3 / (13 ^ (1/2))). Por lo tanto, A = (2,3) se normaliza a u = (2 / (13 ^ (1/2)), 3 / (13 ^ (1/2))).
Método cinco de cinco:
Normalizar un vector en n espacio dimensional
- Generalice la ecuación para la normalización del vector en el espacio de cualquier dimensión. Un vector A (a, b, c, ...), u = (a / z, b / z, c / z, ...) donde z = (a ^ 2 + b ^ 2 + c ^ 2 ...) ^ (1 / 2).