En estadística, el modo de un conjunto de números es el número que aparece con mayor frecuencia en el conjunto. Un conjunto de datos no necesariamente tiene que tener solo un modo: si dos o más valores están "atados" por ser los más comunes, se puede decir que el conjunto es bimodal o multimodal, respectivamente, en otras palabras, todos los valores más comunes son los modos del conjunto. Para obtener una visión detallada del proceso de determinación de los modos de un conjunto de datos, consulte el Paso 1 a continuación para comenzar.
Método uno de dos:
Encontrar el modo de un conjunto de datos
-
 1 Escriba los números en su conjunto de datos. Los modos generalmente se toman de conjuntos de puntos de datos estadísticos o listas de valores numéricos. Por lo tanto, para encontrar un modo, necesitarás un conjunto de datos para encontrarlo. Es difícil hacer cálculos de modo mentalmente para todos, excepto para el conjunto de datos más pequeño, por lo que, en la mayoría de los casos, es aconsejable comenzar escribiendo (o escribiendo) su conjunto de datos. Si está trabajando con papel y lápiz, bastará con escribir los valores de su conjunto de datos en secuencia, mientras que si está usando una computadora, puede usar un programa de hoja de cálculo para agilizar el proceso.
1 Escriba los números en su conjunto de datos. Los modos generalmente se toman de conjuntos de puntos de datos estadísticos o listas de valores numéricos. Por lo tanto, para encontrar un modo, necesitarás un conjunto de datos para encontrarlo. Es difícil hacer cálculos de modo mentalmente para todos, excepto para el conjunto de datos más pequeño, por lo que, en la mayoría de los casos, es aconsejable comenzar escribiendo (o escribiendo) su conjunto de datos. Si está trabajando con papel y lápiz, bastará con escribir los valores de su conjunto de datos en secuencia, mientras que si está usando una computadora, puede usar un programa de hoja de cálculo para agilizar el proceso. - El proceso de búsqueda de un modo de conjunto de datos es más fácil de entender siguiendo junto con un problema de ejemplo. En esta sección, usemos este conjunto de valores para los propósitos de nuestro ejemplo: 18, 21, 11, 21, 15, 19, 17, 21, 17. En los próximos pasos, encontraremos el modo de este conjunto.
-
 2 Ordene los números del más pequeño al más grande. A continuación, a menudo es una buena idea ordenar los valores de su conjunto de datos para que estén en orden ascendente. Aunque esto no es estrictamente necesario, facilita el proceso de búsqueda del modo porque agrupa valores idénticos uno al lado del otro. Para grandes conjuntos de datos, puede ser prácticamente una necesidad, ya que clasificar las largas listas de valores y mantener los recuentos mentales de cuántas veces aparece cada número en la lista es difícil y puede conducir a errores.
2 Ordene los números del más pequeño al más grande. A continuación, a menudo es una buena idea ordenar los valores de su conjunto de datos para que estén en orden ascendente. Aunque esto no es estrictamente necesario, facilita el proceso de búsqueda del modo porque agrupa valores idénticos uno al lado del otro. Para grandes conjuntos de datos, puede ser prácticamente una necesidad, ya que clasificar las largas listas de valores y mantener los recuentos mentales de cuántas veces aparece cada número en la lista es difícil y puede conducir a errores. - Si trabajas con papel y lápiz, volver a escribir puede ahorrar tiempo a largo plazo. Escanee el conjunto de números para el número más bajo y, cuando lo encuentre, márquelo en el primer conjunto de datos y vuelva a escribirlo en su nuevo conjunto de datos. Repita para el segundo número más bajo, el tercero más bajo, y así sucesivamente, asegurándose de escribir cada número tantas veces como ocurra en el conjunto de datos original.
- Con una computadora, sus opciones son más amplias; por ejemplo, la mayoría de los programas de hoja de cálculo tendrán la opción de reordenar listas de valores de menor a mayor con solo unos pocos clics.
- En nuestro ejemplo, después de reordenar, la nueva lista de valores debe leer: 11, 15, 17, 17, 18, 19, 21, 21, 21.
-
 3 Cuente el número de veces que se repite cada número. A continuación, cuente el número de veces que aparece cada número en el conjunto. Busque el valor que ocurre más comúnmente en el conjunto de datos. Para conjuntos de datos relativamente pequeños con puntos ordenados en orden ascendente, esto generalmente es una simple cuestión de encontrar el mayor "grupo" de valores idénticos y contar el número de ocurrencias.
3 Cuente el número de veces que se repite cada número. A continuación, cuente el número de veces que aparece cada número en el conjunto. Busque el valor que ocurre más comúnmente en el conjunto de datos. Para conjuntos de datos relativamente pequeños con puntos ordenados en orden ascendente, esto generalmente es una simple cuestión de encontrar el mayor "grupo" de valores idénticos y contar el número de ocurrencias. - Si está trabajando con un lápiz y papel, para realizar un seguimiento de sus conteos, intente escribir la cantidad de veces que cada valor aparece sobre cada grupo de números idénticos. Si está utilizando un programa de hoja de cálculo en una computadora, puede hacer lo mismo escribiendo sus totales en celdas adyacentes o, alternativamente, usando una de las opciones del programa para el recuento de puntos de datos.
- En nuestro ejemplo, (11, 15, 17, 17, 18, 19, 21, 21, 21), 11 ocurre una vez, 15 ocurre una vez, 17 ocurre dos veces, 18 ocurre una vez, 19 ocurre una vez y 21 ocurre tres veces. 21 es el valor más común en este conjunto de datos.
-
 4 Identifique el valor (o valores) que ocurren con mayor frecuencia. Cuando sepa cuántas veces se produce cada valor en su conjunto de datos, encuentre el valor que ocurre la mayor cantidad de veces. Este es el modo de su conjunto de datos. Tenga en cuenta que puede haber más de un modo en un conjunto de datos. Si los dos valores están vinculados por ser los valores más comunes en el conjunto, se puede decir que el conjunto de datos es bimodal, mientras que si tres valores están vinculados, el conjunto es trimodal, y así.
4 Identifique el valor (o valores) que ocurren con mayor frecuencia. Cuando sepa cuántas veces se produce cada valor en su conjunto de datos, encuentre el valor que ocurre la mayor cantidad de veces. Este es el modo de su conjunto de datos. Tenga en cuenta que puede haber más de un modo en un conjunto de datos. Si los dos valores están vinculados por ser los valores más comunes en el conjunto, se puede decir que el conjunto de datos es bimodal, mientras que si tres valores están vinculados, el conjunto es trimodal, y así. - En nuestro conjunto de ejemplos, (11, 15, 17, 17, 18, 19, 21, 21, 21), porque 21 ocurre más veces que cualquier otro valor, 21 es el modo.
- Si un valor además de 21 tenía además ocurrieron tres veces (como, por ejemplo, si había uno más 17 en el conjunto de datos), 21 y este otro número ambos ser el modo.
-
 5 No confunda el modo de un conjunto de datos con su media o mediana. Tres conceptos estadísticos que a menudo se discuten juntos son los medios, las medianas y los modos. Debido a que todos estos conceptos tienen nombres que suenan similares y porque, para un solo conjunto de datos, un único valor a veces puede ser más de uno de estas cosas, es fácil confundirlos. Sin embargo, independientemente de si el modo del conjunto de datos es o no es mediana o mala, es importante comprender que estos tres conceptos son completamente independientes entre sí. Vea abajo:
5 No confunda el modo de un conjunto de datos con su media o mediana. Tres conceptos estadísticos que a menudo se discuten juntos son los medios, las medianas y los modos. Debido a que todos estos conceptos tienen nombres que suenan similares y porque, para un solo conjunto de datos, un único valor a veces puede ser más de uno de estas cosas, es fácil confundirlos. Sin embargo, independientemente de si el modo del conjunto de datos es o no es mediana o mala, es importante comprender que estos tres conceptos son completamente independientes entre sí. Vea abajo: - Un conjunto de datos media es su promedio Para encontrar la media, sume todos los valores en el conjunto de datos, luego divida por el número de valores en el conjunto. Por ejemplo, para nuestro conjunto de datos de ejemplo (11, 15, 17, 17, 18, 19, 21, 21, 21), la media sería 11 + 15 + 17 + 17 + 18 + 19 + 21 + 21 + 21 = 160/9 = 17.78. Tenga en cuenta que dividimos la suma de los valores por 9 porque hay un total de 9 valores en el conjunto de datos.

- Un conjunto de datos mediana es el "número medio" que separa los valores más bajos y más altos de un conjunto de datos en dos mitades iguales. Por ejemplo, en nuestro conjunto de datos de ejemplo, (11, 15, 17, 17, 18, 19, 21, 21, 21) 18 es la mediana porque es el número del medio; hay exactamente cuatro números más altos que él y cuatro números más bajos que él.Tenga en cuenta que si hay un número par de valores en el conjunto de datos, no hay una sola mediana. En estos casos, la mediana generalmente se toma como la media de los dos números medios.

- Un conjunto de datos media es su promedio Para encontrar la media, sume todos los valores en el conjunto de datos, luego divida por el número de valores en el conjunto. Por ejemplo, para nuestro conjunto de datos de ejemplo (11, 15, 17, 17, 18, 19, 21, 21, 21), la media sería 11 + 15 + 17 + 17 + 18 + 19 + 21 + 21 + 21 = 160/9 = 17.78. Tenga en cuenta que dividimos la suma de los valores por 9 porque hay un total de 9 valores en el conjunto de datos.
Método dos de dos:
Encontrar el modo en casos especiales
-
 1 Reconozca que no existe modo para los conjuntos de datos en los que cada valor ocurre el mismo número de veces. Si los valores en un conjunto dado ocurren todos el mismo número de veces, el conjunto de datos no tiene modo porque ningún número es más común que cualquier otro. Por ejemplo, los conjuntos de datos en los que cada valor se produce una vez no tienen modo. Lo mismo es cierto para los conjuntos de datos en los que cada valor ocurre dos veces, tres veces, y así sucesivamente.
1 Reconozca que no existe modo para los conjuntos de datos en los que cada valor ocurre el mismo número de veces. Si los valores en un conjunto dado ocurren todos el mismo número de veces, el conjunto de datos no tiene modo porque ningún número es más común que cualquier otro. Por ejemplo, los conjuntos de datos en los que cada valor se produce una vez no tienen modo. Lo mismo es cierto para los conjuntos de datos en los que cada valor ocurre dos veces, tres veces, y así sucesivamente. - Si cambiamos nuestro conjunto de datos de ejemplo a 11, 15, 17, 18, 19, 21 para que cada valor ocurra solo una vez, el conjunto de datos ahora tiene no modo. Lo mismo es cierto si cambiamos el conjunto de datos para que cada valor se produzca dos veces: 11, 11, 15, 15, 17, 17, 18, 18, 19, 19, 21, 21.
-
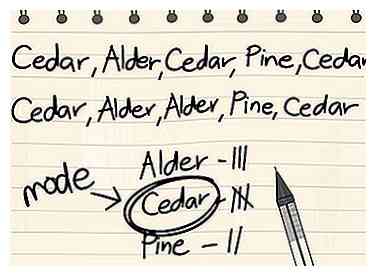 2 Reconozca que los modos para conjuntos de datos no numéricos se pueden encontrar de la misma manera que para los conjuntos de datos numéricos. En general, la mayoría de los conjuntos de datos son cuantitativo - tratan con datos en forma de números. Sin embargo, algunos conjuntos de datos tratan con datos que no se expresan en forma de números. En estos casos, se puede decir que el "modo" es el valor único que se produce más en el conjunto de datos, al igual que para los conjuntos de datos numéricos.[1] En estos casos, puede ser posible encontrar el modo mientras que es imposible encontrar una mediana o media significativa para el conjunto de datos.
2 Reconozca que los modos para conjuntos de datos no numéricos se pueden encontrar de la misma manera que para los conjuntos de datos numéricos. En general, la mayoría de los conjuntos de datos son cuantitativo - tratan con datos en forma de números. Sin embargo, algunos conjuntos de datos tratan con datos que no se expresan en forma de números. En estos casos, se puede decir que el "modo" es el valor único que se produce más en el conjunto de datos, al igual que para los conjuntos de datos numéricos.[1] En estos casos, puede ser posible encontrar el modo mientras que es imposible encontrar una mediana o media significativa para el conjunto de datos. - Por ejemplo, digamos que una encuesta biológica determina la especie de cada árbol en una pequeña parte local. El conjunto de datos para los tipos de árboles en el parque es Cedro, Aliso, Cedro, Pino, Cedro, Cedro, Aliso, Aliso, Pino, Cedro. Este tipo de conjunto de datos se llama nominal conjunto de datos porque los puntos de datos se distinguen solo por sus nombres. En este caso, el modo del conjunto de datos es Cedro porque ocurre más a menudo (cinco veces en comparación con tres para Alder y dos para Pine).
- Tenga en cuenta que, para el conjunto de datos de ejemplo anterior, es imposible calcular una media o mediana porque los puntos de datos no tienen valor numérico.
-
 3 Reconozca que para las distribuciones simétricas unimodales, el modo, la media y la mediana coinciden. Como se señaló anteriormente, es posible que el modo, la mediana y / o la media se superpongan en ciertos casos. En casos especiales, selectos donde la función de densidad del conjunto de datos forma una curva perfectamente simétrica con un modo (por ejemplo, la curva gaussiana o "forma de campana"), el modo, la media y la mediana tendrán el mismo valor. Debido a que una función de distribución representa la ocurrencia relativa de los puntos de datos, el modo estará naturalmente en el medio exacto de una curva de distribución simétrica, ya que este es el punto más alto en el gráfico y corresponde al valor más común. Debido a que el conjunto de datos es simétrico, este punto en el gráfico se corresponderá con la mediana, el valor medio en el conjunto de datos y la media, el promedio del conjunto de datos.
3 Reconozca que para las distribuciones simétricas unimodales, el modo, la media y la mediana coinciden. Como se señaló anteriormente, es posible que el modo, la mediana y / o la media se superpongan en ciertos casos. En casos especiales, selectos donde la función de densidad del conjunto de datos forma una curva perfectamente simétrica con un modo (por ejemplo, la curva gaussiana o "forma de campana"), el modo, la media y la mediana tendrán el mismo valor. Debido a que una función de distribución representa la ocurrencia relativa de los puntos de datos, el modo estará naturalmente en el medio exacto de una curva de distribución simétrica, ya que este es el punto más alto en el gráfico y corresponde al valor más común. Debido a que el conjunto de datos es simétrico, este punto en el gráfico se corresponderá con la mediana, el valor medio en el conjunto de datos y la media, el promedio del conjunto de datos. - Por ejemplo, consideremos el conjunto de datos 1, 2, 2, 3, 3, 3, 4, 4, 5. Si tuviéramos que graficar la distribución de este conjunto de datos, obtendríamos una curva simétrica que alcanza una altura de 3 en x = 3 y se reduce a una altura de 1 en x = 1 y x = 5. Porque 3 es el valor más común, es el modo. Debido a que el 3 central en el conjunto de datos tiene 4 valores a cada lado, 3 es también la mediana. Finalmente, el promedio del conjunto de datos es de 1 + 2 + 2 + 3 + 3 + 3 + 4 + 4 + 5 = 27/9 = 3, lo que significa que 3 es también el significado.
- La excepción a esta regla es para conjuntos de datos simétricos con más de un modo; en este caso, debido a que solo puede haber una mediana y media para el conjunto de datos, ambos modos no coincidirán con estos otros puntos.
 Minotauromaquia
Minotauromaquia
 1 Escriba los números en su conjunto de datos. Los modos generalmente se toman de conjuntos de puntos de datos estadísticos o listas de valores numéricos. Por lo tanto, para encontrar un modo, necesitarás un conjunto de datos para encontrarlo. Es difícil hacer cálculos de modo mentalmente para todos, excepto para el conjunto de datos más pequeño, por lo que, en la mayoría de los casos, es aconsejable comenzar escribiendo (o escribiendo) su conjunto de datos. Si está trabajando con papel y lápiz, bastará con escribir los valores de su conjunto de datos en secuencia, mientras que si está usando una computadora, puede usar un programa de hoja de cálculo para agilizar el proceso.
1 Escriba los números en su conjunto de datos. Los modos generalmente se toman de conjuntos de puntos de datos estadísticos o listas de valores numéricos. Por lo tanto, para encontrar un modo, necesitarás un conjunto de datos para encontrarlo. Es difícil hacer cálculos de modo mentalmente para todos, excepto para el conjunto de datos más pequeño, por lo que, en la mayoría de los casos, es aconsejable comenzar escribiendo (o escribiendo) su conjunto de datos. Si está trabajando con papel y lápiz, bastará con escribir los valores de su conjunto de datos en secuencia, mientras que si está usando una computadora, puede usar un programa de hoja de cálculo para agilizar el proceso.  2 Ordene los números del más pequeño al más grande. A continuación, a menudo es una buena idea ordenar los valores de su conjunto de datos para que estén en orden ascendente. Aunque esto no es estrictamente necesario, facilita el proceso de búsqueda del modo porque agrupa valores idénticos uno al lado del otro. Para grandes conjuntos de datos, puede ser prácticamente una necesidad, ya que clasificar las largas listas de valores y mantener los recuentos mentales de cuántas veces aparece cada número en la lista es difícil y puede conducir a errores.
2 Ordene los números del más pequeño al más grande. A continuación, a menudo es una buena idea ordenar los valores de su conjunto de datos para que estén en orden ascendente. Aunque esto no es estrictamente necesario, facilita el proceso de búsqueda del modo porque agrupa valores idénticos uno al lado del otro. Para grandes conjuntos de datos, puede ser prácticamente una necesidad, ya que clasificar las largas listas de valores y mantener los recuentos mentales de cuántas veces aparece cada número en la lista es difícil y puede conducir a errores.  3 Cuente el número de veces que se repite cada número. A continuación, cuente el número de veces que aparece cada número en el conjunto. Busque el valor que ocurre más comúnmente en el conjunto de datos. Para conjuntos de datos relativamente pequeños con puntos ordenados en orden ascendente, esto generalmente es una simple cuestión de encontrar el mayor "grupo" de valores idénticos y contar el número de ocurrencias.
3 Cuente el número de veces que se repite cada número. A continuación, cuente el número de veces que aparece cada número en el conjunto. Busque el valor que ocurre más comúnmente en el conjunto de datos. Para conjuntos de datos relativamente pequeños con puntos ordenados en orden ascendente, esto generalmente es una simple cuestión de encontrar el mayor "grupo" de valores idénticos y contar el número de ocurrencias.  4 Identifique el valor (o valores) que ocurren con mayor frecuencia. Cuando sepa cuántas veces se produce cada valor en su conjunto de datos, encuentre el valor que ocurre la mayor cantidad de veces. Este es el modo de su conjunto de datos. Tenga en cuenta que puede haber más de un modo en un conjunto de datos. Si los dos valores están vinculados por ser los valores más comunes en el conjunto, se puede decir que el conjunto de datos es bimodal, mientras que si tres valores están vinculados, el conjunto es trimodal, y así.
4 Identifique el valor (o valores) que ocurren con mayor frecuencia. Cuando sepa cuántas veces se produce cada valor en su conjunto de datos, encuentre el valor que ocurre la mayor cantidad de veces. Este es el modo de su conjunto de datos. Tenga en cuenta que puede haber más de un modo en un conjunto de datos. Si los dos valores están vinculados por ser los valores más comunes en el conjunto, se puede decir que el conjunto de datos es bimodal, mientras que si tres valores están vinculados, el conjunto es trimodal, y así.  5 No confunda el modo de un conjunto de datos con su media o mediana. Tres conceptos estadísticos que a menudo se discuten juntos son los medios, las medianas y los modos. Debido a que todos estos conceptos tienen nombres que suenan similares y porque, para un solo conjunto de datos, un único valor a veces puede ser más de uno de estas cosas, es fácil confundirlos. Sin embargo, independientemente de si el modo del conjunto de datos es o no es mediana o mala, es importante comprender que estos tres conceptos son completamente independientes entre sí. Vea abajo:
5 No confunda el modo de un conjunto de datos con su media o mediana. Tres conceptos estadísticos que a menudo se discuten juntos son los medios, las medianas y los modos. Debido a que todos estos conceptos tienen nombres que suenan similares y porque, para un solo conjunto de datos, un único valor a veces puede ser más de uno de estas cosas, es fácil confundirlos. Sin embargo, independientemente de si el modo del conjunto de datos es o no es mediana o mala, es importante comprender que estos tres conceptos son completamente independientes entre sí. Vea abajo: 

 1 Reconozca que no existe modo para los conjuntos de datos en los que cada valor ocurre el mismo número de veces. Si los valores en un conjunto dado ocurren todos el mismo número de veces, el conjunto de datos no tiene modo porque ningún número es más común que cualquier otro. Por ejemplo, los conjuntos de datos en los que cada valor se produce una vez no tienen modo. Lo mismo es cierto para los conjuntos de datos en los que cada valor ocurre dos veces, tres veces, y así sucesivamente.
1 Reconozca que no existe modo para los conjuntos de datos en los que cada valor ocurre el mismo número de veces. Si los valores en un conjunto dado ocurren todos el mismo número de veces, el conjunto de datos no tiene modo porque ningún número es más común que cualquier otro. Por ejemplo, los conjuntos de datos en los que cada valor se produce una vez no tienen modo. Lo mismo es cierto para los conjuntos de datos en los que cada valor ocurre dos veces, tres veces, y así sucesivamente.  2 Reconozca que los modos para conjuntos de datos no numéricos se pueden encontrar de la misma manera que para los conjuntos de datos numéricos. En general, la mayoría de los conjuntos de datos son cuantitativo - tratan con datos en forma de números. Sin embargo, algunos conjuntos de datos tratan con datos que no se expresan en forma de números. En estos casos, se puede decir que el "modo" es el valor único que se produce más en el conjunto de datos, al igual que para los conjuntos de datos numéricos.[1] En estos casos, puede ser posible encontrar el modo mientras que es imposible encontrar una mediana o media significativa para el conjunto de datos.
2 Reconozca que los modos para conjuntos de datos no numéricos se pueden encontrar de la misma manera que para los conjuntos de datos numéricos. En general, la mayoría de los conjuntos de datos son cuantitativo - tratan con datos en forma de números. Sin embargo, algunos conjuntos de datos tratan con datos que no se expresan en forma de números. En estos casos, se puede decir que el "modo" es el valor único que se produce más en el conjunto de datos, al igual que para los conjuntos de datos numéricos.[1] En estos casos, puede ser posible encontrar el modo mientras que es imposible encontrar una mediana o media significativa para el conjunto de datos.  3 Reconozca que para las distribuciones simétricas unimodales, el modo, la media y la mediana coinciden. Como se señaló anteriormente, es posible que el modo, la mediana y / o la media se superpongan en ciertos casos. En casos especiales, selectos donde la función de densidad del conjunto de datos forma una curva perfectamente simétrica con un modo (por ejemplo, la curva gaussiana o "forma de campana"), el modo, la media y la mediana tendrán el mismo valor. Debido a que una función de distribución representa la ocurrencia relativa de los puntos de datos, el modo estará naturalmente en el medio exacto de una curva de distribución simétrica, ya que este es el punto más alto en el gráfico y corresponde al valor más común. Debido a que el conjunto de datos es simétrico, este punto en el gráfico se corresponderá con la mediana, el valor medio en el conjunto de datos y la media, el promedio del conjunto de datos.
3 Reconozca que para las distribuciones simétricas unimodales, el modo, la media y la mediana coinciden. Como se señaló anteriormente, es posible que el modo, la mediana y / o la media se superpongan en ciertos casos. En casos especiales, selectos donde la función de densidad del conjunto de datos forma una curva perfectamente simétrica con un modo (por ejemplo, la curva gaussiana o "forma de campana"), el modo, la media y la mediana tendrán el mismo valor. Debido a que una función de distribución representa la ocurrencia relativa de los puntos de datos, el modo estará naturalmente en el medio exacto de una curva de distribución simétrica, ya que este es el punto más alto en el gráfico y corresponde al valor más común. Debido a que el conjunto de datos es simétrico, este punto en el gráfico se corresponderá con la mediana, el valor medio en el conjunto de datos y la media, el promedio del conjunto de datos.